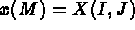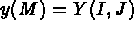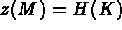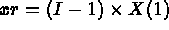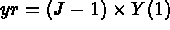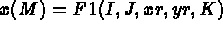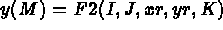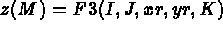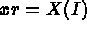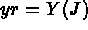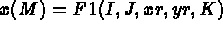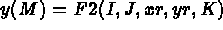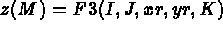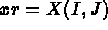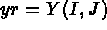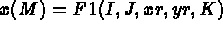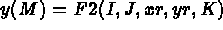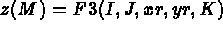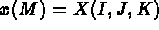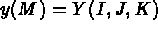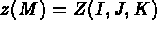




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: 3.4.4 Des exemples d'utilisation
Sup.: Méthode pour une topologie hexaédrique
Préc.: Description des données à fournir
Index
Table des matières
Les différentes options permettent de définir la géométrie, le découpage des éléments et les attributs physiques.
- La géométrie : option IOPTM, tableaux X,Y et H, fonctions F1, F2 et F3:
- IOPTM = 0 : le maillage est de type différences finies à pas constants dans les 3 directions.
X, Y et H sont trois réels (déclarés comme tableaux) qui représentent les 3
pas d'espacement dans les 3 directions. Tout point M est repéré par ses trois indices I, J et K et
aura comme coordonnées:
- IOPTM = 1 : le maillage est de type différences finies à pas variables dans les 2
premières directions et à pas constants dans la troisième.
X, Y sont deux tableaux de longueur N1 et N2, H est un réel (déclaré comme tableau), ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
- IOPTM = 2 : le maillage est de type différences finies à pas variables dans les 3
directions. X, Y et H sont trois tableaux de longueur N1, N2 et NB+1, ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
- IOPTM = 3 : le maillage est de type différences finies à pas variables dans les 2
premières directions et à pas constants dans la troisième. X, Y sont deux tableaux de longueur
N1
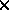 N2 et H est un réel (déclaré comme tableau), ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
N2 et H est un réel (déclaré comme tableau), ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
- IOPTM = 4 : le maillage est de type différences finies à pas variables dans les 2
premières directions et à pas variables dans la troisième. X, Y sont deux tableaux de longueur
N1
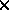 N2 et H est un tableau de longueur NB+1, ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
N2 et H est un tableau de longueur NB+1, ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
- IOPTM = 5 : un maillage de type différences finies à pas constants dans les 2
premières directions sert à construire le maillage final via la définition des points grâce aux
fonctions F1, F2 et F3. X, Y sont deux réels (déclarés comme tableau) et on obtient la construction
suivante:
et
- IOPTM = 6 : un maillage de type différences finies à pas variables dans les 2
premières directions sert à construire le maillage final via la définition des points grâce aux
fonctions F1, F2 et F3. X, Y sont deux tableaux de longueur N1 et N2 et on obtient la construction
suivante:
et
- IOPTM = 7 : un maillage de type différences finies à pas variables dans les 2
premières directions sert à construire le maillage final via la définition des points grâce aux
fonctions F1, F2 et F3. X, Y sont deux tableaux de longueur N1xN2 et on obtient la construction
suivante:
et
- IOPTM = < 0 : un maillage de type différences finies à pas variables dans les 3
directions sert à construire le maillage final via la définition des points grâce aux
tableaux à 3 indices X, Y et H (sans vérification):
- Le découpage des éléments : option NOPTDE:
- NOPTDE = 0 : le résultat est composé des hexaèdres logiquement formés
- NOPTDE = 1 : chaque hexaèdre est découpé en 2 pentaèdres suivant la direction
de la première bissectrice du plan z=0.
- NOPTDE = 2 : chaque hexaèdre est découpé en 2 pentaèdres suivant la direction
de l'autre diagonale.
- NOPTDE = 3 : on suit d'abord le cas NOPTDE = 1 puis chaque pentaèdre est découpé en
3 tétraèdres.
- NOPTDE = 4 : idem avec le choix NOPTDE = 2
- NOPTDE = 5 : chaque hexaèdre est découpé en 5 tétraèdres
- Les attributs physiques : sous-domaines et références:
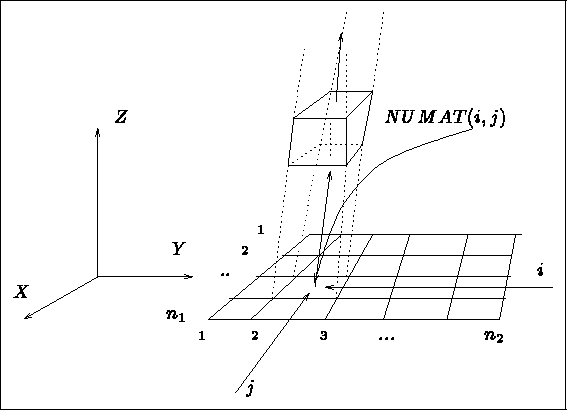
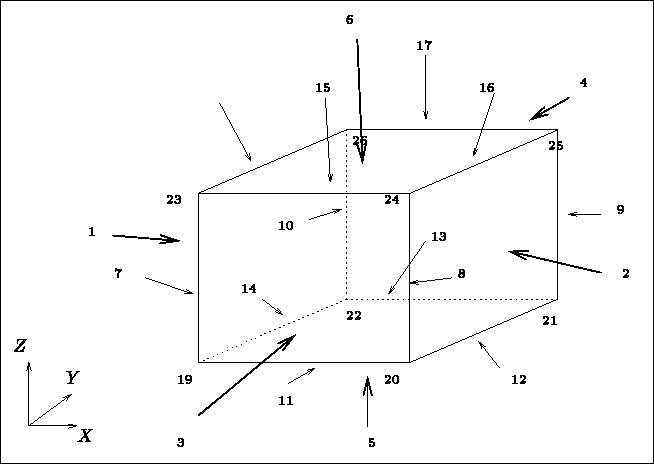
La numérotation des points est effectuée selon les indications portées sur la figure 3.30.
Celle des éléments est faite de façon analogue, couche par couche.
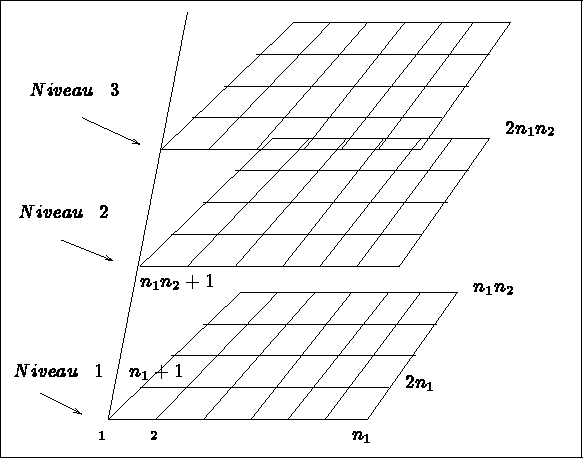
Figure: Numérotation des points par le module GEL3D1
Pour appeler le module GEL3D1 , il est nécessaire d'écrire un programme principal de la manière suivante:
- dimensionner le tableau M (dans le common blanc)
- déclarer le tableau entier NUMAT(.), tableau à 2 ou 3 indices selon les cas
- déclarer le tableau entier ITYP(NB) où NB est le nombre de couches
- déclarer le tableau réel X(.), tableau à 1, 2 ou 3 indices selon les cas
- déclarer de même les tableaux réels Y(.) et H(.)
- déclarer les externals F1, F2 et F3 (selon les cas)
- appeler INITI
appel du module
CALL GEL3D1 (M,IOPTM,JOPTSD,NOPTDE,N1,N2,NB,X,Y,H,
. F1,F2,F3,NUMAT,ITYP,NFNOPO,NINOPO,NFAUX)
avec :
- M : le super-tableau
- IOPTM : l'option de description des données
- JOPTSD : l'option de numérotation des sous-domaines
- NOPTDE : l'option de découpage des éléments
- N1 : le nombre de points dans la direction x
- N2 : le nombre de points dans la direction y
- NB : le nombre de couches (i.e. le nombre de points -1 dans la direction z)
- X,Y et H : les tableaux à 1, 2 ou 3 indices pour définir les coordonnées des points
- F1, F2 et F3 : les noms des 3 fonctions externes à fournir (selon la valeur de IOPTM) pour définir
les coordonnées des points. Ces fonctions sont de la forme suivante:
- F1(I,J,XR,YR,K) définit l'abscisse des points à partir de I et J , la position du point du plan de définition,
XR et YR les coordonnées du point I, J et K est l'indice de section (i.e. K=1,NB+1)
- F2(I,J,XR,YR,K) à la même forme et définit l'ordonnée des points
- F3(I,J,XR,YR,K) à la même forme et définit la cote des points
- NUMAT : le tableau à 2 ou 3 indices permettant l'affectation des numéros de sous-domaine
- ITYP : le tableau déterminant le type des couches (tableau lié à NUMAT)
- NF(NI)NOPO : le numéro de support de la S.D.S. NOPO et son niveau
- NFAUX : la valeur 0
Remarque :
Pour changer les références affectées automatiquement, on pourra utiliser le module MODNOP,
le préprocesseur MODNXX ou le mot-clé NUME de APNOP3.






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: 3.4.4 Des exemples d'utilisation
Sup.: Méthode pour une topologie hexaédrique
Préc.: Description des données à fournir
Index
Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
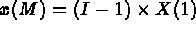
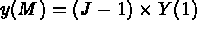
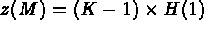
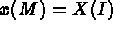
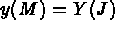
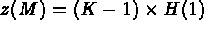
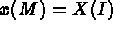
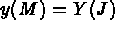
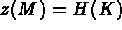
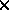 N2 et H est un réel (déclaré comme tableau), ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
N2 et H est un réel (déclaré comme tableau), ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
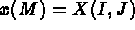
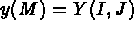
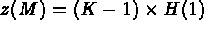
 N2 et H est un tableau de longueur NB+1, ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme:
N2 et H est un tableau de longueur NB+1, ces
valeurs permettent de trouver les coordonnées de tout point M, d'indices I, J et K comme: