Suiv.: 8 Adaptation d'un nouveau terminal Sup.: 7 Programmes internes Préc.: Aides à l'implémentation Index Table des matières

7.9 Inclassables

      REAL FUNCTION RANDOM(I)
      INTEGER I

Générateur de  nombres aléatoires 

En entrée: I < 0 initialisation du générateur (on conseille abs(I)= "grand" nombre premier)

Puis pour I 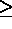0 , on obtient un nombre REAL compris entre 0 et 1.

      REAL FUNCTION ATANG(Y, X)
      REAL X, Y

C'est la  fonction ARC-TANGENTE à deux arguments mais elle ne trappe pas si X et Y valent 0., dans ce cas ATANG(0.,0.) = 0.

Le résultat est un nombre compris entre 0. et 2*PI.

Y correspond à MODULE * SIN(ALPHA)

X correspond à MODULE * COS(ALPHA)

 
      SUBROUTINE CXHULL(X, Y, CRITER, REFPTS, NBPTS, HULL, NBHULL)
      REAL X(NBPTS), Y(NBPTS)
      REAL CRITER(2, NBPTS)
      INTEGER NBPTS, REFPTS(NBPTS), HULL(NBPTS), NBHULL

Calcule l'enveloppe convexe d'un nuage de  points.

En entrée: NBPTS, X(NBPTS), Y(NBPTS) qui définissent le nuage de points et

CRITER(2, NBPTS) et REFPTS(NBPTS) les tableaux de travail pour le tri.

En sortie: HULL(NBHULL) l'enveloppe convexe de NBHULL points et

HULL: références sur X, Y définissants l'enveloppe convexe.

Les points de l'enveloppe sont donnés en tournant dans le sens positif.

      REAL FUNCTION CPXLIN(X,Y,N,HULL,NBHULL)
      INTEGER N,NBHULL,HULL(NBHULL)
      REAL X(N),Y(N)

Calcule la "complexité" du  polygone X,Y.

CPXLIN= 2*longueur de la ligne/périmètre de l'enveloppe convexe.

Entrée: X, Y ligne de N points et

HULL enveloppe convexe de NBHULL points.

Sortie: CPXLIN= 2*longueur de la ligne périmètre de l'enveloppe convexe.

      SUBROUTINE NNUEES(X, Y, Z, N, BX, BY, BZ, NBBARY, CHAINE)
      INTEGER N, NBBARY, CHAINE(N)
      REAL X(N), Y(N), Z(N), BX(NBBARY), BY(NBBARY), BZ(NBBARY)

Algorithme des  nuées dynamiques .

En entrée : N Points X, Y, Z et NBBARY barycentres initiaux BX, BY, BZ.

En sortie : les NBBARY barycentres trouvés BX, BY, BZ et

CHAINE(I) qui pointe sur le barycentre auquel le point X(I), Y(I), Z(I) appartient.

      SUBROUTINE BBLOCS(X, Y, Z, N, BX, BY, BZ, NBBARY, CHAINE)
      INTEGER N, NBBARY, CHAINE(N)
      REAL X(N), Y(N), Z(N), BX(NBBARY), BY(NBBARY), BZ(NBBARY)

En entrée : N points X, Y, Z et NBBARY le nombre de  barycentres désirés.

En sortie : les NBBARY barycentres trouvés BX, BY, BZ et

CHAINE(I) qui pointe sur le barycentre auquel le point X(I), Y(I), Z(I) appartient.

      INTEGER FUNCTION ISIGNE(I)
      INTEGER I

Renvoie 1 si I > 0, 0 si I = 0 ou -1 si I < 0