We will be interested here in binary
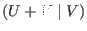 codes.
A binary
codes.
A binary
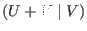 construction takes two binary codes of a same length
construction takes two binary codes of a same length 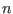 and produces a code
of length
and produces a code
of length 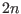 as follows (we denote here the concatenation of two vectors
as follows (we denote here the concatenation of two vectors
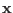 and
and
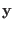 by
by
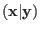 )
)
A polar code is an iterated
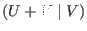 code, in the sense that the codes
code, in the sense that the codes  and
and 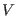 are themselves
are themselves
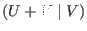 codes and so and so forth
up to the point where the constituent codes are of length
codes and so and so forth
up to the point where the constituent codes are of length  . Such codes have therefore a length which is a power of
. Such codes have therefore a length which is a power of 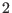 .
For instance a polar code of length
.
For instance a polar code of length 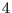 is a
is a
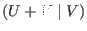 code of length
code of length 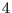 where
where
 is a code of length
is a code of length 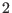 which is a
which is a
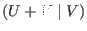 construction obtained from two codes of length
construction obtained from two codes of length  .
The same applies to the code
.
The same applies to the code 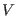 of length
of length 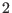 .
A polar code of length
.
A polar code of length 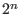 and dimension
and dimension 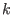 is associated in a natural way to a binary tree of depth
is associated in a natural way to a binary tree of depth 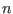 with
with 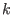 leaves corresponding
to the information bits of the code.
It is first asked to show the two properties of a
leaves corresponding
to the information bits of the code.
It is first asked to show the two properties of a
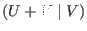 code (about their dimension and their minimum distance).
Use the property about the minimum distance and the dimension to find a polar code of length
code (about their dimension and their minimum distance).
Use the property about the minimum distance and the dimension to find a polar code of length 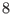 , dimension
, dimension 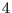 and
minimum distance
and
minimum distance 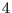 .
.
Jean-Pierre TILLICH
2019-03-08