Assume that we have a decoding algorithm for the  and the
and the 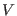 code that uses the fact that we know
for each bit
code that uses the fact that we know
for each bit  of the codeword the probability
of the codeword the probability 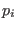 that it is equal to
that it is equal to  . Then this can be used to decode
a
. Then this can be used to decode
a
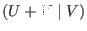 code in the following way again under the assumption that we know for each bit
code in the following way again under the assumption that we know for each bit  of
the codeword
of
the codeword
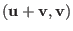 that has been sent
the probability that it is equal to
that has been sent
the probability that it is equal to  given the received symbol
given the received symbol  for it.
We number the positions of the
for it.
We number the positions of the
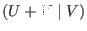 code from 0 to
code from 0 to 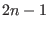 and assume that these probabilities are stored
in an array
and assume that these probabilities are stored
in an array
![$ p[0],\dots,p[2n-1]$](img31.png) . We view
. We view
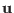 and
and
 as arrays of length
as arrays of length 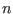 . We assume that the received
word is given by the array
. We assume that the received
word is given by the array
![$ y[0],\dots,y[2n-1]$](img33.png) .
From our assumption, we know that
.
From our assumption, we know that
We can use now the lecture on polar codes to deduce that
We can decode  by using these probabilities.
Once we know
by using these probabilities.
Once we know
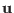 we can use the lecture on polar codes to deduce that
we can use the lecture on polar codes to deduce that
This can be used to decode the
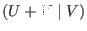 code as follows.
code as follows.

The issue is now: how can we decode  and
and 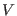 ? If
? If  and
and 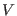 were of length
were of length  , then the
answer would be easy. For
, then the
answer would be easy. For  there are two cases to consider. Either
there are two cases to consider. Either  is the constant code, say
is the constant code, say
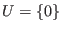 and then DecodeU would just return 0 or
and then DecodeU would just return 0 or 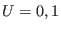 and then DecodeU
and then DecodeU
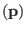 would
return 0 if
would
return 0 if
![$ p[0]<\frac{1}{2}$](img49.png) and
and  otherwise.
The recursive
otherwise.
The recursive
 structure of a polar code leads in a natural way to a recursive decoding algorithm based on these
considerations.
One uses here a table
structure of a polar code leads in a natural way to a recursive decoding algorithm based on these
considerations.
One uses here a table
![$ \mathbf{p}[0..n-1][0..2^n-1]$](img50.png) storing all the probabilities that are computed during the decoding process, where
storing all the probabilities that are computed during the decoding process, where
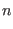 |
 |
number of layers of the polar code |
|
 |
 |
length of the polar code |
|
![$\displaystyle \mathbf{p}[n][i]$](img53.png) |
 |
 |
|
![$\displaystyle \mathbf{p}[t][i]$](img55.png) |
 |
probability  -th bit at layer -th bit at layer 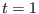 , for , for  |
|

where the auxiliary functions are defined as
![\begin{algorithmic}
\Function{UpdateU}{$i,j,t$}
\For{$l=i$\ to $j-1$}
\State{$\m...
...t+1][l])(1-2\mathbf{p}[t+1][l+2^t])}{2}$}
\EndFor
\EndFunction
\end{algorithmic}](img59.png)
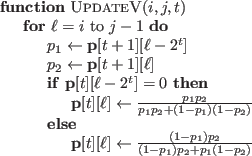
![\begin{algorithmic}
\Function{DecodeDirectly}{$i$}
\If{$\mathbf{z}[i]\neq 0$}
\S...
...
\Else { $\mathbf{p}[0][i]\gets 1$}
\EndIf
\EndIf
\EndFunction
\end{algorithmic}](img61.png)
Here
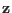 is a
table of length
is a
table of length 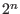 where the
where the 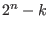 positions fixed to 0 at the beginning of the encoding process are also fixed to 0 in
positions fixed to 0 at the beginning of the encoding process are also fixed to 0 in
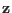 and the other
and the other 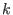 positions (where information was fed in during the encoding process) take the value
positions (where information was fed in during the encoding process) take the value 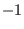 .
Decoding is performed by using the following function with the call
Decode
.
Decoding is performed by using the following function with the call
Decode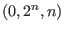 .
.
Implement this function in Java and verify that the decoding is succesful most of the time for the polar code
of length 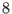 that you have found in the previous question when codewords are sent over a binary symmetric channel of crossover probability
that you have found in the previous question when codewords are sent over a binary symmetric channel of crossover probability
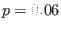 .
.
Jean-Pierre TILLICH
2019-03-08
![$\displaystyle \mathbf{prob}(u[i]=1\vert y[i],y[i+n]) = \frac{1-(1-2p[i])(1-2p[i+n])}{2}
$](img39.png)
![$\displaystyle \frac{p[i]p[i+n]}{p[i]p[i+n]+(1-p[i])(1-p[i+n])}$](img41.png) if
if ![$\displaystyle \frac{(1-p[i])p[i+n]}{(1-p[i])p[i+n]+p[i](1-p[i+n])}$](img43.png) if
if 

![\begin{algorithmic}
\Function{UpdateU}{$i,j,t$}
\For{$l=i$\ to $j-1$}
\State{$\m...
...t+1][l])(1-2\mathbf{p}[t+1][l+2^t])}{2}$}
\EndFor
\EndFunction
\end{algorithmic}](img59.png)
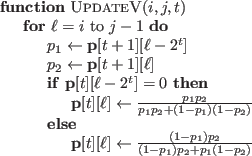
![\begin{algorithmic}
\Function{DecodeDirectly}{$i$}
\If{$\mathbf{z}[i]\neq 0$}
\S...
...
\Else { $\mathbf{p}[0][i]\gets 1$}
\EndIf
\EndIf
\EndFunction
\end{algorithmic}](img61.png)
![]() is a
table of length
is a
table of length ![]() where the
where the ![]() positions fixed to 0 at the beginning of the encoding process are also fixed to 0 in
positions fixed to 0 at the beginning of the encoding process are also fixed to 0 in
![]() and the other
and the other ![]() positions (where information was fed in during the encoding process) take the value
positions (where information was fed in during the encoding process) take the value ![]() .
Decoding is performed by using the following function with the call
Decode
.
Decoding is performed by using the following function with the call
Decode![]() .
.
![]() that you have found in the previous question when codewords are sent over a binary symmetric channel of crossover probability
that you have found in the previous question when codewords are sent over a binary symmetric channel of crossover probability
![]() .
.