Activités
de recherche
- Post-doctorat -
Je travaille
actuellement sur un modèle d'interactions entre cycle cellulaire et horloge
circadienne chez des cellules saines et cancéreuses.
Chez les mammifères,
de nombreux processus physiologiques sont contrôlés par des rythmes
moléculaires de période environ 24 heures, les rythmes circadiens (ou horloge
circadienne). Ces rythmes, bien qu'endogènes, sont très sensibles aux stimuli
extérieurs, également appelés facteurs d'entraînements exogènes ou synchroniseurs
(cycles lumière/obscurité, activité/repos, ...). Ces facteurs exogènes
modifient la période (et la phase) des rythmes circadiens afin de les faire
coïncider avec l'horloge externe dont la période est de 24 heures exactement.
Les synchroniseurs ont une action sur l'horloge moléculaire de toutes les
cellules de l'organisme et influencent donc le cycle de division de ces
dernières.
Des données issues
d'observations cliniques et d'expérimentations biologiques ont montré qu'une perturbation
des rythmes circadiens engendre une accélération de la croissance tumorale, et est
donc un facteur de mauvais pronostic pour le patient.
Ainsi, l'objectif
de ce travail est d'analyser, à l'aide de la modélisation mathématique, les interactions
entre rythmes circadiens et division cellulaire, et d'étudier in silico l'impact de ces interactions
sur la prolifération cellulaire de cellules saines et cancéreuses. Cette étude
s'intègre dans un projet européen pluridisciplinaire (C5Sys, Circadian and cell cycle
clock systems in cancer), coordonné par F. Lévi (Oncologue, Hôpital Paul
Brousse, Villejuif, INSERM U 776), et regroupant différentes équipes de
médecins, biologistes, bioinformaticiens et mathématiciens.
Mon travail est
basé sur un modèle mathématique du cycle de division cellulaire dans des
populations de cellules, modèle qui intègre un contrôle temporel de l'apoptose
et des transitions entre chacune des phases de ce cycle (G1, S, G2 et M). Ce
modèle se compose d'EDP de type von Foerster-McKendrick, régissant
l'évolution temporelle de la densité de cellules dans chacune des phases du
cycle, en fonction du temps et de l'âge des cellules dans chacune de ces
phases.
Le faible degré de
complexité du modèle favorise le recours à des données d'imagerie, par exemple
de microscopie par fluorescence telle la méthode Fucci, afin de déterminer
expérimentalement les paramètres du modèle, et plus spécifiquement les taux de
transition. Les données d'imagerie sur lesquelles mon étude est basée sont le
résultat d'une collaboration
étroite menée avec les biologistes du projet C5Sys.
La méthode Fucci
permet de déterminer, pour un temps donné, si une cellule est en phase G1 ou en
phase S/G2/M du cycle cellulaire, et donne ainsi accès à la durée passée par
cette cellule dans chacune de ces deux phases [1,2]. Développée récemment,
cette méthode ne permet pas encore de distinguer les phases S, G2 et M, d'où le
choix de se restreindre, pour le moment, à un modèle biphasique. Des données
expérimentales d'enregistrements temporels d'intensités de fluorescence ont
ainsi permis de déterminer sur une population de cellules saines in vitro, de
type NIH3T3 (fibroblastes embryonnaires de souris), non soumise à un contrôle
temporel externe (i.e. exercé par les synchroniseurs), la répartition de la durée des deux
phases, G1 et S/G2/M, au sein de la population. J'ai ajusté à ces distributions
de durées expérimentales des distributions Gamma, et ai déterminé les taux
de transition du modèle, i.e. entre les phases G1 et S/G2/M, et entre S/G2/M et
G1.
Sans contrôle
temporel (i.e. sans action d'un synchroniseur central), les oscillations des
pourcentages numériques de cellules en G1 et S/G2/M sont amorties, ce qui
reflète une désynchronisation
progressive des cellules (croissance asynchrone). L'ajout au modèle d'un
contrôle temporel 24h-périodique des transitions de phases du cycle cellulaire
induit des oscillations soutenues, 24h-périodiques, des pourcentages de
cellules en phase G1 et S/G2/M. Les cellules sont ainsi synchronisées dans le
cycle cellulaire.
Des
expérimentations réalisées dans des milieux de culture différant par leur
pourcentage de sérum foetal bovin (FBS en anglais) permettent d'étudier l'effet
de facteurs de croissance sur la synchronisation des cellules d'une même
population dans le cycle cellulaire.
Ces travaux ont
donné lieu à des publications dans différentes revues scientifiques
internationales [3,4,5,6].
Références
[1]
A. Sakaue-Sawano, H. Kurokawa, T. Morimura, A. Hanyu, H. Hama, H. Osawa, S.
Kashiwagi, K. Fukami, T. Miyata, H. Miyoshi, T. Imamura, M. Ogawa, H. Masai,
and A. Miyawaki. Visualizing spatiotemporal dynamics of
multicellular cell-cycle progression. Cell,
132(3):487–498, 2008.
[2] A. Sakaue-Sawano, K. Ohtawa, H. Hama, M. Kawano,
M. Ogawa, and A. Miyawaki. Tracing the silhouette of individual cells in S/G2/M
phases with fluorescence. Chem Biol,
15(12):1243–1248, 2008.
[3] F. Billy, J. Clairambault, O. Fercoq, S. Gaubert,
T. Lepoutre, T. Ouillon, S. Saito. Synchronisation and control of proliferation
in cycling cell population models with age structure. Math Comp Simul, 2012. 46 pages. In press.
[4] F. Billy, J. Clairambault, O. Fercoq, S. Gaubert,
T. Lepoutre, T. Ouillon. Proliferation in cell population models with age
structure. In Proceedings of ICNAAM 2011,
[5] F. Billy, J. Clairambault, and O. Fercoq.
Optimisation of cancer drug treatments using cell population dynamics. In
''Mathematical Methods and Models in Biomedicine'', pages 257-
[6] F. Billy, J. Clairambault, F. Delaunay, C.
Feillet, N. Robert. Age-structured cell population model to study the influence
of growth factors on cell cycle dynamics. Math Biosc
Eng, 2012.
17 pages. Accepted .
- Doctorat -
Mon travail de
Doctorat a consisté à développer un modèle mathématique multi-échelle de l'angiogenèse
tumorale, i.e. à établir des équations mathématiques permettant de
retranscrire les différents mécanismes considérés, à résoudre numériquement ces
équations, à déterminer la valeur des différents paramètres du modèle, et à
mener des expériences in silico.
Ce modèle se compose de douze équations aux dérivées partielles (quatre
équations stationnaires et huit non-stationnaires) de type réaction-diffusion et chemotaxie /
transport.
L'angiogenèse se
définit comme le processus de formation de nouveaux vaisseaux sanguins à partir de
vaisseaux préexistants.
L'angiogenèse joue
un rôle déterminant dans le développement des cancers. En effet, une tumeur
solide se développe initialement grâce aux ressources, oxygène et nutriments,
disponibles dans son environnement. Cependant, lorsque ces ressources
deviennent rares, la tumeur ne peut poursuivre son développement. Cette tumeur
induit alors, par sécrétion de substances chemoattractantes diffusant dans le
milieu environnant, la création de micro-vaisseaux à partir des vaisseaux
sanguins préexistants. Ces néo-vaisseaux se développent en direction de la
tumeur. Disposant ainsi de son propre réseau vasculaire, cette dernière peut,
par l'intermédiaire du flux sanguin, s'approvisionner en oxygène et nutriments,
et poursuivre ainsi son développement.
La complexité des
phénomènes impliqués dans la croissance tumorale et l'angiogenèse rend
l'élaboration et l'optimisation des traitements anti-angiogéniques difficiles
et potentiellement dangereuses pour les patients concernés. Dès lors, la
modélisation mathématique apparaît comme une approche complémentaire aux
approches biologiques traditionnelles.
Le modèle
mathématique d'angiogenèse tumorale que j'ai développé pendant mon Doctorat
intègre les principaux mécanismes intervenant au cours de l'angiogenèse
tumorale aux échelles
tissulaire et moléculaire. En effet, outre les phénomènes
tissulaires traditionnellement décrits dans les modèles disponibles dans la
littérature (diffusion, chemotaxie), mon modèle intègre les mécanismes de
liaison ligand-récepteur, mécanismes clés de la communication intercellulaire.
Ce modèle est le premier modèle d'angiogenèse à considérer les interactions
moléculaires entre différentes substances pro- et anti-angiogéniques
(endogènes ou exogènes), facteurs déterminant dans la régulation de
l'angiogenèse tumorale. Ces interactions n'étant pas prises en compte dans les
modèles d'angiogenèse précédemment développés, ces derniers ne peuvent
prétendre étudier leur rôle dans le processus angiogénique, ni, par conséquent,
modéliser l'action de traitements anti-angiogéniques de façon mécanistique.
Mon modèle est, de
plus, couplé à un modèle de croissance tumorale adapté d'un modèle de cycle
cellulaire structuré en âge développé par D. Bresch et al [7].
D'un point de vue
mathématique, ce modèle d'angiogenèse couplée à la croissance tumorale repose
sur des équations aux dérivées partielles de réaction-diffusion, chemotaxie /
transport modélisant l'évolution spatio-temporelle des densités de
cellules endothéliales (constituant la paroi des vaisseaux sanguins), de
cellules tumorales, ainsi que des concentrations tissulaires en substances
pro-angiogéniques actives (VEGF, angiopoïétine-2) et anti-angiogéniques actives
(endostatine, angiopoïétine-1), et en oxygène. J'ai distingué les cellules
endothéliales stables, i.e. constituant la paroi des vaisseaux sanguins
fonctionnels, des cellules endothéliales instables, proliférant et migrant en
direction de la tumeur. A l'échelle moléculaire, les substances angiogéniques
se liant à des récepteurs spécifiques situés sur la membrane des cellules
endothéliales, j'ai modélisé ces liaisons ligand-récepteur à l'aide de lois
pharmacologiques. Cette méthode permet de prendre en compte l'action
de substances antagonistes sur le système considéré, cette action pouvant
modifier de façon significative l'évolution du processus angiogénique. Dans les
équations du modèle, ces lois interviennent dans l'expression des taux de
prolifération, chemotaxie et stabilisation des cellules endothéliales
instables.
Afin de permettre
l'implémentation de ce modèle, les équations faisant intervenir à la fois des termes
de réaction, diffusion, et chemotaxie / transport ont été discrétisées à l'aide
d'une méthode de splitting. Les équations de diffusion ont été discrétisées par
une méthode de type volumes finis. J'ai, de plus, eu recours à une
méthode de pénalisation
afin de définir la source d'oxygène, la concentration en oxygène étant supposée
constante là où la densité de néo-vaisseaux sanguins fonctionnels est
non-nulle. Les équations de chemotaxie / transport ont, quant à elles, été
discrétisées par un schéma de type WENO (Weigthed Essentially Non-Oscillatory)
d'ordre 5 en espace et par un schéma Runge-Kutta d'ordre 3 en temps. Les systèmes
linéaires découlant de ces discrétisations ont été résolus à l'aide de l'outil PETSc.
J'ai choisi d'implémenter ces différents schémas à l'aide du langage de
programmation C++.
Le modèle
d'angiogenèse tumorale développé au cours de mon Doctorat a ainsi permis de
reproduire de façon qualitativement satisfaisante les interactions entre les phénomènes
d'angiogenèse et de croissance tumorale (cf Figure 1).
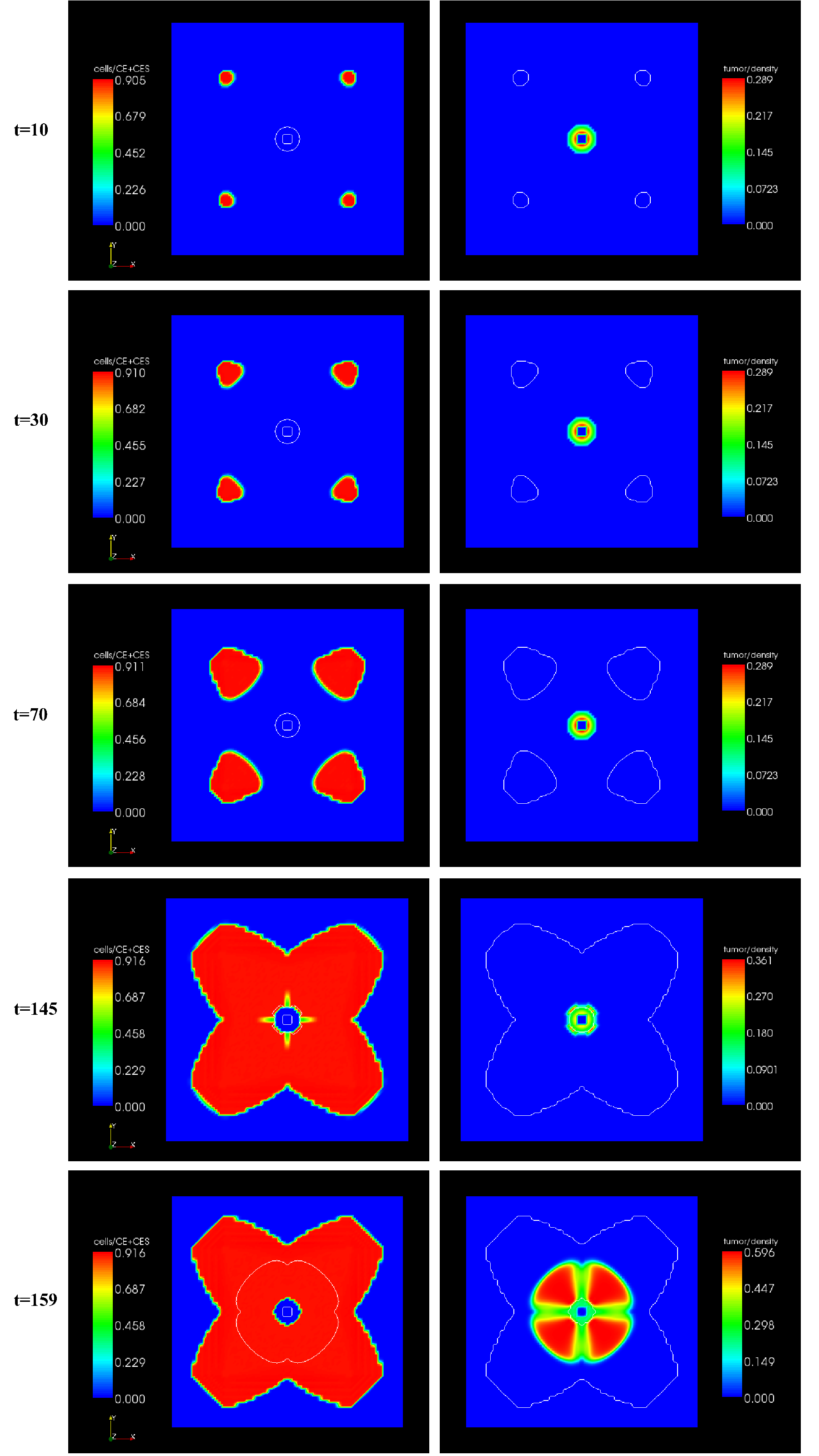
Figure 1 :
De haut en bas :
évolution spatio-temporelle des densités de cellules endothéliales (stables et
instables) et tumorales.
Initialement, une
tumeur circulaire est située au centre du domaine, et supposée entourée de
quatre vaisseaux sanguins préexistants.
Les images de
gauche montrent l'évolution de la densité de cellules endothéliales proliférant
et migrant depuis les vaisseaux préexistants vers la tumeur, sous l'action chemoattractante
du VEGF. Le contour de la tumeur est représenté par un trait fin.
Les images de
droite montrent l'évolution de la densité de cellules tumorales (proliférantes
et quiescentes). Le contour de la distribution de cellules endothéliales est
représenté par un trait fin. Dès que la densité vasculaire est suffisamment
élevée au voisinage de la tumeur, les cellules tumorales périphériques
disposent de l'oxygène nécessaire à leur prolifération.
Ce modèle a également
permis de simuler l'action de différents modes de traitements anti-angiogéniques,
d'analyser leurs effets sur le développement du réseau vasculaire et donc
sur la croissance tumorale, ainsi que leurs modalités d'administration.
J'ai, par exemple, simulé l'action d'une thérapie génique virale basée sur l'injection
intra-tumorale de virus codant pour le gène de l'endostatine. Cette thérapie
consiste à augmenter la production endogène de l'endostatine, substance,
antagoniste du VEGF, sécrétée par les cellules tumorales, et donc à inhiber la
liaison du VEGF aux récepteurs des cellules endothéliales instables. Cette
inhibition engendre directement l'inactivation (non prolifération, non
migration), voire la mort, des cellules endothéliales concernées. Les
simulations ont permis de mettre en évidence l'existence d'une quantité
d'endostatine "critique" en-dessous de laquelle apparaît un effet rebond
: à taux de surproduction (i.e. dose de traitement) constant, une augmentation
de la durée de la surproduction (i.e. de la durée du traitement) induit une
reprise plus rapide de la croissance tumorale après l'arrêt du traitement. Cet
effet rebond s'explique par l'accumulation de molécules de VEGF actif dans le
milieu environnant pendant la durée du traitement, une partie des récepteurs
étant occupée par les molécules d'endostatine. A la fin du traitement, lorsque
les molécules d'endostatine surproduite disparaissent, les cellules
endothéliales instables sont donc sur-stimulées par le VEGF actif, d'où une
reprise plus rapide de l'angiogenèse. Mon modèle a ainsi permis de démontrer
que, dans le cas d'un tel traitement, une augmentation de la durée du
traitement peut être néfaste pour le patient.
Ces résultats in silico illustrent les difficultés
sous-jacentes à l'optimisation de traitements anti-angiogéniques dans la
pratique clinique.
Ces résultats ont
fait l'objet de publications dans les revues Bulletin du Cancer [8] et Journal
of Theoretical Biology [9].
Dans un futur plus
ou moins proche, plusieurs extensions pourraient être apportées à mon modèle
afin de permettre une étude plus précise des mécanismes impliqués dans
l'angiogenèse. Je prévois ainsi de prendre en compte, de façon plus
mécanistique, les interactions biomécaniques (adhésion cellule-cellule, stress,
...) entre le réseau vasculaire, la tumeur et leur environnement. Ces
interactions affectent le développement du réseau vasculaire ainsi que la
croissance tumorale. J'envisage également d'étudier l'action conjuguée d'un
traitement anti-angiogénique et d'un traitement cytotoxique.
Références
[7] D. Bresch, T. Colin, E. Grenier, B. Ribba, and O.
Saut. Computational modeling of solid tumor growth : the avascular stage. SIAM
J Sci Comput, 32 (4): 2321-2344, 2010.
[8] F. Billy, O. Saut, H.
Morre-Trouilhet, T. Colin, D. Bresch, B. Ribba, E. Grenier, JP. Flandrois.
Modèle mathématique multi-échelle de l'angiogenèse tumorale et application à
l'analyse de l'efficacité de traitements anti-angiogéniques. Bull Cancer, 95(NS): 65, 2008
[9] F. Billy, B. Ribba, O. Saut, H.
Morre-Trouilhet, T. Colin, D. Bresch, J.P. Boissel, E. Grenier, and J.P.
Flandrois. A pharmacologically based
multiscale mathematical model of angiogenesis and its use in investigating the efficacy of a new cancer
treatment strategy. J Theor Biol,
260(4) : 545-562, Oct 2009.
Retour à la page d'accueil