




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: Index
Sup.: Le préprocesseur EMC²
Préc.: 1.5.7 Limitations et Bogues
Index
Table des matières
On a utilisé un système de listes à deux éléments que l'on appellera le CAR et le CDR.
L'adresse vide est NIL=0 (parameter).
Dans les schémas suivants le CAR sera toujours à gauche et le CDR à droite.
Les atomes libres sont dans une liste d'atomes libres, la tête de cette liste est FREE.
Les atomes libres sont chaînés par leur CDR.
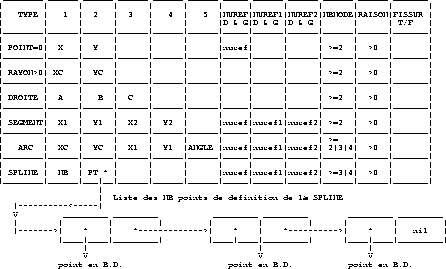
Figure 1.40: Description de la B.D. pour l'application CONSTRUCTION
La figure 1.40 décrit la B.D. pour l'application
CONSTRUCTION
avec,
- TYPE
- le type de l'élément de B.D.
- POINT = 0. POINT X,Y.
- RAYON > 0. CERCLE de centre XC,YC et de rayon RAYON.
- DROITE = -1. DROITE d'équation A*x + B*y + C =0
Avec A*A + B*B = 1
- SEGMENT = -3. SEGMENT allant du point X1,Y1 au point X2,Y2.
- ARC = -2. ARC de centre XC,YC passant par le
point X1,Y1
et faisant un angle ANGLE à partir de ce point.
- SPLINE = -4. SPLINE.
- VIDE = -1000. élément vide.
et pour SPLINE,
- NB est le nombre de points de définition.
- PT est le pointeur sur la liste des POINTS de définition
de la SPLINE.
- NUREF est le numéro de référence de l'élément
(ARC ou SEGMENT). Par défaut NUREF=0.
- NUREF1 est le numéro de référence de l'extrémité 1 de
l'élément (ARC ou SEGMENT). Par défaut NUREF1=0.
- NUREF2 est le numéro de référence de l'extremite 2 de
l'élément (ARC ou SEGMENT). Par défaut NUREF2=0.
- NBNODE est le nombre de points intermédiaires de l'élément
(extrémites comprises). Par défaut NBNODE=2.
- RAISON est la raison de la progression géométrique répartissant
les NBNODE-2 points
de l'extrémité 1 à l'extrémité 2. Par défaut RAISON=1.
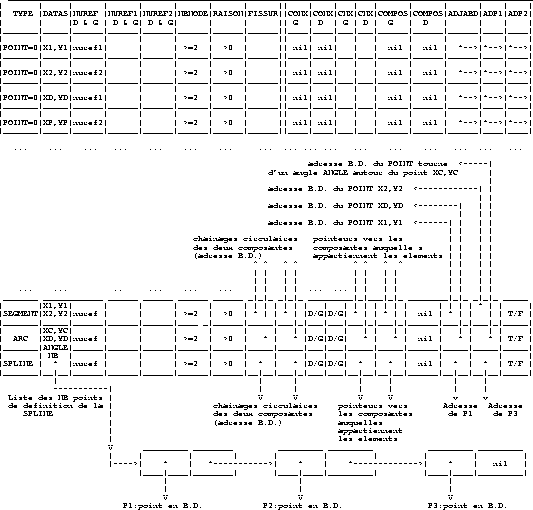
Figure 1.41: Description de la B.D. pour l'application PREP MESH
La figure 1.41 décrit la B.D. pour l'application PREP MESH
où
- TYPE
- est le type de l'élément de B.D.
- POINT = 0. POINT X,Y.
- SEGMENT = -3. SEGMENT allant du point X1,Y1 au point X2,Y2.
- ARC = -2. ARC de centre XC,YC passant par le point XD,YD
et faisant un angle ANGLE à partir de ce point.
- SPLINE = -4. SPLINE.
- VIDE = -1000. élément vide.
- NUREF
- est le numéro de référence de l'élément (ARC ou SEGMENT).
- ADP1
- pointeur dans la B.D. sur le POINT extrémite 1 de l'élément
(Si l'élément n'est pas fissuré, on a dans le NUREF de ce POINT
le numéro de référence de l'extrémité 1 de l'élément).
- ADP2
- pointeur dans la B.D. sur le POINT extrémite 2 de l'élément
ou le dernier POINT de la SPLINE.
(Si l'élément n'est pas fissure,
on a dans le NUREF de ce POINT le numéro de référence de l'extrémité
2 de l'élément).
- NBNODE
- est le nombre de points intermédiaires de l'élément (extrémités comprises).
- RAISON
- est la raison de la progression géométrique répartissant
les NBNODE-2 points de l'extrémité 1 à l'extrémité 2.
- CONX(2)
- pointeurs dans la B.D. Il permet le chaînage circulaire
des éléments d'une même composante connexe.
Pour un même élément, il y a deux et seulement
deux composantes connexes qui contiennent cet élément :
la composante qui est à gauche et celle qui est à droite
(La droite et la gauche sont des notions
relatives au sens de parcourt de l'élément).
Il y a donc deux chaînages symbolisés par : CONXG et CONXD.
- CNX(2)
- indique le CONX à utiliser pour l'élément suivant (CONXG ou CONXD)
selon que CNX vaut GAUCHE/DROIT (GAUCHE=1, DROIT=2)(parameter).
- COMPOS(2)
- pointeurs inverses vers les deux composantes auxquelles appartient l'élément.
CNXG est relatif à CONXG et à COMPOSG ( Ils n'existent que pour les ARCS et les SEGMENTS).
CNXD est relatif à CONXD et à COMPOSD ( Ils n'existent que pour les ARCS et les SEGMENTS).
- ADJABD
- Tête de liste des éléments passant par le point (Il n'existe que pour les POINTS).
(Voir description de cette liste plus loin).
La tête de la liste des éléments passant par un point est
ADJABD.
La figure 1.42 décrit la liste des éléments
passant par le point i.
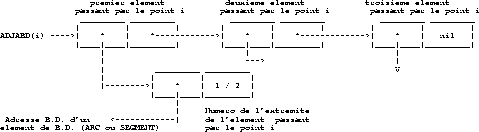
Figure: Description de la liste des éléments passant par le point i
La tête de la liste des composantes est COMP.
La figure 1.43 décrit la liste des composantes.
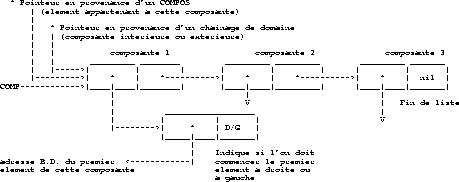
Figure 1.43: Description de la liste des composantes
La tête de la liste des domaines est SDOMN.
La figure 1.44 décrit la liste des domaines
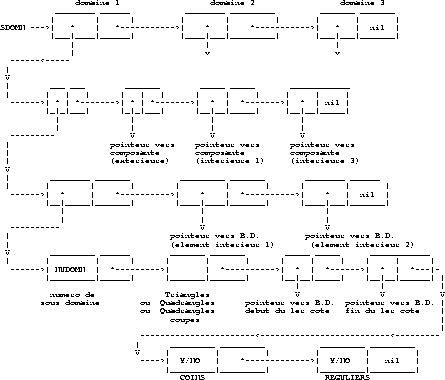
Figure 1.44: Description de la liste des domaines
La base de données est la même que dans l'application PREP_MESH,
et la structure de donnée SD_MESH est formée comme suit:
- nbs
- est le numéro du dernier sommet
- nbt
- est le numéro du dernier triangle
- nba
- est le nombre d'arêtes qui sont sur des courbes (segment, arc, spline)
que l'on appellera arêtes-frontières
- nbsd
- est le nombre de sous-domaines
- nbsrft
- est le nombre de sommets référencés par les éléments
- nbtria
- est le nombre de triangles
- nbquad
- est le nombre de quadrangles
- nbtrou
- est le nombre de trous dans le maillage
- freetr
- est la tête de la liste des triangles détruits
- finbd3
- est le numéro du dernier élément de BD de PREP_MESH
- Les Sommets
- sont définis avec les 4 tableaux en parallèle suivants:
- cr(1:2,nbs)
- est le tableau des coordonnées des sommets.
- nsorig(1:nbs)
- est le tableau donnant le numéro du sommet
d'origine pour les sommets qui sont sur une fissure
(les coordonnées réelles du sommet i sont cr(1:2,nsorig(i)), cr(1:2,i) sont des coordonnées ne servant qu'à la visualisation de la fissure.
Remarque: si le sommet i n'est pas sur une fissure, on a nsorig(i) = i.
- abcurv(1:nbs)
- est :
- 0 si le sommet n'est pas sur une courbe (segment, arc, spline),
(le sommet est interne à un sous-domaine),
- abscisse du point sur la courbe si ce sommet n'est pas une extrémité de la courbe,
0 pour les extrémités de courbe. Remarque: les courbes sont toujours paramétrées de 0 à 1.
- refs(1:nbs)
- est le tableau donnant: le numéro dans BD de l'élément (point, segment, arc, spline)
supportant le sommet si il existe, sinon 0.
Remarque: si le sommet est une extrémité de courbe alors l'élément choisi
sera le point extrémité de courbe (c.f. ADP1 et ADP2 (Annexe 1.5.8))
- Les éléments finis
- sont des triangles ou des quadrangles qui sont représentés
de manière interne uniquement avec triangles auxquels on a ajouté
la notion d'arête visible ou non afin de tracer les quadrangles. Les tableaux
définissant les triangles sont:
- nsea(1:6,nbt)
- définit pour chaque triangle les sommets et les arêtes ou les triangles adjacents
si nsea(1,ie)< 1 alors le triangle ie n'existe pas
et reft(ie) donne le triangle détruit suivant,
sinon le triangle ie existe et on a :
- nsea(1:3,ie) donne pour chaque triangle les trois numéros de sommets
tournant dans le sens trigonométrique.
-
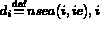 =
4,5,6, les 3 arêtes
=
4,5,6, les 3 arêtes  du triangle numérotées de 4 à 6 ont pour sommets
nsorig(nsea(i-3,ie)) et (nsorig(nsea(mod(i,3)+1,ie)).
du triangle numérotées de 4 à 6 ont pour sommets
nsorig(nsea(i-3,ie)) et (nsorig(nsea(mod(i,3)+1,ie)).
- si
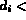 0 alors l'arête est frontière,
et est définie dans aretdb, et a pour numéro
0 alors l'arête est frontière,
et est définie dans aretdb, et a pour numéro  ;
;
- sinon l'arête est interne et
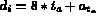 où
où 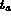 est le numéro du triangle adjacent à l'arête
et
est le numéro du triangle adjacent à l'arête
et 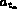 est le numéro de l'arête dans
est le numéro de l'arête dans 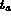 .
.
- anovue(1:nbt)
- donne pour chaque triangle la
visibilité de ses 3 arêtes, si anovue(i) est égal à :
- 0
- toutes les arêtes du triangle i sont vues,
- 1
- seule l'arête 4 du triangle i n'est pas vue,
- 2
- seule l'arête 5 du triangle i n'est pas vue,
- 3
- seule l'arête 6 du triangle i n'est pas vue,
- reft(1:nbt)
- est:
- soit le tableau des numéros du sous-domaine contenant le triangle;
- soit le tableau de chaînage des triangles d'un sous-domaine,
(reft(ie) donne le triangle suivant du sous-domaine,
si reft(ie) <> finsd =
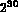 ,voir aussi le tableau tetdt
pour les têtes de liste des sous-domaines).
,voir aussi le tableau tetdt
pour les têtes de liste des sous-domaines).
- Les arêtes-frontières
- du maillages sont définies comme suit:
- aretbd(1:2,nba)
- donne pour chaque arête ses 2 numéro de sommets;
- areadj(gauche:droite,nba)
- :
 = gauche,droite
même définition que pour nsea;
= gauche,droite
même définition que pour nsea;
- refa(nba)
- donne pour chaque arête l'adresse dans la bd du support
de celle-ci (le support existe toujours par définition).
- Les sous-domaines
- sont définis avec les tableaux suivants:
- refsd(nbsd)
- donne les numéros de référence
des sous-domaines, si refsd(i) = videsd =
 alors le
sous-domaine n'existe pas.
alors le
sous-domaine n'existe pas.
- trfsd(3,3,i)
-
donne la transformation appliquée au sous-domaine ptorsd(i)
pour obtenir ce sous-domaine i (
 )
)
- strfsd(i)
- donne le signe de la transformation
(exemple: -1 pour une symétrie par rapport à une droite)
- ptorsd(i)
- donne le numéro sur le sous-domaine origine
(si ptorsd(i)=i alors le sous-domaine i n'est pas transformé (sous-domaine original))
- tetsd(nbsd)
- est un tableau donnant par sous-domaine le premier triangle de la liste
des triangles de ce sous-domaine (c.f reft)
Le maillage n'est formé que de triangles et peux être défini
avec les 2 entiers et les 4 tableaux suivants :
- nbt
- est le nombre de triangles
- nbs
- est le nombre de sommets
- nu(1:3,1:nbt)
- est un tableau d'entiers donnant pour chaque triangle
les trois numéros de sommets
dans le sens trigonométrique.
- c(1:2,nbs)
- est un tableau de réels donnant les 2 coordonnées pour chaque sommet.
- refs(nbs)
- est un tableau d'entier donnant les numéros de référence des sommets.
- reft(nbs)
- est un tableau d'entiers donnant les numéros de référence des triangles.
Remarque: les sommets non référencés par des triangles seront éliminés,
la numérotation des sommets dans ce cas sera compressée.
La lecture d'un fichier xxx.am est faite comme suit :
open(1,file='xxx.am',form='unformatted',status='old')
read (1) nbs,nbt
read (1)
+ ((nu(i,j),i=1,3),j=1,nbt)
+ ,((c(i,j),i=1,2),j=1,nbs)
+ ,( reft(i),i=1,nbt)
+ ,( refs(i),i=1,nbs)
close(1)
La lecture d'un fichier xxx.am_fmt est faite comme suit :
open(1,file='xxx.am_fmt',form='formatted',status='old')
read (1,*) nbs,nbt
read (1,*) ((nu(i,j),i=1,3),j=1,nbt)
read (1,*) ((c(i,j),i=1,2),j=1,nbs)
read (1,*) ( reft(i),i=1,nbt)
read (1,*) ( refs(i),i=1,nbs)
close(1)
La lecture d'un fichier xxx.amdba est faite comme suit :
open(1,file='xxx.am_fmt',form='formatted',status='old')
read (1,*) nbs,nbt
read (1,*) (k,(c(i,k),i=1,2),refs(k),j=1,nbs)
read (1,*) (k,(nu(i,k),i=1,3),reft(k),j=1,nbt)
close(1)






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: Index
Sup.: Le préprocesseur EMC²
Préc.: 1.5.7 Limitations et Bogues
Index
Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()





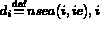 =
4,5,6, les 3 arêtes
=
4,5,6, les 3 arêtes 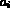 du triangle numérotées de 4 à 6 ont pour sommets
nsorig(nsea(i-3,ie)) et (nsorig(nsea(mod(i,3)+1,ie)).
du triangle numérotées de 4 à 6 ont pour sommets
nsorig(nsea(i-3,ie)) et (nsorig(nsea(mod(i,3)+1,ie)).
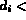 0 alors l'arête est frontière,
et est définie dans aretdb, et a pour numéro
0 alors l'arête est frontière,
et est définie dans aretdb, et a pour numéro  ;
;
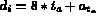 où
où 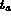 est le numéro du triangle adjacent à l'arête
et
est le numéro du triangle adjacent à l'arête
et 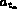 est le numéro de l'arête dans
est le numéro de l'arête dans 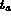 .
.
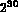 ,voir aussi le tableau tetdt
pour les têtes de liste des sous-domaines).
,voir aussi le tableau tetdt
pour les têtes de liste des sous-domaines).
 = gauche,droite
même définition que pour nsea;
= gauche,droite
même définition que pour nsea;
 alors le
sous-domaine n'existe pas.
alors le
sous-domaine n'existe pas.
 )
)