Suiv.: 1.5.2 Les menus globaux Sup.: Le préprocesseur EMC² Préc.: Le préprocesseur EMC² Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 1.5.2 Les menus globaux
Sup.: Le préprocesseur EMC²
Préc.: Le préprocesseur EMC²
Index
Table des matières
Le logiciel est divisé en trois applications principales (exclusives):
Dans chacune de ces applications on accède aussi aux menus suivants
Chaque application (principale) possède un menu qui lui est propre. Toutes les applications sont dirigées par des grammaires LL1.

Figure: Représentation de l'écran
L'écran (figure 1.9) est découpé en 9 zônes: 5 sont des menus ((1), (2), (4), (7), (6)), 3 sont des zônes d'affichage ((8), (9), (5)) , la zône centrale est graphique.
Les menus GENERAL(ITES), CALCULETTE, GESTION DE L'ECRAN sont fixes et indépendants des applications. Les menus APPLICATION et DESIGNATION sont évidemment dépendants de l'application en cours.
Le logiciel est interactif, toutes les entrées se font à l'aide de la souris et du clavier. La souris permet de désigner les ITEM (cases) des menus ainsi que les éléments graphiques (après sélection dans le menu DESIGNATION). Le clavier permet d'entrer du texte (par exemple le nom d'un fichier) ainsi que des raccourcis, (les ITEM de certains menus ont été mis en équivalence avec des touches du clavier).
Cette application permet de définir les contours géométriques du domaine à l'aide de points, segments, arcs de cercle, et de splines. On a de plus introduit deux autres entités de construction qui sont utiles dans certains cas: les droites et les cercles. Ces deux dernières entités ne servent d'ailleurs que dans cette application.
On peut construire toutes les entités, excepté les splines, à l'aide des théorèmes de géométrie élémentaire; quand les solutions sont multiples, les ambiguïtés sont levées en utilisant l'heuristique suivante: les points de désignation sont proches des points de tangence des éléments (point, droite, cercle, arc, segment).
Une spline est définie comme une courbe  passant par une
liste de points. Elle sera fermée si le premier et le dernier
point sont confondus.
passant par une
liste de points. Elle sera fermée si le premier et le dernier
point sont confondus.
On peut dupliquer toutes ces entités à l'aide des transformations affines suivantes: symétrie, rotation, homothétie, translation.
De plus on peut :
A ce niveau les composantes connexes des bords des sous-domaines
de  sont connues. On appellera ces composantes connexes, des
composantes.
sont connues. On appellera ces composantes connexes, des
composantes.
Cette application permet de définir la discrétisation sur les entités définissant le bord du domaine et des sous-domaines (frontière de matériaux), ainsi que des numéros de références sur les sous-domaines, sur les lignes, sur les points; en vue d'entrer des données physiques différentes (exemple: plusieurs conditions aux limites, plusieurs matériaux).
Elle permet aussi de créer un fichier de données en vue d'interfacer le mailleur de MODULEF: APNOXX, en définissant les sous-domaines comme une liste de composantes où la 1ère est la composante extérieure (les autres composantes étant les composantes des trous), plus des lignes internes, et des points internes à forcer.
Au moment de la commutation on peut modifier la valeur par défaut de certains paramètres du mailleur. Le programme construit un maillage triangulaire ou quadrangulaire réglé des sous-domaines définis à l'étape précédente, ou bien de tous les sous-domaines si aucun n'a été défini.
A ce niveau on peut éditer le maillage:
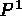 ou
ou 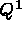 .
.
Pour changer les habitudes nous allons mailler un cercle unité plutôt
qu'un carré. Il faut donc construire le cercle (un arc de 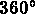 ) ,
puis définir la discrétisation sur l'arc, puis construire le maillage.
Ces 3 phases correspondent respectivement aux trois applications CONSTRUCTION,
PREP_MESH, EDIT_MESH.
) ,
puis définir la discrétisation sur l'arc, puis construire le maillage.
Ces 3 phases correspondent respectivement aux trois applications CONSTRUCTION,
PREP_MESH, EDIT_MESH.
La liste des actions :
 s'affiche.
Remarque: bien que la variable d'état "angle" soit égale à 0,
l'angle de l'arc est en fait égale à 360
s'affiche.
Remarque: bien que la variable d'état "angle" soit égale à 0,
l'angle de l'arc est en fait égale à 360 (0
(0  360 mod 360).
360 mod 360).
Pour définir le nombre de point sur l'arc il suffit de:
Construction d'un maillage entre les 8 cercles tangents aux 3 cercles en pointillés (c.f. figure 1.13). On a coupé les arcs au voisinage des points de ''presque tangence'' en vue de raffiner le maillage. On montre les différentes étapes (figures 1.13,1.14 et 1.15), et des agrandissements du maillage figures 1.16 et 1.17. La figure 1.17 étant un très fort zoom (environ 360 fois) autour d'un point de presque tangence.
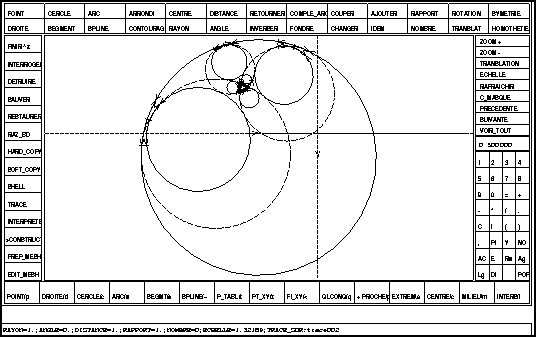
Figure: La géométrie du domaine
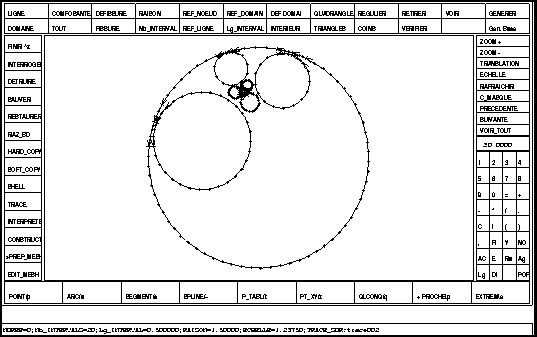
Figure: La discrétisation des contours

Figure 1.15: Visualisation du maillage total
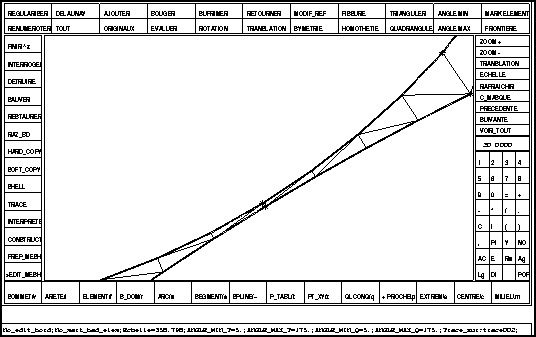
Figure 1.17: Zoom autour l'un des points de presque tangence