Suiv.: L'application PREP_MESH Sup.: Le préprocesseur EMC² Préc.: 1.5.2 Les menus globaux Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: L'application PREP_MESH
Sup.: Le préprocesseur EMC²
Préc.: 1.5.2 Les menus globaux
Index
Table des matières
Cette application est dirigée par le menu de l'application (figure 1.24) en haut de l'écran et le menu de désignation (figure 1.18) en bas de l'écran. Elle permet de construire des objets 2D définis à partir des points, segments, arcs et splines; les cerles et les droites ne servant que d'artifices de construction. Elle permet de construire et manipuler ces objets:

Figure 1.24: Le menu de l'application CONSTRUCTION
Nous rappelons que grâce aux menus de désignation on peut désigner des points, droites, cercles, arcs, segments, splines, coordonnées (points immédiats, extrémités, etc...). Donc nous noterons par <POINT> , <DROITE> , <CERCLE> , <SEGMENT> , <ARC> , <SPLINE> , <COORD> le fait de désigner un de ces éléments ou une partie de ceux-ci, de plus on crée une <VALEUR> en utilisant la calculette ou ses raccourcis (voir les sections 1.5.2,1.5.2 pour plus de détails).
Nous utiliserons, dans la méta syntaxe de description du langage de construction, les symboles suivants:
Nous appellerons xxx une suite d'actions qui seront définies par <xxx> = ... . ;
Exemple : L'expression : <xxx> = ( A | ") *(B|C) E ; nous permet d'entrer des suites de lettres (chaîne) commençant ou non par A formé de B ou de C en suite et ce terminant par E.
Exemple de chaînes admissibles :
ABBCCCCE E AE CBCBCBCBCBCBCBE ABBBBBBBE BE ABE BCBCBCBCBCBCBCE BBBBBBBBBE CE ACE CCCCCCCCCCCCCCE
Nous appellerons
ou encore, dans la méta syntaxe :
<point_coor> = <POINT> | <COORD>;
<contrainte> = <point_coor> | <DROIT> | <CERCLE> | <ARC>
| <SEGMENT>;
<element> = <contrainte> | <SPLINE>;
Dans la définition de contrainte, l'ARC est assimilé au cercle qui le supporte, de même que
SEGMENT est assimilé à la droite qui le supporte.
Remarque:
En base de données les éléments sont décrits par:
| POINT | (a,b) avec: x=a; y=b |
| DROITE | (a,b,c) tels que ax+by+c=0 |
| CERCLE | centre(a,b) et rayon r |
| SEGMENT | (P1,P2) avec P1=(x1,y1) et P2=(x2,y2) |
| ARC | centre en P1 passant par P2 et d'angle 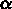 , , |
| avec P1=(x1,y1) et P2=(x2,y2) | |
| SPLINE | (nombre de points, tête de la liste des points) |
Au niveau de l'application CONSTRUCTION tous les menus autres que le menu de CONSTRUCTION sont filtrés par les applications DESIGNATION, CALCULETTE, GENERALITE, GESTION DE L'ECRAN GRAPHIQUE. Donc le fait de cliquer dans ces menus n'a aucune action directe sur l'application (excepté le changement de type de désignation ou l'entrée d'une valeur). Les cases du menu de l'application et les désignations gouvernent l'application CONSTRUCTION. Par la même nous noterons XXXX : le fait de cliquer dans la case XXXX du menu de l'application courante (en haut). Il n'y aura aucune confusion avec des cases de même nom d'un autre menu.
exemple:
L' état du système est un ensemble de variables qui sont utilisées par l'application, ces variables globales à l'application sont :
Nous appellerons <modif etat> une modification de l'état du système , c'est à dire une modification de la valeur affectée à l'une des variables
<modif etat> = *( <distance> | <rayon> | <angle> | <rapport> | <nombre> )
POINT
*( <COORD>
| <POINT> ( <CERCLE> | <DROITE>
| <ARC> | <SEGMENT> | <SPLINE> )
| <DROITE> <element>
| <CERCLE> <element>
| <SPLINE> <element>
);
Exemple de construction de points
On commence par cliquer dans la case POINT du menu construction pour se mettre en mode de construction de points puis
DROITE *( <contrainte> <contrainte>
| IDEM *<SEGMENT>
);
Si on a comme contraintes (indépendamment de tout ordre) :
CERCLE
*( <rayon> *( CENTRE <point_coor> | <contrainte> <contrainte>)
| <contrainte> ( <rayon> <contrainte>
| <contrainte> ( <rayon> | <contrainte> ))
| CENTRE <point> *(<rayon> | <contrainte>)
| IDEM *<ARC>
);
Explication des différents cas (indépendamment de l'ordre)
ARC *( CENTRE <point> *( <angle> <contrainte>
| <rayon>
| <contrainte> (<angle> | <contrainte>))
| <rayon> *( CENTRE <point>
| <contrainte> <contrainte> )
| <contrainte> ( <rayon> <contrainte>
| <contrainte> (<rayon> | <contrainte>))
| IDEM *<CERCLE>
);
Explication des différents cas (indépendamment de l'ordre).
Pour la construction des ARCS, on crée d'abord le cercle ayant les mêmes contrainte et on prend
un arc sur ce cercle.
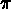
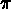 sur chaque cercle désigné.
sur chaque cercle désigné.
SEGMENT *( <contrainte> <contrainte> );Explication des différents cas (indépendamment de l'ordre).
Pour la construction des SEGMENTS, on commence par créer la DROITE ayant les mêmes contraintes puis on prend un segment de cette droite reliant les deux points de tangence aux deux containtes si ils existent, sinon on ce sert de la variable d'état
Par exemple :
SPLINE <point> *<point>;Construit la spline (cubique par morceaux) passant par les points. On peut faire une spline fermée en définissant le dernier point identique au premier (en le désignant).
ROTATION , TRANSLAT , HOMOTHETIE , SYMETRIE définissent des transformations que l'on va appliquer sur les éléments désignés.
ROTATION <modif etat> ( CENTRE | " ) <point_coor> <modif etat> *<element> TRANSLAT <point_coor> <point_coor> *<element> HOMOTHETIE <modif etat> CENTRE (<point_coor> | " ) <modif etat> *<element> SYMETRIE (<point_coor> | <DROITE>| <SEGMENT>) *<element>
 1, on déplace elements sinon on crée
1, on déplace elements sinon on crée
 1, on déplace
1, on déplace
 1, on déplace elements sinon on crée %NOMBRE-1 nouvelles occurences de elements.
(Donc le nombre d'occurences de elements sur l'écran après la transformation est %NOMBRE).
1, on déplace elements sinon on crée %NOMBRE-1 nouvelles occurences de elements.
(Donc le nombre d'occurences de elements sur l'écran après la transformation est %NOMBRE).
Cette commande permet de faire des arrondis entre SEGMENTS et ARCS.
ARRONDI *( <contrainte> <contrainte> )On crée un arrondi de rayon %RAYON entre les deux contrainte, l'arrondi tourne toujours dans le sens positif. L'arrondi est un arc dont le cercle qui le supporte est tangent aux deux contrainte, l'arc va du premier point de tangence au deuxième point de tangence en tournant dans le sens positif. Si une contrainte est un ARC ou un SEGMENT, on modifie cette contrainte de façon à ce que cet élément se termine au point de tangence avec l'arrondi.
CONTOURAGE (<DROITE> | <CERCLE>) (<DROITE> | <CERCLE>)
(<DROITE> | <CERCLE>) (COMPLE_ARC | ")
*( (<DROITE> | <CERCLE>) (COMPLE_ARC | ") )
Permet de définir un contour formé de SEGMENTS et d'ARCS s'appuyant sur un ensemble de droites et de cercles.
Le programme fonctionne en calculant l'intersection de la contrainte i avec la contrainte i+1 ce qui donne le point I
puis la contrainte i+1 avec la i+2 ce qui donne le point I+1, I et I+1 forment un nouveau morceau du contour
et ainsi de suite.
Par exemple avec des droites (figure 1.25) :
Supposons que nous avons les 5 droites 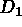
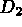

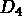
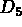 s'intersectant
en
s'intersectant
en 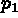


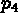
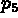 et que nous voulons définir le
contour formé des segments
et que nous voulons définir le
contour formé des segments 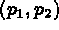 ,
, 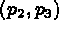 ,
, 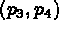 ,
, 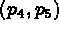 ,
, 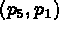 .
On désigne par +i le ième point de désignation.
.
On désigne par +i le ième point de désignation.
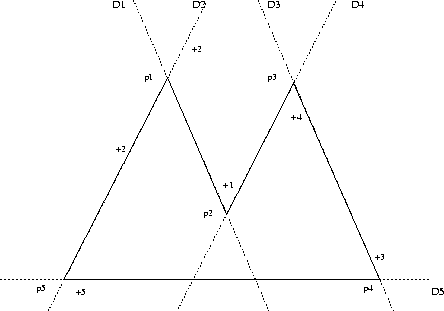
Figure 1.25: Exemple de contourage
On désigne 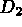 en +2 puis
en +2 puis 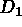 en +1 ce qui défini
en +1 ce qui défini 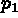
Puis on désigne 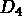 en +4 ce qui définit
en +4 ce qui définit  (ici le programme trace
(ici le programme trace 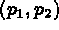
Puis on désigne  en +3 ce qui définit
en +3 ce qui définit  (ici le programme trace
(ici le programme trace 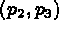
Puis on désigne 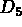 en +5 ce qui définit
en +5 ce qui définit 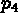 (ici le programme trace
(ici le programme trace 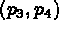
Puis on désigne 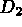 en +2 ce qui définit
en +2 ce qui définit 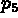 (ici le programme trace
(ici le programme trace 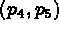
Puis on désigne 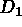 en +1 ce qui définit
en +1 ce qui définit 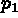 (ici le programme trace
(ici le programme trace 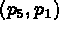
Dans le cas de cercles il faut faire attention car les points de désignation servent à lever les ambiguïtés d'intersections multiples (le point de désignation de la contrainte i sert à lever l'ambiguïté de désignation entre les contraintes i et i+1).
RETOURNE *( <ARC> | <SEGMENT> )
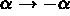
 (P1,2*P1-P2) (Symétrie / P1)
(P1,2*P1-P2) (Symétrie / P1)
COMPLE_ARC *ARCChange un ARC en son complément si (
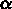 <0) alors
<0) alors 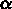 =
= 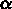 +2
+2
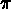 sinon
sinon 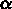 =
= 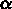 - 2
- 2 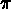
INVERSER *(<ARC> | <SEGMENT> | <SPLINE>)
Inverse un ARC, SEGMENT ou une SPLINE


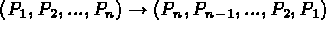
COUPER * ( <point_coor> *(<ARC> | <SEGMENT> | <SPLINE>)
| (<DROITE> | <CERCLE> | <ARC> | <SEGMENT> | <SPLINE>)
(<DROITE> | <CERCLE> | <ARC> | <SEGMENT> | <SPLINE>)
)
Si on désigne point en premier on
coupe en deux un ARC ou un SEGMENT ou une SPLINE
par la projection de point sur l'élément.
CHANGER *( ANGLE <ARC> (<VALEUR> | IDEM)
| RAYON <CERCLE> (<VALEUR> | IDEM)
| <POINT> <point_coor>)
Permet donc de changer :
AJOUTER *( POINT *( <ARC> | <SEGMENT> | <SPLINE> | <POINT> <POINT> )
| SEGMENT *( <SEGMENT> <SEGMENT> )
| SPLINE *( <SPLINE> ( <SPLINE> | *<POINT> ) )
| ARC *( <ARC> <ARC> )
FONDRE *( <segment> <segment> | <arc> <arc> | <spline> <spline> )
Permet de fondre 2 SEGMENTS ou 2 ARCS ou 2 SPLINES ayant une extrémité commune en un seul élément de même type. L'élément résultant est dans le sens du premier désigné. Pour que cette instruction puisse s'effectuer, il faut: