Suiv.: Méthode d'extrusion (topologie cylindrique) Sup.: Méthode de blocs Préc.: Le préprocesseur COLIXX Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Méthode d'extrusion (topologie cylindrique)
Sup.: Méthode de blocs
Préc.: Le préprocesseur COLIXX
Index
Table des matières
A titre d'exemples nous donnons:
Suit le programme d'appel de COLIB2 dans le cas d'un élément pentaédrique.
La figure 3.3 montre le maillage obtenu pour 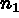 = 4 et
= 4 et
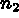 = 5 où
= 5 où 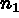 et
et 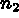 désignent respectivement le nombre de points sur
les arêtes des faces triangulaires et le nombre de tels points sur les autres
arêtes.
désignent respectivement le nombre de points sur
les arêtes des faces triangulaires et le nombre de tels points sur les autres
arêtes.
C +++++++++++++++++++++
C TEST PENTAEDRE COLIB2
c +++++++++++++++++++++
PARAMETER ( LM = 100000 )
COMMON M(LM)
DIMENSION XYZ(3,6),NTNRS(6),NARET(5,9),NSUP(11,1),
+ NTFR(6,2),XYZINT(3,1)
C
DATA XYZ / 0. , 0. , 0. , 3. , 0. , 0. , 0. , 3. , 0. ,
+ 0. , 0. , 4. , 3. , 0. , 4. , 0. , 3. , 4. /
DATA NTNRS / 1 , 2 , 3 , 4 , 5 , 6 /
DATA NARET / 1,2,0,4,1, 2,3,0,4,2, 3,1,0,4,3,
+ 1,4,0,4,4, 2,5,0,4,5, 3,6,0,4,6,
+ 4,5,0,4,7, 5,6,0,4,8, 6,4,0,4,9/
DATA NTFR / 7,3,1,2,3,0, 8,3,4,5,6,0/
DATA NSUP / 6,1,2,3,4,5,6,0,0,6,1/
C
IMPRE = -2
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
NFNOPO = 10
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'pentacol2.nopo','UNKNOWN,UNFORMATTED',2000000)
C
NDIM = 3
NBS = 6
NA = 9
NBGRO = 1
NBFR = 2
print *,' NOMBRE DE POINTS INTERNE A UNE ARETE DE TRIANGLE ? '
CALL LIBENT(NPINT)
DO 1 I=1,9
NARET(4,I) = NPINT
1 CONTINUE
print *,' NOMBRE DE POINTS INTERNE A UNE ARETE DE QUADRANGLE ? '
CALL LIBENT(NPINT)
DO 2 I=4,6
NARET(4,I) = NPINT
2 CONTINUE
C
CALL COLIB2(M,NFNOPO,NINOPO,NDIM,NBS,NA,NBGRO,NBFR,
+ XYZ,NTNRS,NARET,XYZINT,NTFR,NSUP)
STOP
END
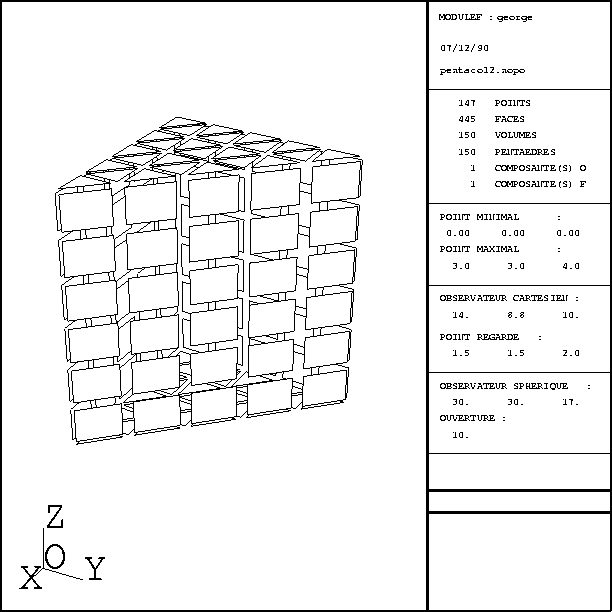
Figure: Maillage d'un pentaèdre via COLIB2
Suit le programme d'appel de COLIBR dans le cas de la construction d'un maillage 2D à partir de 17 blocs de nature triangulaire et quadrangulaire. Le maillage résultat est celui de la figure 3.4.
C ++++++++++++++++++++++++++++++++++++++++++++++
C TEST COLIBR ( COLIB2 AVEC FICHIER DE DONNEES )
C ( UN EXEMPLE EN DIMENSION 2 )
C ++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 300000 )
COMMON M(LM)
C
IMPRE = -2
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
NFNOPO = 10
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'tunnel.nopo','UNKNOWN,UNFORMATTED',2000000)
C
NFDATA = 11
CALL TRUNIT (NFDATA)
CALL OUVRIS(NFDATA,'tunnel.data','UNKNOWN,FORMATTED',2000000)
C
CALL LECTEU(NFDATA)
CALL COLIBR(M,NFNOPO,NINOPO)
STOP
END
Le fichier de données nécessaire est le suivant:
$ NBS NA NBGRO IMPRE NBFR NDIM $
19 35 17 2 0 2
$ NOP NOREF X Y Z ? $
1 1 0.000000E+00 0.000000E+00 0.000000E+00
2 2 0.110000E+02 0.000000E+00 0.000000E+00
3 3 0.110000E+02 0.900000E+01 0.000000E+00
4 4 0.110000E+02 0.180000E+02 0.000000E+00
5 5 0.200000E+01 0.180000E+02 0.000000E+00
6 6 0.000000E+00 0.180000E+02 0.000000E+00
7 7 0.000000E+00 0.400000E+01 0.000000E+00
8 8 0.800000E+01 0.400000E+01 0.000000E+00
9 9 0.800000E+01 0.800000E+01 0.000000E+00
10 10 0.600000E+01 0.110000E+02 0.000000E+00
11 11 0.200000E+01 0.110000E+02 0.000000E+00
12 12 0.000000E+00 0.800000E+01 0.000000E+00
13 13 0.200000E+01 0.600000E+01 0.000000E+00
14 14 0.550000E+01 0.600000E+01 0.000000E+00
15 15 0.550000E+01 0.750000E+01 0.000000E+00
16 16 0.490000E+01 0.900000E+01 0.000000E+00
17 17 0.290000E+01 0.910000E+01 0.000000E+00
18 18 0.200000E+01 0.750000E+01 0.000000E+00
19 19 0.400000E+01 0.750000E+01 0.000000E+00
$ NA IEX1 IEX2 IDEC NP NOREF $
1 1 2 0 5 1
2 2 3 0 5 1
3 3 4 0 5 1
4 4 5 0 5 1
5 5 6 0 5 1
6 6 12 0 4 1
7 12 7 0 5 2
8 7 1 0 4 1
9 7 8 0 5 2
10 8 2 0 4 0
11 8 9 0 5 2
12 9 10 0 5 2
13 9 3 0 4 0
14 10 4 0 4 0
15 10 11 0 5 2
16 12 11 0 5 2
17 11 5 0 4 0
18 13 7 0 5 0
19 14 8 0 5 0
20 15 9 0 5 0
21 16 10 0 5 0
22 17 11 0 5 0
23 18 12 0 5 0
24 13 14 0 5 3
25 14 15 0 5 3
26 15 16 1 5 3
5.45 7.75 0.
5.4 8. 0.
5.3 8.25 0.
5.2 8.50 0.
5.1 8.75 0.
27 16 17 1 5 3
4.5 9.3 0.
4.25 9.45 0.
4.0 9.5 0.
3.5 9.45 0.
3.25 9.3 0.
28 17 18 1 5 3
2.60 8.75 0.
2.40 8.50 0.
2.25 8.25 0.
2.10 8.0 0.
2.05 7.75 0.
29 18 13 0 5 3
30 19 13 0 5 0
31 19 14 0 5 0
32 19 15 0 5 0
33 19 16 0 5 0
34 19 17 0 5 0
35 19 18 0 5 0
$ ELEMENTS GROSSIERS $
$ I NCGE SOMMETS NCGE NDSD $
1 4 1 2 8 7 4 1
2 4 2 3 9 8 4 1
3 4 3 4 10 9 4 1
4 4 10 4 5 11 4 1
5 4 11 5 6 12 4 1
6 4 7 13 18 12 4 2
7 4 7 8 14 13 4 2
8 4 8 14 15 9 4 2
9 4 15 9 10 16 4 2
10 4 16 10 11 17 4 2
11 4 18 17 11 12 4 2
12 3 13 14 19 3 3
13 3 14 15 19 3 3
14 3 15 16 19 3 3
15 3 16 17 19 3 3
16 3 19 18 17 3 3
17 3 13 19 18 3 3

Figure 3.4: Maillage 2D via COLIBR
Suit le programme d'appel de COLIBR dans le cas de la construction d'un maillage 3D à partir de 12 blocs de nature pentaédrique et hexaédrique. Le maillage résultat est celui de la figure 3.5.
C ++++++++++++++++++++++++++++++++++++++++++++++
C TEST COLIBR ( COLIB2 AVEC FICHIER DE DONNEES )
C ( UN EXEMPLE EN DIMENSION 3)
C ++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 300000 )
COMMON M(LM)
C
IMPRE = -2
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
NFNOPO = 10
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'parttun.nopo','UNKNOWN,UNFORMATTED',2000000)
C
NFDATA = 11
CALL TRUNIT (NFDATA)
CALL OUVRIS(NFDATA,'parttun.data','UNKNOWN,FORMATTED',2000000)
C
CALL LECTEU(NFDATA)
CALL COLIBR(M,NFNOPO,NINOPO)
STOP
END
Le fichier de données nécessaire est le suivant:
$ NBS NA NBGRO IMPRE NBFR NDIM $
26 61 12 2 0 3
$ NOP NOREF X Y Z ? $
1 7 0.000000E+00 0.400000E+01 0.000000E+00
2 8 0.800000E+01 0.400000E+01 0.000000E+00
3 9 0.800000E+01 0.800000E+01 0.000000E+00
4 10 0.600000E+01 0.110000E+02 0.000000E+00
5 11 0.200000E+01 0.110000E+02 0.000000E+00
6 12 0.000000E+00 0.800000E+01 0.000000E+00
7 13 0.200000E+01 0.600000E+01 0.000000E+00
8 14 0.550000E+01 0.600000E+01 0.000000E+00
9 15 0.550000E+01 0.750000E+01 0.000000E+00
10 16 0.490000E+01 0.900000E+01 0.000000E+00
11 17 0.290000E+01 0.910000E+01 0.000000E+00
12 18 0.200000E+01 0.750000E+01 0.000000E+00
13 19 0.400000E+01 0.750000E+01 0.000000E+00
14 7 0.000000E+00 0.400000E+01 1.000000E+01
15 8 0.800000E+01 0.400000E+01 1.000000E+01
16 9 0.800000E+01 0.800000E+01 1.000000E+01
17 10 0.600000E+01 0.110000E+02 1.000000E+01
18 11 0.200000E+01 0.110000E+02 1.000000E+01
19 12 0.000000E+00 0.800000E+01 1.000000E+01
20 13 0.200000E+01 0.600000E+01 1.000000E+01
21 14 0.550000E+01 0.600000E+01 1.000000E+01
22 15 0.550000E+01 0.750000E+01 1.000000E+01
23 16 0.490000E+01 0.900000E+01 1.000000E+01
24 17 0.290000E+01 0.910000E+01 1.000000E+01
25 18 0.200000E+01 0.750000E+01 1.000000E+01
26 19 0.400000E+01 0.750000E+01 1.000000E+01
$ NA IEX1 IEX2 IDEC NP NOREF $
1 6 1 0 5 2
2 1 2 0 5 2
3 2 3 0 5 2
4 3 4 0 5 2
5 4 5 0 5 2
6 6 5 0 5 2
7 7 1 0 5 0
8 8 2 0 5 0
9 9 3 0 5 0
10 10 4 0 5 0
11 11 5 0 5 0
12 12 6 0 5 0
13 7 8 0 5 3
14 8 9 0 5 3
15 9 10 1 5 3
5.45 7.75 0.
5.4 8. 0.
5.3 8.25 0.
5.2 8.50 0.
5.1 8.75 0.
16 10 11 1 5 3
4.5 9.3 0.
4.25 9.45 0.
4.0 9.5 0.
3.5 9.45 0.
3.25 9.3 0.
17 11 12 1 5 3
2.60 8.75 0.
2.40 8.50 0.
2.25 8.25 0.
2.10 8.0 0.
2.05 7.75 0.
18 12 7 0 5 3
19 13 7 0 5 0
20 13 8 0 5 0
21 13 9 0 5 0
22 13 10 0 5 0
23 13 11 0 5 0
24 13 12 0 5 0
25 19 14 0 5 2
26 14 15 0 5 2
27 15 16 0 5 2
28 16 17 0 5 2
29 17 18 0 5 2
30 19 18 0 5 2
31 20 14 0 5 0
32 21 15 0 5 0
33 22 16 0 5 0
34 23 17 0 5 0
35 24 18 0 5 0
36 25 19 0 5 0
37 20 21 0 5 3
38 21 22 0 5 3
39 22 23 1 5 3
5.45 7.75 10.
5.4 8. 10.
5.3 8.25 10.
5.2 8.50 10.
5.1 8.75 10.
40 23 24 1 5 3
4.5 9.3 10.
4.25 9.45 10.
4.0 9.5 10.
3.5 9.45 10.
3.25 9.3 10.
41 24 25 1 5 3
2.60 8.75 10.
2.40 8.50 10.
2.25 8.25 10.
2.10 8.0 10.
2.05 7.75 10.
42 25 20 0 5 3
43 26 20 0 5 0
44 26 21 0 5 0
45 26 22 0 5 0
46 26 23 0 5 0
47 26 24 0 5 0
48 26 25 0 5 0
49 1 14 0 2 0
50 2 15 0 2 0
51 3 16 0 2 0
52 4 17 0 2 0
53 5 18 0 2 0
54 6 19 0 2 0
55 7 20 0 2 0
56 8 21 0 2 0
57 9 22 0 2 0
58 10 23 0 2 0
59 11 24 0 2 0
60 12 25 0 2 0
61 13 26 0 2 0
$ ELEMENTS GROSSIERS $
$ I NCGE SOMMETS NCGE NDSD $
1 7 1 2 8 7 14 15 21 20 7 1
2 7 2 3 9 8 15 16 22 21 7 1
3 7 3 4 10 9 16 17 23 22 7 1
4 7 10 11 5 4 23 24 18 17 7 1
5 7 5 6 12 11 18 19 25 24 7 1
6 7 1 7 12 6 14 20 25 19 7 1
7 6 7 8 13 20 21 26 6 2
8 6 8 13 9 21 26 22 6 2
9 6 13 9 10 26 22 23 6 2
10 6 13 10 11 26 23 24 6 2
11 6 13 11 12 26 24 25 6 2
12 6 7 13 12 20 26 25 6 2

Figure 3.5: Maillage 3D via COLIBR
L'exemple suivant montre une utilisation de COLIBH dans le cas où les données sont calculées, dans le programme, à partir d'un jeu réduit de paramètres. Suivent le programme d'appel du module qui utilise 2 sous-programmes et une vue du maillage obtenu sur la figure 3.6.
C ++++++++++++++++++++++++++++++++++++++++++++++
C TEST COLIBH ( COLIB2 AVEC UN SEUL HEXAEDRE )
C ----------- EXEMPLE DU JOINT ( PARTIE 1 )
C ++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 300000 )
COMMON M(LM)
INTEGER IDECAR(12),NBPARE(12)
REAL XYZ(3,8),XYZINT(3,200)
C
IMPRE = 3
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
C --- LA S.D.S. NOPO ---
NFNOPO = 10
NINOPO = 0
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'joint1.nopo','UNKNOWN,UNFORMATTED',2000000)
C --- LES REFERENCES ET LE SOUS DOMAINE ---
NDSDE = 1
IREF = 1
C ------------------------
C --- LA GEOMETRIE ---
C ------------------------
DO 1 I=1,3
DO 1 J=1,8
XYZ(I,J) = 0.
1 CONTINUE
C --- LES PARAMETRES DE DEFINITION :
RPI = 3.14159265
A30 = 30. * RPI / 180.
S30 = SIN(A30)
C30 = COS(A30)
R03 = 0.3
X03 = 0.
Y03 = 0.
R06 = 0.6
X06 = 0.
Y06 = 0.
BB = 1.2
C --- LA BASE :
XYZ(1,1) = R06 * S30
XYZ(1,2) = R06 * S30
XYZ(1,3) = R03 * S30
XYZ(1,4) = R03 * S30
XYZ(2,1) = - R06 * C30
XYZ(2,2) = R06 * C30
XYZ(2,3) = R03 * C30
XYZ(2,4) = - R03 * C30
C --- LE HAUT :
DO 2 I=1,2
DO 2 J=1,4
XYZ(I,J+4) = XYZ(I,J)
2 CONTINUE
DO 3 J=1,4
AA = 1.0 + 0.3 * XYZ(1,J) / 1.7
CALL SPELLI(AA,BB,XYZ(2,J+4),XYZ(3,J+4))
3 CONTINUE
C --- LES ARETES :
NPI = 5
DO 4 J=1,12
NBPARE(J) = NPI
IDECAR(J) = 0
4 CONTINUE
NBPARE(2) = 3
NBPARE(4) = 3
NBPARE(10) = 3
NBPARE(12) = 3
C
IDECAR(1) = 1
IDECAR(3) = 1
IDECAR(9) = 1
IDECAR(11) = 1
C --- LES POINTS INTERMEDIAIRES :
C ARETE 1 :
IEX11 = 1
IEX21 = 2
D1 = ( XYZ(2,IEX21) - XYZ(2,IEX11) ) / ( NPI + 1. )
C ARETE 3 :
IEX13 = 3
IEX23 = 4
D3 = ( XYZ(2,IEX23) - XYZ(2,IEX13) ) / ( NPI + 1. )
C Y
DO 5 J=1,NPI
XYZINT(2,J) = XYZ(2,IEX11) + J * D1
XYZINT(2,J+NPI) = XYZ(2,IEX13) + J * D3
5 CONTINUE
C X = FONCTION DE Y
DO 6 J=1,NPI
CALL SPCERC(R06,X06,Y06,XYZINT(2,J),XYZINT(1,J))
CALL SPCERC(R03,X03,Y03,XYZINT(2,J+NPI),XYZINT(1,J+NPI))
6 CONTINUE
C REPORT SUR ARETES 9 ET 11 :
DO 7 J=1,NPI
XYZINT(1,J+2*NPI) = XYZINT(1,J)
XYZINT(1,J+3*NPI) = XYZINT(1,J+NPI)
XYZINT(2,J+2*NPI) = XYZINT(2,J)
XYZINT(2,J+3*NPI) = XYZINT(2,J+NPI)
7 CONTINUE
C Z
DO 8 J=1,4*NPI
XYZINT(3,J) = 0.
8 CONTINUE
C Z ( ARETES 9 ET 11 )
DO 9 J=1,2*NPI
AA = 1.0 + 0.3 * XYZINT(1,J+2*NPI) / 1.7
CALL SPELLI(AA,BB,XYZINT(2,J+2*NPI),XYZINT(3,J+2*NPI))
9 CONTINUE
C --- APPEL DU MODULE ---
CALL COLIBH(M,NFNOPO,NINOPO,XYZ,IDECAR,NBPARE,XYZINT,IREF,NDSDE)
STOP
END
C ++++++++++++++++++++++++++++++++++++++++++++++
C SPCERC
C ++++++++++++++++++++++++++++++++++++++++++++++
SUBROUTINE SPCERC(R,A,B,Y,X)
RES = R*R - ( Y - B ) * ( Y - B )
X = A + SQRT( RES )
END
C ++++++++++++++++++++++++++++++++++++++++++++++
C SPELLI
C ++++++++++++++++++++++++++++++++++++++++++++++
SUBROUTINE SPELLI(A,B,Y,Z)
Z = SQRT( 1. - Y*Y / ( A*A ) )
END

Figure 3.6: Maillage 3D via COLIBH
L'exemple qui suit résulte de plusieurs appels de COLIBH, du recollement des maillages obtenus et de différentes manipulations géométriques de ce résultat (symétries, rotations, ... et recollement final)

Figure: Maillage d'un joint via COLIBH et transformations géométriques