![[BIG]](../icons/zoom18.gif){kind=icon}
![[Normal]](../icons/zoom14.gif){kind=icon}
![[small]](../icons/zoom10.gif){kind=icon}
Suiv.: Résolution par une méthode itérative Sup.: Résolution des systèmes linéaires Préc.: 1.1 Introduction Index Table des matières
Suiv.: Résolution par une méthode itérative
Sup.: Résolution des systèmes linéaires
Préc.: 1.1 Introduction
Index
Table des matières
Les méthodes présentées dans ce chapitre sont les trois méthodes classiques de résolution d'un système linéaire par factorisation de la matrice. On distingue donc successivement :
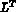, avec
L matrice triangulaire inférieure.
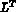, avec L matrice triangulaire inférieure à
diagonale unité, et D matrice diagonale.
Plusieurs versions de ces trois méthodes sont implémentées dans le code Modulef, suivant la place mémoire nécessaire au stockage de la matrice A.
Dans un premier temps, nous supposons que la matrice A peut être stockée intégralement en mémoire centrale, et nous décrivons précisément le stockage de la matrice et celui du second membre.
Pour plus de détails consulter le [Guide Modulef - 2].
Cette SD est l'organisation permettant de stocker, pour chaque ligne, les coefficients compris entre la première colonne de coefficient a priori non nul et la diagonale d'une matrice creuse de type "éléments finis". Ce type de stockage est dit profil ou skyline.
La SD MUA est composée de six tableaux dont l'organisation est prédéfinie.
Tableau MUA0 : Informations générales.
De type entier, ce tableau possède 32 variables. Il contient une description générale du travail (titre, date, nom), de la SD MUA (type, niveau, ...) et indique la présence ou non du tableau MUA1.
le titre du travail en 20 mots de 4 caractères,
la date de création en 2 mots de 4 caractères,
le nom du créateur en 6 mots de 4 caractères,
le type de la SD,
le paramètre de niveau de la SD,
un paramètre réservé,
le nombre de tableaux supplémentaires associés à la SD
(ils seront décrits dans le tableau MUA1).
Tableau MUA1 : Descripteur des éventuels tableaux supplémentaires.
Ce tableau est analogue au tableau B1 de la SD B (voir cette SD).
Tableau MUA2 : Description générale de la matrice.
Ce tableau de type entier contient 12 valeurs.
le type des coefficients de la matrice,
le nombre de blocs ou pages de la matrice,
le nombre de colonnes du plus grand bloc,
le nombre de mots nécessaires en m.c. pour stocker le plus grand bloc,
le nombre de matrices sur le fichier,
le type de stockage de la matrice,
la plus grande différence + 1 entre les numéros de 2 noeuds d'un même élément si NCODSA est non nul, 1 si NCODSA=0, c'est à dire la largeur de la demi-bande en terme de noeuds.
la plus grande différence + 1 entre les numéros des degrés de liberté de 2 noeuds d'un même élément si NCODSA est non nul, 1 si NCODSA=0, c'est à dire et la demi-largeur de bande en terme de degrés de liberté.
le nombre de degrés de liberté par noeud s'il est constant, 0 sinon,
le nombre de noeuds,
l'ordre de la matrice,
l'assemblage est réalisé si 1, n'a pas déjà été fait si 0.
Tableau MUA3 : Pointeur sur le dernier degré de chaque bloc.
Ce tableau est de type entier, de longueur NBLOC+1, il contient :
Tableau MUA4 : Pointeur sur le coefficient diagonal de chaque ligne.
Ce tableau est de type entier et de longueur NTDL+1 ou 2 selon NCODSA, il contient :
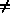0
Tableau MUA5 : Les coefficients de la matrice.
De type NTYP, ce tableau contient les coefficients de la matrice :
On considère la matrice d'ordre 12 suivante (les valeurs sont les rangs dans le stockage et non les coefficients de la matrice) formée de 3 pages :
Le tableau MUA5 de longueur MUA4(13) est subdivisé en 3 pages, ligne 1 à 5, 6 à 10 et 11 à 12. Chaque page a au plus 20 mots. Alors, on a :
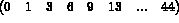
On considère la matrice d'ordre 12 suivante (les valeurs sont les rangs dans le stockage et non les coefficients de la matrice) composée de 3 pages :
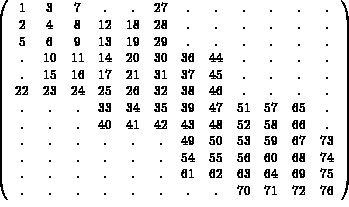
Ici, chaque page a au plus 13 mots. Alors, on a :
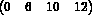
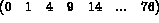
Dans le cas symétrique, on stocke la partie triangulaire inférieure
de la matrice A dans un
tableau monodimensionnel MUA5 ,
de la façon suivante : pour chaque variable i, on stocke tous les
coefficients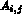 
de la ligne, avec mc(i) 
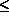j 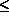i, (où mc(i) est
le plus petit indice de colonne tel que 
0). Ces coefficients (nuls ou non)
sont rangés par indice de colonne croissant. Les lignes sont ensuite
rangées par ordre de variable croissant dans le tableau MUA5.
Pour gérer la correspondance entre MUA5 et A, un pointeur MUA4 est
nécessaire, qui donne pour chaque ligne i l'adresse dans MUA5 du
coefficient diagonal 
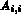. L'adresse ia dans MUA5 d'un coefficient
quelconque 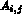est alors calculée par la formule
(![[note]](../icons/foot_motif.gif){kind=icon}
Avec la convention MUA4(1)=0)
Ce mode de stockage appelé stockage profil ou skyline, est particulièrement commode puisqu'il est aussi utilisable pour la matrice L. En effet les matrices A et L ont le même profil, et dans la pratique on les stocke souvent dans le même tableau.
Dans le cas non symétrique , on utilise la même forme de stockage, en
ajoutant les colonnes de la façon suivante :
pour chaque variable i, on stocke tous les
coefficients 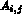de la ligne, avec 
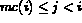, (où mc(i) est
le plus petit indice de colonne tel que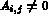 
). Ces coefficients (nuls ou non)
sont rangés par indice de colonne croissant; puis
on stocke tous les
coefficients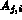 
de la colonne, avec mc(i) 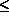j 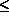i,
en finissant par le coefficient diagonal.
Ces informations sont ensuite
rangées par ordre de variable croissant dans le tableau MUA5.
Pour gérer la correspondance entre MUA5 et A, un pointeur MUA4 est
nécessaire, qui donne pour chaque variable i l'adresse dans MUA5 du
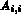coefficient diagonal . L'adresse ia dans MUA5 d'un coefficient
quelconque 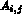est alors calculée par la formule
Cette SD est l'organisation choisie pour stocker un tableau de coefficients ayant la structure d'un vecteur (second membre d'un système, solution, etc.).
En pratique, le tableau, noté B, est de la forme B(NDSM,NTDL) où NDSM désigne par exemple le nombre de cas de charge ou de seconds membres et NTDL le nombre de degrés de liberté.
La SD B est composée de cinq tableaux dont l'organisation est prédéfinie.
Tableau B0 : Informations générales.
De type entier, ce tableau possède 32 variables. Il contient une description générale du travail (titre, date, nom), de la SD B (type, niveau, ...) et indique la présence ou non du tableau B1.
le titre du travail en 20 mots de 4 caractères,
la date de création en 2 mots de 4 caractères,
le nom du créateur en 6 mots de 4 caractères,
le type de la SD,
le paramètre de niveau de la SD,
un paramètre réservé,
le nombre de tableaux supplémentaires associés à la SD
(ils seront décrits dans le tableau B1).
Tableau B1 : Descripteur des éventuels tableaux supplémentaires.
Ce tableau de type entier existe si NTACM (cf. B0) est non nul. Il contient, pour chaque tableau à décrire, 22 variables. En règle générale, il n'y a pas de tableaux associés sauf pour certaines applications où l'on a besoin de conserver dans la SD des valeurs n'entrant pas dans le cadre de sa définition standard.
Si le tableau B1 existe, il contient séquentiellement :
Boucle i de 1 à NTACM
Tableau B2 : Description générale du tableau de coefficients.
Ce tableau de type entier contient 11 valeurs.
le type du tableau B4,
le nombre de ses indices (fixé à 2),
la valeur maximale de son second indice (par exemple NTDL si B4 n'a qu'une page),
le code de découpage en blocs du tableau B4 avec :
le nombre de blocs,
le nombre de noeuds,
le nombre de tableaux B4 lorsque la SD est sur fichier,
le nombre de degrés de liberté par noeud s'il est constant, 0 sinon,
le nombre de degrés de liberté ou la valeur maximale du second indice du tableau B4 lorsque les NBLOC blocs sont considérés,
le code de stockage du tableau B4 avec :
Tableau B3 : Pointeur sur les blocs.
Ce tableau de type entier contient NBLOC+1 variables indiquant la segmentation du tableau B4.
Tableau B4 : Les coefficients du(des) tableau(x).
De type NTYP ce tableau contient les NDSM*M2 valeurs de chaque page.
) à B4(NDSM, 
).
= NDL(B3(i+1)+1) où NDL est le nombre de degrés de liberté par
noeuds.
Cet ensemble de 5 tableaux (B0, B1, B2, B3 et B4) gérés par quelques sous-programmes, contient les NDSM seconds membres (ou les solutions) d'un système linéaire A x = b. Les coefficients du tableau B4(NDSM,NTDL) représentent les NTDL composantes des NDSM seconds membres du système linéaire à résoudre. Après résolution, les solutions du système linéaire sont aussi rangés dans un tableau B4 (le même, ou celui d'une structure B distincte).