




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: La méthode de décomposition de
Sup.: Liste des méthodes itératives
Préc.: 2.1 Les modules
Index
Table des matières
Il peut être intéressant d'utiliser directement les algorithmes, en particulier pour écrire
une procédure nonl inéaire efficace. A chaque module correspondent deux programmes : un en simple précision et un
en double précision. En principe, les noms de ces deux programmes diffèrent uniquement par la dernière lettre :
R en simple précision (bibliothèque RESR), D en double précision (bibliothèque RESD).
- Assemblage de la matrice
- ASGC1D assemblage d'une matrice symétrique ou non, en double précision
- ASGC1R assemblage d'une matrice symétrique ou non, en simple précision
- Assemblage du second membre
- ASSBPD assemblage du second membre en double précision (structure B en mémoire secondaire)
- ASSEBD assemblage du second membre en double précision (structure B en mémoire centrale)
- ASSMBD assemblage vectoriel du second membre en double précision
- ASSBPR assemblage du second membre en simple précision (structure B en mémoire secondaire)
- ASSEBR assemblage du second membre en simple précision (structure B en mémoire centrale)
- ASSMBR assemblage vectoriel du second membre en simple précision
- Prise en compte des conditions aux limites
- CLGC1D conditions aux limites de type
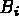 = V en double précision
= V en double précision
- CLGC2D conditions aux limites en relation linéaire en double précision
- CLGC1R conditions aux limites de type
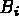 = V en simple précision
= V en simple précision
- CLGC2R conditions aux limites en relation linéaire en simple précision
- Résolution par méthode itérative
- Factorisation incomplète (calcul de la matrice de préconditionnement)
- CDLL1D factorisation incomplète de Cholesky en double précision
- CDLL2D factorisation incomplète de Crout en double précision
- CDLU1D factorisation incomplète de Gauss en double précision
- CDLL1R factorisation incomplète de Cholesky en simple précision
- CDLL2R factorisation incomplète de Crout en simple précision
- CDLU1R factorisation incomplète de Gauss en simple précision
- Résolution par itérations de gradient conjugué
- DGRA1D double gradient conjugué accéléré avec préconditionnement Gauss incomplet en double précision
- ICHR1D gradient conjugué avec préconditionnement Cholesky / Crout incomplet en double précision
- GCDIAD gradient conjugué avec préconditionnement diagonal en double précision
- SIMGCD gradient conjugué sans préconditionnement en double précision
- SSOR1D gradient conjugué avec préconditionnement SSOR en double précision
- DGRA1R double gradient conjugué accéléré avec préconditionnement Gauss incomplet en simple précision
- ICHR1R gradient conjugué avec préconditionnement Cholesky / Crout en simple précision
- GCDIAR gradient conjugué avec préconditionnement diagonal
en simple précision
- SIMGCR gradient conjugué sans préconditionnement en simple précision
- SSOR1R gradient conjugué avec préconditionnement SSOR
en simple précision
- Résolution du système linéaire de préconditionnement
- DRCHID préconditionnement par Cholesky incomplet en double précision
- DRCRID préconditionnement par Crout incomplet en double précision
- DGRA1D préconditionnement par Gauss incomplet en double précision
- SSOR2D préconditionnement par la matrice SSOR en double précision
- DRCHIR préconditionnement par Cholesky incomplet en simple précision
- DRCRIR préconditionnement par Crout incomplet en simple précision
- DGRA1R préconditionnement par Gauss incomplet en simple précision
- SSOR2R préconditionnement par la matrice SSOR en simple précision






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: La méthode de décomposition de
Sup.: Liste des méthodes itératives
Préc.: 2.1 Les modules
Index
Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
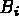 = V en double précision
= V en double précision
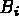 = V en simple précision
= V en simple précision