Suiv.: 1.2 Formulations variationnelles Sup.: Le problème de la thermique Préc.: Le problème de la thermique Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 1.2 Formulations variationnelles
Sup.: Le problème de la thermique
Préc.: Le problème de la thermique
Index
Table des matières
La formulation de ce problème en équations aux dérivées partielles (E.D.P.) est donnée ci-dessous :
avec
 le flux de température
le flux de température
 le produit de la masse thermique par la chaleur massique,
le produit de la masse thermique par la chaleur massique,
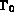 ,
,
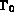 ,
,
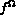 la puissance volumique appliquée à
la puissance volumique appliquée à

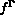 le flux appliqué sur
le flux appliqué sur 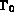 ,
,
 la température imposée sur
la température imposée sur 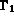 ,
,
 la température initiale (t=0),
la température initiale (t=0),