Suiv.: 7.2 Le fichier POBA Sup.: Données Préc.: Données Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 7.2 Le fichier POBA
Sup.: Données
Préc.: Données
Index
Table des matières
Pour décrire ces données, nous nous plaçons dans le cas d'un problème d'élasticité tridimensionnel isotrope. Ainsi les valeurs caractérisant la physique du problème sont constituées de :
 la masse volumique du matériau utile pour calculer
la masse volumique du matériau utile pour calculer 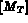 , les matrices
élémentaire de masse,
, les matrices
élémentaire de masse,
 le module de Young et le coefficient de Poisson du matériau, utiles pour
calculer
le module de Young et le coefficient de Poisson du matériau, utiles pour
calculer 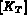 , les matrices
élémentaire de rigidité (dans le cas anisotrope les données sont les
coefficients de la matrice d'élasticité caractéristique du matériau étudié).
E et
, les matrices
élémentaire de rigidité (dans le cas anisotrope les données sont les
coefficients de la matrice d'élasticité caractéristique du matériau étudié).
E et  sont utiles également pour
calculer les
sont utiles également pour
calculer les 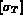 , matrices élémentaire de contraintes (même remarque),
, matrices élémentaire de contraintes (même remarque),
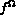 et
et 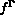 les forces s'exerçant dans
les forces s'exerçant dans  et sur
et sur 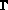 qui
permettent de calculer les
qui
permettent de calculer les 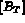 , seconds membres élémentaires.
, seconds membres élémentaires.
Les données, en règle générale, peuvent être fournies suivant deux options:
Quelque soit le cas, elles seront classées, et donc fournies, par volume 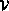 , surface
, surface 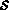 ,
ligne
,
ligne 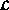 ou point
ou point  . La plupart des éléments suivent cette classification
(avec éventuellement l'absence d'une ou de plusieurs de ces catégories).
. La plupart des éléments suivent cette classification
(avec éventuellement l'absence d'une ou de plusieurs de ces catégories).
Pour une catégorie donnée, on distingue deux types de lots de valeurs :
Par exemple, pour la catégorie 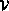 , les données concernent
, les données concernent  qui se
répartissent comme on l'a déjà vu en
qui se
répartissent comme on l'a déjà vu en  pour la masse, le couple E,
pour la masse, le couple E,  pour la rigidité et
pour la rigidité et
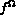 pour le second membre.
pour le second membre.
Par ailleurs le calcul des quantités élémentaires se fait, élément par élément, dans l'ordre suivant:
Les données relatives aux calculs des matrices et des contraintes sont décrites dans la partie MILI, celles relatives aux calculs des seconds membres le sont dans la partie FORC. Ainsi, si on désire calculer:
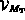 ,
,  de la partie MILI et
de la partie MILI et  ,
, 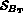 de la partie FORC,
de la partie FORC,
 de la partie MILI et
de la partie MILI et  ,
, 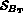 de la partie FORC,
de la partie FORC,
 et
et 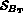 de la partie FORC,
de la partie FORC,
 , E,
, E,  dans MILI et
dans MILI et 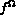 ,
, 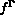 dans FORC
dans FORC
 dans MILI et
dans MILI et 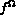 ,
, 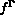 dans FORC
dans FORC
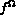 ,
, 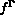 dans FORC
dans FORC
Concernant les données relatives à un calcul (par exemple celui d'un second membre), les valeurs à fournir à l'élément fini ont été définies par le créateur de ce dernier. Les fiches techniques de chaque élément précisent ce point, c'est-à-dire la nature, le nombre et l'ordre des valeurs à fournir. Dans notre exemple, on a généralement l'ordre suivant f(1:NDSM,1:NDIM,1:NPI) (au sens d'un tableau Fortran):
Ainsi, pour 2 cas de charge, dans le cas d'une intégration par la formule de Simpson, pour un élément 2D, les
valeurs attendues au niveau de 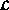 sont dans l'ordre les suivantes:
sont dans l'ordre les suivantes:
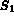 , extrémité 1 de l'arête concernée) :
, extrémité 1 de l'arête concernée) :
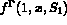 ,
, 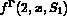 ,
, 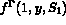 ,
, 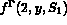
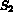 , extrémité 2 de l'arête concernée) :
, extrémité 2 de l'arête concernée) :
 ,
, 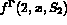 ,
, 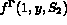 ,
, 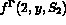
 de l'arête concernée) :
de l'arête concernée) :
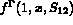 ,
,  ,
, 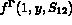 ,
, 
Ces valeurs, comme toute valeur à fournir, peuvent être effectivement rentrées de différentes manières:
[Guide Modulef - 4] décrit en détails ce point.