




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: tetr3p1d
Sup.: 9 Fiches techniques
Préc.: quad2q1d
Index
Table des matières
Bibliothèque '
Elasticité' -
Elément fini:
QUAD 2Q2C
P.L. George, INRIA
DESCRIPTION DE L'ELEMENT
- Dimension de l'espace : 2, élément bidimensionnel
- Inconnues :
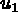 et
et 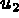 , les déplacements suivant x et y
, les déplacements suivant x et y
- Formulation variationnelle : en 'déplacements'
- Numéro de code : 200 008
- numéro de code géométrique : 4 (quadrangle)
- Interpolation :
 -Lagrange isoparamétrique
-Lagrange isoparamétrique
- Nombre de points : 8
- Nombre de types de points : 1
- Les points sont définis par leurs seules coordonnées : NCACAR=0
- Nombre de noeuds : 8
- Nombre de types de noeuds : 1
- Type des noeuds : les sommets et les milieux des arêtes, 2 d.l. par noeud, 'VN' pour
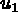 et pour
et pour 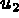
- Points et noeuds coïncident partout : NCOPNP=1
- Fichier POBA : nécessaire
- Blocage (S.D. BDCL) :
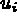 (noeud) = valeur
(noeud) = valeur
- Sous-programmes utilisateurs : oui
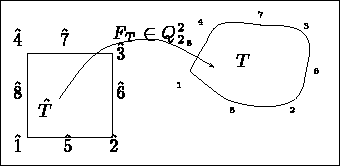
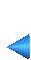
Figure: Elément QUAD 2Q2C
Coordonnées sur l'élément de référence:
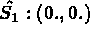
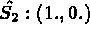
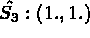
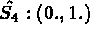


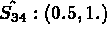
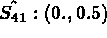
INTEGRATION NUMERIQUE
- -
- Intégration de surface: Intégration numérique à 9 points (Gauss).
- npis=9
-
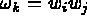 pour i,j=1,3
pour i,j=1,3
avec 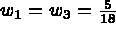 et
et 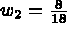
-
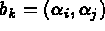 pour i,j=1,3
pour i,j=1,3
avec 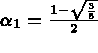 ,
, 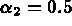 et
et
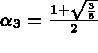
- -
- Intégration de bord: Intégration numérique de Simpson.
- npil=3
-
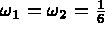 et
et 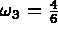
-
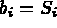 pour i=1,2 les extrémités de l'arête et
pour i=1,2 les extrémités de l'arête et 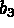 le milieu de celle-ci
le milieu de celle-ci
LES DONNEES A FOURNIR (en double précision)
- -
- S.D. MILI:
- -
- S.D. FORC: NDSM seconds membres.
- terme de surface
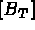 , partie
, partie 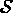
-
 pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
- terme de bord
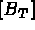 , partie
, partie 
-
 pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.
Remarques
-
Pour utiliser les sous-programmes utilisateurs, on fixera la valeur de NOTEL à la valeur ci-dessus en
ajoutant 20 en isotrope (en retranchant 20 en anisotrope). Cette valeur est demandée lors de la
construction des S.D. MILI ou FORC (cf [Guide Modulef - 4]).
- Le fichier POBA est organisé comme suit (tableau 2Q25, 231 valeurs):
- NDIM,NBPOLY,NPIS,1,1,1 i.e la dimension de l'espace, le nombre de polynômes de base (8),
le nombre de points d'intégration et trois indicateurs (6 valeurs),
-
 (9 valeurs),
(9 valeurs),
- [P] les valeurs des polynômes aux points d'intégration (72 valeurs),
- [DP] les valeurs des dérivées des polynômes aux points d'intégration (144 valeurs).
- Pour calculer les coordonnées des points d'intégration sur l'élément courant, on pourra
utiliser la formule:
où
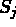 est le noeud j et
est le noeud j et  est la valeur du polynôme j au point k.
est la valeur du polynôme j au point k.






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: tetr3p1d
Sup.: 9 Fiches techniques
Préc.: quad2q1d
Index
Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
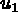 et
et 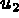 , les déplacements suivant x et y
, les déplacements suivant x et y
 -Lagrange isoparamétrique
-Lagrange isoparamétrique
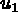 et pour
et pour 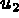
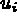 (noeud) = valeur
(noeud) = valeur
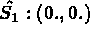
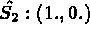
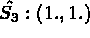
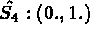


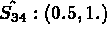
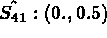
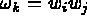 pour i,j=1,3
pour i,j=1,3 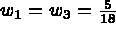 et
et 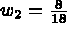
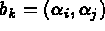 pour i,j=1,3
pour i,j=1,3 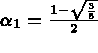 ,
, 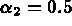 et
et
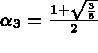
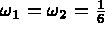 et
et 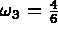
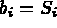 pour i=1,2 les extrémités de l'arête et
pour i=1,2 les extrémités de l'arête et 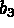 le milieu de celle-ci
le milieu de celle-ci
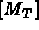 , partie
, partie 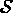
 la masse volumique supposée constante par élément.
la masse volumique supposée constante par élément.
 , partie
, partie 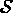
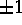 ), en déformations planes (
), en déformations planes (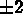 ).
).

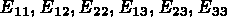
 si elle n'est pas calculée, rien sinon.
si elle n'est pas calculée, rien sinon.
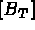 , partie
, partie 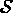
 pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
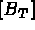 , partie
, partie 
 pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.
 (9 valeurs),
(9 valeurs),
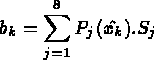
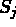 est le noeud j et
est le noeud j et  est la valeur du polynôme j au point k.
est la valeur du polynôme j au point k.