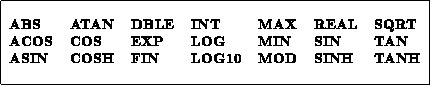




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 2.2 Programming
Up: 2 Function interpreter
Prev: 2 Function interpreter
Index
Contents
The function definitions are given in free format
(chapter 1), may be split over several lines, and appears between columns 1 and 72, inclusively.
The general form is given below:
Function(parameter1, parameter2, ...) = expression ;
For example:
F(X,Y,Z) = (X-X**3) * (Y-Y**3) * (Z-Z**3)
+ LOG(X+Y+Z+1)
- 5.9 ;
As illustrated above, blanks are admissible and the function definition is terminated by a semi-colon (;)
This format is quite natural and simple expressions should not
present any difficulty.
In order to take care of more complicated cases, two different presentations are
given below:
The first corresponds to the Fortran 77 format;
the second is more formal.
The format is very similar to that of
"statement functions" in Fortran 77, with the following differences:
- The definition may start before column 7.
- If the definition is split over several lines, it suffices to write it one line after the other, without
forgetting the final semi-colon (;). There is not, as in Fortran, the
"continue character" in column 6.
- All operands are considered as REAL
(real single precision): parameters (whatever the first letter of the identifier may be)
and numerical constants (36 and 36. are equivalent, and 1/2 returns 0.5).
- In Fortran, all operators with the same priority are evaluated from left to right,
except exponentials. Here, there is no exception:
A**B**C is evaluated as (A**B)**C.
- Intrinsic function names are reserved, and cannot therefore be employed to
identify a parameter. The list of reserved identifiers is given in
figure 2.1.
- A certain number of extensions are authorized. For example, the length of identifiers
may exceed 6 characters
(section 2.1.2).
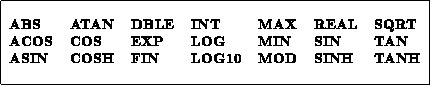
Figure 2.1: The reserved identifiers
Consider again the general format (section 2.1):
Function(parameter1, parameter2, ...) = expression ;
The above syntax is symbolized by the diagram in figure
2.2.
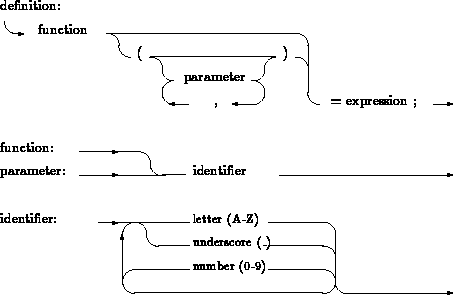
Figure 2.2: Diagram of the function definition
- identifier
- is a non-empty sequence of letters (A-Z),
underscore characters (_) and numbers (0-9). The first character must be a letter
or an underscore character. The length of an identifier is only limited
by the length of an input line, i.e. 72 characters.
The syntax analyzer is responsible for checking that all identifiers differ from reserved words
(figure 2.1).
- function
- is the identifier of the function to be defined, assumed
to be single precision real.
- parameter1, parameter2, ...
- are the identifiers of the formal parameters
to be evaluated in the expression, assumed to be single precision real.
- expression
- is a construction consisting of operands, operators and
parentheses, which returns a single precision real value.
The operands are parameters or numeric constants.
The list of operators available is given in the following section.
- a semi-colon
- terminates the complete function.
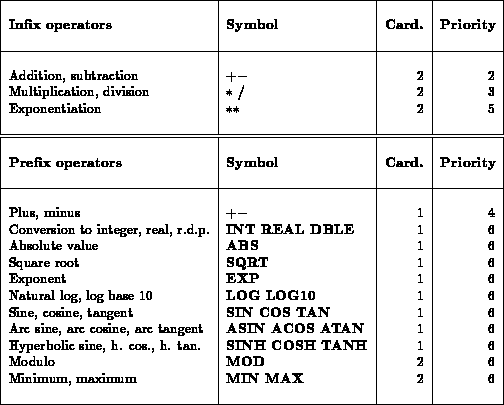
Figure 2.3: Priorities of operators
Figure 2.3 gives the cardinality and priority of each prefix and infix operator:
- By definition, an infix operator is placed between the two operands on
which it operates; a prefix operator is placed before the operand(s) on which it
operates. In this manner, we write:
A*B -A ABS A MOD A B
The format operator(operand1, operand2, ...),
which is more usual and which furthermore exhibits the evaluation order better, is also permitted:
ABS(X) MOD(X*Y, Z)
- The cardinality relates to the number of operands
(2 for infix operators).
- The priority determines the evaluation order of an expression or a sub-expression, in the
absence of parentheses:
- If two operators have different priorities, the one with the highest priority
is evaluated first.
- If two infix operators have the same priority,
the one on the left is evaluated first.
- If two prefix operators have the same priority,
the one on the right is evaluated first.
A few examples are given below to illustrate the priorities assumed.
|
A+B*C | is evaluated as | A+(B*C) |
|
A/B*C | is evaluated as | (A/B)*C |
|
A**B**C | is evaluated as | (A**B)**C |
|
-A+B | is evaluated as | (-A)+B |
|
-A**B | is evaluated as | -(A**B) |
|
SIN COS A | is evaluated as | SIN(COS(A))) |
In order to optimize on run time and computational precision, certain exponentials are replaced
automatically by multiplications.
Therefore, do not hesitate to type (X+1)**2 rather than (X+1)*(X+1)!






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 2.2 Programming
Up: 2 Function interpreter
Prev: 2 Function interpreter
Index
Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()