Next: 1.4 Solution by domain decomposition Up: 1 Solution of linear systems Prev: 1.2 Solution by a direct method Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Next: 1.4 Solution by domain decomposition
Up: 1 Solution of linear systems
Prev: 1.2 Solution by a direct method
Contents
The methods presented in this chapter are classical methods, of conjugate gradient type, for the solution of linear systems. We can distinguish between:
The first method is implemented in the MODULEF code with three different preconditioning techniques. The matrix is stored in an AMAT type data structure.
For more details consult [MODULEF User Guide - 2].
This DS is used to store the non-zero coefficients of a "finite element" type rectangular or square sparse matrix. This type of storage is called compact storage.
The DS AMAT is composed of seven arrays of predefined order.
This integer array contains 32 variables, giving a description of the job (title, date, name), of the DS AMAT (type, level, ...), and indicates the presence (or absence) of array AMA1:
the job title in 20 words of 4 characters (stored in integers),
the creation date in 2 words of 4 characters (ditto),
the name of the creator in 6 words of 4 characters (ditto),
the DS type,
the DS level,
a reserved parameter,
the number of supplementary arrays corresponding to the DS.
(they are described in array AMA1).
This array is analogous to array B1 of DS B (see this DS).
This integer array contains 10 values:
matrix order,
the type of matrix coefficients,
the number of a priori non-zero matrix coefficients,
the number of words necessary in M.M. to store arrays AMA5 and AMA6,
the number of pages for the matrix (if secondary memory is used),
the type of matrix storage:
the number of degrees of freedom per node if it is constant, or 0,
the number of nodes,
the number of matrices assembled and stored in S.M. (if 0: AMA5 exists but AMA6 is absent),
the type of matrix factorization,
This integer array of NPAGE + 1 words contains:
This integer array of NTDL + 1 (or 2) words in length contains:
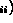 of the diagonal coefficient A
of the diagonal coefficient A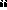 (points
therefore to AMA5 and AMA6)
(points
therefore to AMA5 and AMA6)
This integer array contains NTCOEF words if NCODSA 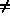 0 and 0 words if not:
0 and 0 words if not:
This array of type NTYP contains the NTCOEF non-zero matrix coefficients:
Consider the 9-th order matrix shown below (the values indicated correspond to the rows of the matrix storage and not matrix coefficients):
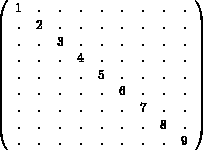
Thus, we have:
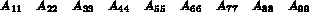
Consider the following 9-th order matrix (the values indicated correspond to the rows of the matrix storage and not to the matrix coefficients):

Thus, we have:
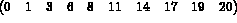


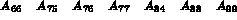
The correspondence between arrays AMA3, AMA4 and AMA5, therefore the position of the matrix coefficients in array AMA6, is illustrated in figure 1.1.
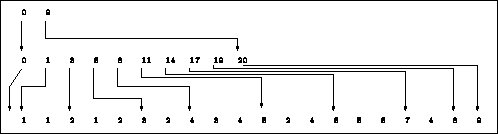
Figure 1.1: Correspondence for example 2
Consider the following 9-th order matrix (the values indicated correspond to the rows of the matrix storage and not to the matrix coefficients):

Thus, we have:
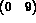
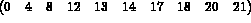
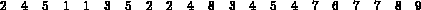
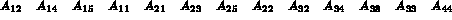
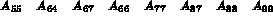
The correspondence between arrays AMA3, AMA4 and AMA5, therefore the positions of the matrix coefficients in array AMA6, is illustrated in figure 1.2.
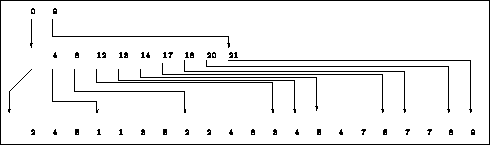
Figure 1.2: Correspondence for example 3
For the symmetric case , matrix A
is stored in a one-dimensional array AMAT6 as follows:
for each row i, we only retain the non-zero coefficients 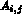 ,
for
,
for 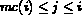 (
(![]() see the description of D.S. MUA
for the definition of mc(i)), ordered according to increasing index of column j.
The rows are therefore ordered in increasing order in AMAT6.
To manage the correspondence between AMAT6 and
A, pointer AMAT4 is used to indicate the address of the last non-zero coefficient
see the description of D.S. MUA
for the definition of mc(i)), ordered according to increasing index of column j.
The rows are therefore ordered in increasing order in AMAT6.
To manage the correspondence between AMAT6 and
A, pointer AMAT4 is used to indicate the address of the last non-zero coefficient 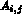 in
AMAT6 for each row i.
Lastly, pointer AMAT5 of the same size as AMAT6, and ordered in a coherent manner, gives the corresponding index of column j
for each coefficient
in
AMAT6 for each row i.
Lastly, pointer AMAT5 of the same size as AMAT6, and ordered in a coherent manner, gives the corresponding index of column j
for each coefficient 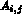 .
We therefore only store the non-zero coefficients of matrix A. Address ia in AMAT6 of an arbitrary coefficient
.
We therefore only store the non-zero coefficients of matrix A. Address ia in AMAT6 of an arbitrary coefficient 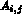 is not
accessible directly, and it is necessary to search for the column j's index in
AMAT5 between addresses AMAT4(i)+1 and AMAT4(i+1).
is not
accessible directly, and it is necessary to search for the column j's index in
AMAT5 between addresses AMAT4(i)+1 and AMAT4(i+1).
For the non-symmetric case , we adopt the same form of storage, i.e. we keep all the non-zero coefficients of the complete row, by ordering them by increasing column index, with the exception of the diagonal coefficient, placed at the end of the row.
This storage mode is called compact storage , also called Morse storage in MODULEF.