



![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 3 The domain decomposition method
Up: 2 Iterative methods
Prev: 2.1 The modules
Contents
It could be interesting to use the algorithms directly, in particular to write an efficient
non-linear procedure. Two programs correspond to each module:
one in single precision and one in
double precision.
In principle, the names of the two programs differ only in the last letter:
R in single precision (library RESR), D in double (library RESD).
- Matrix assembly
- ASGC1D assembly of a symmetric or non-symmetric matrix in double precision,
- ASGC1R assembly of a symmetric or non-symmetric matrix in single precision.
- Assembly of the right-hand-side
- ASSBPD assembly of the RHS in double precision (structure B in secondary memory),
- ASSEBD assembly of the RHS in double precision (structure B in main memory),
- ASSMBD vectorial assembly of the RHS in double precision,
- ASSBPR assembly of the RHS in single precision (structure B in secondary memory),
- ASSEBR assembly of the RHS in single precision (structure B in main memory),
- ASSMBR vectorial assembly of the RHS in double precision.
- Impose the boundary conditions
- CLGC1D boundary conditions of type
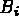 = V in double precision,
= V in double precision,
- CLGC2D boundary conditions i.t.o. linear relations in double precision,
- CLGC1R boundary conditions of type
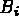 = V in single precision,
= V in single precision,
- CLGC2R boundary conditions i.t.o. linear relations in single precision.
- Solution by iterative method
- Incomplete factorization (computation of the preconditioning matrix)
- CDLL1D incomplete Cholesky factorization in double precision,
- CDLL2D incomplete Crout factorization in double precision,
- CDLU1D incomplete Gauss factorization in double precision,
- CDLL1R incomplete Cholesky factorization in single precision,
- CDLL2R incomplete Crout factorization in single precision,
- CDLU1R incomplete Gauss factorization in single precision.
- Solution conjugate gradient iterations
- DGRA1D accelerated double conjugate gradient with incomplete Gauss preconditioning in double precision,
- ICHR1D conjugate gradient with incomplete Cholesky/Crout preconditioning in double precision,
- GCDIAD conjugate gradient with diagonal preconditioning in double precision,
- SIMGCD conjugate gradient without preconditioning in double precision,
- SSOR1D conjugate gradient with SSOR preconditioning in double precision,
- DGRA1R accelerated double conjugate gradient with incomplete Gauss preconditioning in single precision,
- ICHR1R conjugate gradient with Cholesky/Crout preconditioning in single precision,
- GCDIAR conjugate gradient with diagonal preconditioning
in single precision,
- SIMGCR conjugate gradient without preconditioning in single precision,
- SSOR1R conjugate gradient with SSOR preconditioning
in single precision.
- Solution of a preconditioned linear system
- DRCHID incomplete Cholesky preconditioning in double precision,
- DRCRID incomplete Crout preconditioning in double precision,
- DGRA1D incomplete Gauss preconditioning in double precision,
- SSOR2D preconditioning by matrix SSOR in double precision,
- DRCHIR incomplete Cholesky preconditioning in single precision,
- DRCRIR incomplete Crout preconditioning in single precision,
- DGRA1R incomplete Gauss preconditioning in single precision,
- SSOR2R preconditioning by matrix SSOR in single precision.





![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 3 The domain decomposition method
Up: 2 Iterative methods
Prev: 2.1 The modules
Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
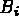 = V in double precision,
= V in double precision,
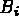 = V in single precision,
= V in single precision,