To exploit mathematical models in order to simulate, evaluate, diagnose and manage in an optimal manner complex systems (see applications).
in order to estimate non metered quantities, to take advantage of possible redundancy in measurements in order to remove measurement errors, to detect abnormal states, to locate failures, etc.
![]() Back to the list of contents (without frames)
Back to the list of contents (without frames)
The use of finite element methods for the discretization of
is one of our present research activity.
For differential equations, the general idea is as follows:
The quality of approximation depends essentially upon the family of finite elements which were retained and its adaptation to the considered problem. In this matter, the specific features of certain differential equations (as in Mechanics for example) suggest a customized choice for each type of variable.
For optimal control problems in continuous time, the general idea is similar, but one manages to follow the same approach for all variables, including dual variables (co-states, constraint multipliers, etc.) and for all equations and constraints showing up in the problem formulation; finally, the test functions related to primal equations coincide in general with finite elements related to dual variables, and vice-versa. With this way of dealing with discretization, one succeeds in reconciliating two points of view which generally yield different results when using other discretization methods:
One aim of this project is to provide a specialized toolbox in the Scilab framework (freeware distributed by INRIA).
![]() Back to the list of contents (without frames)
Back to the list of contents (without frames)
The purpose here is to overcome difficulties which arise from the enormous size of problems to be solved by taking advantage of the structure of large-scale systems which are generally not monolithic.
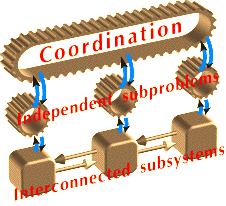
This is the other way of overcoming the difficulty arising from the large scale; its consists in representing several variables by a single one, provided that, for example, these variable dynamics are homogeneous. From this point of view, aggregation is a complementary idea of decomposition since homogeneity is more likely to be effective inside subproblems than at the global level. Aggregation must be paired with disaggregation which at least provides a solution satisfying all problem constraints, even if it is not exactly optimal.
Most encountered applications involve random phenomena (failures, weather, demands...), which requires an adequate formulation.
Some variance reduction techniques for the estimator so obtained have been proposed in the case of "scaled" probabilities (for example, in the situation of failure of various equipments, the probability of a single breakdown being small, say, of order epsilon, the situations without any failure are of probability close to one, the situations with a single failure are of probability of order epsilon, those with two breakdowns are of order epsilon to the square, etc.).
All these ideas have been combined with the techniques of decomposition/coordination in order to solve large-scale static stochastic optimization problems.
A technique of scenario trees has been proposed in order to extend decomposition/coordination techniques to the framework of dynamic stochastic optimization, at least for certain problems for which some "separation principle" is satisfied (this already covers a good deal of practical applications). Roughly speaking, the idea is to discretize the underlying probability space (with the scenarios) while preserving, in the discrete formulation, essential notions pertaining to information structure which enables one to express, for example, the causality of control strategies (present decisions should not depend on future observations).
In twenty five years of existence of this project, one can classify the main industrial applications that have been dealt with in three general categories, but some applications are in fact relevant to two, and sometimes to the three, categories.
There exists in France several water supply networks at the regional scale (they were built up progressively, by interconnection of local networks). The trend is nowadays to control these networks from a unique remote control center where all available measurements are concentrated with help of a teletransmission network, and from which all main control decisions taken by a human operator, only assisted by some local automata, are issued. The result of this situation is that the operator must face a more and more involved picture in which he plays the role of the brain of a sprawling system permitted by modern "teletechnology".
The aim of our studies have been to devise computer tools to assist the human operator in his decision-making process. The problem can be formulated as a classical optimal control problem. But, apart from the obvious presence of uncertainties (demands can be predicted, but with limited precision), this problem is very complex since the dynamic system (namely, the network composed of reservoirs, pipes, control devices -- valves, pumps --, water production plants etc.) is described by an implicit nonlinear mathematical model which is very cumbersome to handle for dynamic optimization purposes. The cost function is made up of the electric power bill (the price of electricity changes with time periods within the 24 hours, with unfortunately peak hours which coincide with water consumption peaks) and of the marginal water treatment cost (which varies geographically according to the water resource origins). Therefore, one faces a large-scale allocation problem of the production in space and time (subject to various operational constraints).
Thanks to a clever combination of decomposition/coordination and aggregation techniques, a problem involving about twenty state variables (reservoirs) was solved satisfactorily with a computational time, on a standard workstation, quite compatible with a daily operation of the software.
Beyond the non negligible savings that a daily use of this software provides with regard to operational costs, the rational long term expansion of such networks (investment decisions regarding the building of new reservoirs and pipes, contract negotiations with suppliers and customers, etc.) which is made possible by the same software can generate even more substantial savings.
In Paris, water supply networks run in the same galleries as sewers. Thus, a major leak due to pipe breaking may remain unnoticed for a long time, which forces operators to organize rounds in these galleries. Hence, the idea is to try to exploit all available measurements, as well as network mathematical models (qualitatively and quantitatively), in order to detect those leaks as soon as they appear and to locate them as accurately as possible.
The first issue in this problem is that of observability of the quantities one tries to monitor given the available measurements; namely, the question is: does one have enough mathematical relations between measurements and variables for the availability of the former (possibly over some time period) to be sufficient to estimate the latter? This is a difficult algebraic problem for networks obeying Kirchhoff and Ohm laws.
Once observable variables have been determined, the next issue is to estimate them numerically and in real time if possible. Then, by looking at their dynamic evolution, one tries to detect abnormal variations, and finally one attempts to geographically locate the source of the trouble.
A software has been devised to bring an answer to these various issues. In particular, at the design stage of a measurement system, or when considering its expansion, this software can help in positioning new sensors which "maximize system observability", that is, the investment efficiency.
Experiments conducted on some part of the Paris network have shown
the effective possibility of detecting and locating, with a
satisfying precision, three simultaneous leaks artificially
introduced by night by opening fire hydrants.
District heating networks operating with pressurized water are made up of heating stations burning various fuels (fossil fuels, garbage, etc., possibly using geothermal water as another heat resource) and of a tree-shaped or meshed graph of double pipes (one pipe conveying the hot water from heat stations to consumer substations, the other pipe bringing back the water which went through heat exchangers back to the stations). The control of such networks amounts essentially to choosing the pump speeds forcing water circulation and the temperature of outgoing water from heat stations. These decisions have two consequences:
In addition, the operation of each heating station must be optimized with respect to the repartition of the global production among the various operational boilers by taking their efficiency curves into account. As it can be realized, the global management of such district heating networks is rather complex and the economic incidence is important because those networks are huge energy "eaters".
Several pieces of software for simulation and optimization (computer-aided decision for designers and operators) have been produced, both for steady-state or slowly varying operation, and for transient behavior; the latter occurs in particular in the morning peak hour, when the network demand abruptly increases by passing from the night to the day regime, for building heating and for industrial needs as well. In this case, the non negligible time required by hot step propagation through networks sometimes spreading over tens of kilometers causes delays which make phenomena not entirely intuitive. This has been realized through the systematic dynamic optimization of transient regimes based on nonlinear hyperbolic partial differential equation models.
Large petrochemical plants encompass a power station which supplies steam at different pressure levels to chemical production units together with electric power (the rest of the plant electric power consumption being provided by EDF). These various utilities are generally produced by several boilers and turbo-alternators, the latter converting high pressure level steam to lower pressure levels while recovering the corresponding energy to produce electricity. The possible surplus of steam production is simply discharged in the atmosphere since it cannot be stored.
Economic data pertaining to the management of such power stations are rather numerous: efficiency curves of boilers and alternators, fuel costs, EDF contracts, etc. Moreover, some boilers may temporarily be stopped to improve the efficiency of those which are kept in operation because it is better to have boilers operating at a power level close to their nominal (maximal) one. Unfortunately, bringing a boiler which have been stopped for a long time (hence which is cold) back into operation entails substantial associated costs because the boiler must be heated up to an adequate temperature, which causes energy consumption without corresponding production. It is thus necessary to think twice before deciding to stop or to restart a boiler. This decision problem is therefore a dynamic problem in which one must anticipate future needs which are of course subject to uncertainties.
This problem of stopping and restarting boilers in the presence of fixed start-up costs is also encountered in electric power companies such as EDF in France, and it is known as the "unit commitment problem" in the international literature. In our study, the inacurracies in predictions around an anticipated production plan have been modeled as a Markov chain, and stochastic dynamic programming techniques have been used to solve the power station management problem.
The management of electric power production in France with help of all the available production means (classical thermal units, nuclear power plants, hydroelectric units, etc.) raises a collection of extremely complex problems at time scales ranging from half an hour (not to speak of network stability problems which involves phenomena at the scale of one second) up to several years when considering the schedule of stopping times of nuclear power plants for maintenance and refuelling. The complexity and variety of problems involved cannot be summarized in a few lines, but one can easily suspect the order of magnitude of the corresponding financial issues.
Électricité de France, and its experts in optimization at the Department of Studies and Research, have been always devoting to such problems a large amount of efforts which is proportional to the importance and difficulties of the matter. As far as CAS is concerned, we have been participating throughout the years to this research effort in close cooperation with EDF engineers. Numerous methodological studies have been motivated by these applications and the corresponding results are quickly captured by EDF to improve the computer assisted decision software in this whole area.
The IET (Intelligent Electric Terminal) is an electric convector equipped with a microprocessor: such a device allows not only a local digital regulation but also some dialog with a central computer. This system makes a more sophisticated global management possible, with account for offices being intermittently used, for the time the various parts of a building are really occupied according to a time schedule, for the possibility of storing energy or anticipating needs according to the electric price within 24 hours (night, day, peak hours) or within the week (working days, week-ends, holiday).
During a cooperation of several years with the research center of EDF-Renardières, we have been studying the following issues:
In France, the company ELF manages three refineries whose activity must be planned over a three month horizon to produce a large variety of petroleum products. This production planning goes with the raw product supplies planning bought on the world market. One can easily imagine the impact of uncertainties affecting both the prices of raw products and those of finished products which are put on the market, and their influence on the market demand.
The planning at the ELF central headquarters must then be polished and adapted in each of the three refineries. Roughly speaking, a refinery can be considered as a network of storages connected by treatment plants which consumes several utilities (steam, electricity, etc.) in addition to the raw or semifinished products. The utilities are produced in the refinery itself or bought from outside.
As one can realize it, the whole system of ELF is a large hierarchical system made of interconnected subsystems which have their own planning horizons ranging from one day to several months, affected by various random factors, and involving huge amounts of money. As for the electric power production of EDF, this system can be considered as a really complex system for which a whole hierarchy of computer-aided decision tools would be very useful. A first attempt in this direction has been made some time ago during a cooperation between ELF France headquarters and CAS; the matter would certainly deserve more substantial efforts.
When a spatial vehicle is put in orbit, the weight of the fuel which is consumed must be subtracted from the weight which is finally placed in orbit. Therefore, one must choose the trajectory which minimizes the fuel consumption (or maximizes the weight placed in orbit). This optimal control problem, which is a priori classical, is in fact rather difficult to solve numerically because of the complexity of the model equations, of the presence of numerous constraints, of the existence of several flight phases with model changes occurring in between (for example, when the first stage of the rocket must be dropped, and possibly recovered), etc. This has required that we set up a so-called finite element method to reach a well mastered discrete formulation of the problem.
Another aspect of the problem pertains to the risk of incident during the ascent phase, which, for a inhabited flight, requires a maneuver to return to earth in a safe way. The chances of successful recovery depend on the ascent trajectory which was followed prior to the incident, and the best choice of a trajectory from this point of view is not necessarily the same as that dictated by the previous weight-in-orbit optimization problem. The trade-off between these two conflicting objectives has been formulated as the maximization of a cost function (the weight placed in orbit) subject to a probabilistic constraint (the probability of recovering the crew successfully must exceed a given threshold). Practically, one must set up an efficient algorithm to solve this problem in order to scan a range of values of the risk threshold and to find the most reasonable level at which it must finally be fixed.
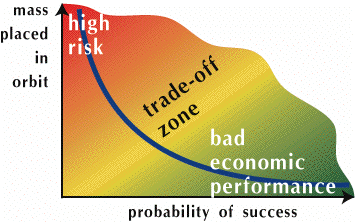
This issue led us to develop an algorithmic research about solving optimization problems with constraints in probability.
The problem consists in defining a policy for issuing orders of nuclear fuel supplies (provided by dedicated plants) in order to refill nuclear power plants during their scheduled stop times. The uncertainties affect the upstream process (technical problems or strikes in the supply plants) as well the downstream process (electricity demand affected by various causes, and power plants failures introducing unexpected stops and thus reducing fuel consumption with respect to schedule). Moreover, orders are only supplied with delays (which can possibly be reduced in case of emergency by paying more). The original feature of uncertainty handling in this study has been the following:
The study has been limited to producing a simulator for performance evaluation and comparison purposes of various management policies, but the simulation itself involves a hidden stochastic optimization problem since one must maximizes (with respect to some of the unknown factors or scenarios) the mathematical expectation (with respect to the probability law of other uncertain factors). An original Monte-Carlo method has been set up to refine the mathematical expectation estimation as the critical (less favorable) scenarios were identified (the Monte-Carlo samples were progressively concentrated on the most critical situations to avoid useless computations).
![]() Back to the list of contents (without frames)
Back to the list of contents (without frames)
|
|
|