Exploiter des modèles mathématiques pour simuler, évaluer, diagnostiquer et gérer de façon optimale des systèmes complexes (voir les applications).
pour estimer les grandeurs non mesurées, utiliser la redondance éventuelle des mesures pour éliminer les erreurs de mesure, détecter les états anormaux, localiser les pannes, etc.
![]() retour au
sommaire sans cadres-frames
retour au
sommaire sans cadres-frames
L'utilisation de méthodes par éléments finis pour la discrétisation
est l'un de nos axes de recherche actuels.
Pour les équations différentielles, l'idée générale est
La qualité de l'approximation obtenue dépend donc surtout de la famille d'éléments finis retenue et de son adaptation au problème considéré. En cette matière, la particularité de certaines équations différentielles (en Mécanique par exemple) suggère des choix individualisés pour chaque type de variable.
Pour les problèmes de commande optimale en temps continu, l'idée générale est similaire, mais on cherche à respecter la même démarche pour toutes les variables du problème, y compris les variables duales (états adjoints, multiplicateurs des contraintes, etc.) et pour toutes les équations ou contraintes apparaissant dans la formulation du problème ; enfin, les fonctions tests des équations primales coïncident en général avec les éléments finis des variables duales et réciproquement. Avec cette démarche, on arrive à réconcilier deux points de vue généralement inconciliables lorsqu'on utilise d'autres méthodes de discrétisation :
L'un des objectifs de ce projet et de parvenir à terme à une "boîte à outils" spécialisée au sein de l'environnement Scilab (graticiel distribué par l'INRIA).
![]() retour au
sommaire sans cadres-frames
retour au
sommaire sans cadres-frames
Il s'agit de surmonter les difficultés dues à la taille énorme des problèmes à résoudre en exploitant la structure des grands systèmes qui n'est généralement pas monolithique.
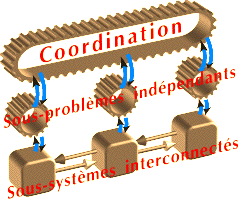
C'est l'autre façon de surmonter la difficulté de la grande dimension ; elle consiste à représenter plusieurs variables par une seule, dans la mesure où, par exemple, ces variables ont un comportement dynamique homogène. En ce sens, l'agrégation est une idée complémentaire de la décomposition car l'homogénéité a plus de chances d'être effective à l'intérieur d'un sous-problème qu'au niveau du système global. L'agrégation doit s'accompagner de désagrégation qui permet d'obtenir une solution qui, au moins, vérifie toutes les contraintes du problème.
La plupart des applications traitées font intervenir des phénomènes aléatoires (pannes, météorologie, consommations...), ce qui nécessite une formulation adaptée.
Des techniques de réduction de variance de l'estimateur ainsi construit ont pu être mises au point dans le cas de probabilités "étagées" (par exemple, dans le cas de panne de divers matériels, la probabilité d'une panne individuelle étant faible, disons d'ordre epsilon, les situations sans panne sont de probabilité proche de un, les situations avec une seule panne sont de probabilité d'ordre epsilon, celles avec deux pannes sont d'ordre epsilon au carré, etc.).
Ces idées ont été combinées avec les techniques de décomposition/coordination afin de résoudre des problèmes d'optimisation stochastique statique de grande taille.
Une technique par chroniques arborescentes a été conçue pour permettre d'étendre les techniques de décomposition/coordination au cadre de l'optimisation dynamique stochastique, au moins pour certains problèmes pour lesquels un "principe de séparation" est vérifié (ce qui recouvre déjà beaucoup d'applications pratiques). L'idée sommaire est de discrétiser l'espace de probabilités (en scénarios ou chroniques) tout en préservant, dans la formulation discrète, les notions essentielles de structures d'information qui permettent d'exprimer par exemple la causalité des stratégies de commande (le fait que les décisions présentes ne dépendent pas d'observations futures).
En plus de vingt cinq années d'existence du projet, on peut classer les principales applications industrielles en trois grandes catégories, mais certaines applications relèvent en fait de deux, voire des trois, catégories.
Il existe en France plusieurs réseaux de distribution d'eau potable d'envergure régionale (constitués progressivement à partir de l'interconnexion de réseaux locaux). Ces réseaux tendent aujourd'hui à être pilotés à partir d'un centre de télécontrôle unique où sont centralisées toutes les mesures disponibles par un réseau de télétransmission, et d'où partent toutes les actions principales de pilotage émanant des décisions d'un opérateur humain seulement secondé par quelques automatismes locaux. Le résultat est que l'opérateur doit faire face à une grande complexité car il devient le cerveau et le centre d'un système tentaculaire permis par la "télé-technologie" moderne.
Le but des études a été de concevoir des outils d'aide à la décision pour cet opérateur humain. Le problème peut être formulé comme un problème de commande optimale classique. Mais, en dehors de son caractère aléatoire évident (les consommations sont prévisibles, mais avec une certaine imprécision), le problème est d'une grande complexité car le système dynamique (le réseau composé de réservoirs, de canalisations, d'organes de pilotage -- vannes, pompes --, d'usines de production d'eau potable, etc.) donne lieu à un modèle mathématique non linéaire et implicite, très lourd à manipuler en optimisation dynamique. La fonction coût représente la facture d'électricité (dont le prix varie par tranches tarifaires au cours des 24 heures, avec malheureusement des pointes coïncidant avec les pointes de consommation d'eau) ainsi que le coût marginal de traitement de l'eau (qui varie géographiquement en fonction de l'origine de la ressource). C'est donc à un vaste problème d'allocation spatio-temporelle de la production qu'il faut faire face (en présence de contraintes d'exploitation diverses).
Grâce à une habile combinaison de techniques de décomposition/coordination et d'agrégation, un problème impliquant une vingtaine de variables d'état (réservoirs) a pu être résolu de façon satisfaisante dans des temps de calcul, sur station de travail standard, tout-à-fait compatibles avec une exploitation quotidienne.
Au delà des économies non négligeables que l'utilisation quotidienne de tels logiciels peut entraîner sur les coûts d'exploitation, le développement rationnel à long terme des réseaux (choix des investissements dans la construction de nouveaux réservoirs et canalisations, négociations des contrats avec fournisseurs et clients, etc.) que permettent ces mêmes logiciels est générateur d'économies encore plus importantes.
À Paris, les réseaux de distribution d'eau courent dans les mêmes galeries que les égouts. Dans ces conditions, une fuite importante due à une casse de tuyau peut rester dissimulée très longtemps, ce qui oblige les exploitants à organiser des rondes périodiques dans les galeries. L'idée est donc d'exploiter toutes les mesures disponibles, ainsi que les modèles mathématiques du réseau (dans leurs aspects qualitatifs et quantitatifs), pour essayer de détecter ces fuites dès qu'elles apparaissent et pour essayer de les localiser le mieux possible.
Le premier aspect du problème est celui de l'observabilité des grandeurs que l'on cherche à surveiller par rapport aux mesures dont on dispose ; il faut répondre à la question : existe-t-il assez de relations mathématiques entre les premières et les dernières pour que la connaissance de celles-ci (éventuellement sur une période de temps) permette de déduire une estimation de celles-là ? C'est un problème algébrique difficile pour des réseaux régis par des lois de type "lois de Khirchoff" et "loi d'Ohm".
Une fois déterminées les grandeurs observables, il s'agit de les estimer numériquement et si possible en temps réel. Ensuite il faut surveiller leur évolution temporelle pour détecter les variations anormales, puis enfin tenter de localiser géographiquement l'origine des incidents.
Un ensemble de programmes a été conçu pour répondre à ces diverses questions. En particulier, au stade de la conception d'un système de mesures ou de son extension, ces programmes peuvent aider au placement de nouveaux capteurs qui "maximiseraient l'observabilité" du système, c'est-à-dire qui amélioreraient la rentabilité de l'investissement.
Des expérimentations conduites sur une partie du réseau parisien ont montré la possibilité de détecter et de localiser avec une bonne précision trois fuites simultanées provoquées artificiellement pendant la nuit par l'ouverture de bouches d'incendies.
Les réseaux de chauffage urbain à eau chaude pressurisée sont constitués de chaufferies brûlant divers carburants (combustibles fossiles, ordures ménagères, etc.), voire utilisant la géothermie comme source de chaleur, et d'un graphe arborescent ou maillés de tuyaux doubles (l'un des tuyaux véhiculant l'eau chaude des chaufferies vers les sous-stations, l'autre ramenant l'eau vers les chaufferies, une fois celle-ci refroidie dans les circuits primaires des échangeurs des sous-stations). Le pilotage de tels réseaux consiste essentiellement à choisir les vitesses des pompes de circulation en sortie des chaufferies, ainsi que les températures de départ des chaufferies. Ces décisions ont deux conséquences :
Accessoirement, il faut optimiser la marche de chaque chaufferie en répartissant la charge globale sur les diverses chaudières opérationnelles en tenant compte de leurs courbes de rendements. On le voit, le problème de pilotage global du réseau est assez complexe, et les enjeux économiques sont importants, compte tenu du fait que ces réseaux sont de grands "dévoreurs" d'énergie.
Un certain nombre de logiciels de simulation et d'optimisation
(aide à la décision pour les concepteurs et
opérateurs) ont été réalisés, tant
en ce qui concerne le régime stationnaire ou lentement
variable, qu'en ce qui concerne les régimes transitoires ; ces
derniers surviennent en particulier au moment de négocier la
"pointe du matin", lorsque les besoins du réseau augmentent
brusquement au passage des consignes de nuit aux consignes de jour,
pour les installations de chauffage des locaux comme pour les besoins
industriels. Dans ce dernier cas, la durée non
négligeable de propagation des "fronts chauds" pour des
réseaux parfois longs de quelques dizaines de
kilomètres introduit des retards qui rendent les
phénomènes non intuitifs. On a pu le constater
grâce à l'optimisation dynamique de régimes
transitoires basée sur des modèles en équations
d'évolution aux dérivées partielles
(hyperboliques non linéaires).
Les grands sites pétrochimiques incluent une centrale d'énergie qui fournit aux unités de production chimique du site de la vapeur à différents niveaux de pression ainsi qu'accessoirement de l'électricité (le reste de la consommation électrique du site étant couverte par le réseau EDF). Pour produire ces diverses utilités, on dispose en général de plusieurs chaudières et turbo-alternateurs, ces derniers permettant le passage de la vapeur du niveau de pression le plus élevé vers les autres niveaux requis en récupérant l'énergie pour une production interne d'électricité. Les surproductions éventuelles de vapeur doivent être "mises au toit", c'est-à-dire déchargées dans l'atmosphère, car elles ne sont pas stockables.
Les données économiques relatives au problème du pilotage d'une telle centrale d'énergie sont assez complexes : rendements des chaudières et des turbo-alternateurs en fonction de leur point de fonctionnement, coût des combustibles, contrats avec EDF, etc. Par ailleurs, certaines chaudières peuvent momentanément être arrêtées pour favoriser celles qui restent en fonctionnement, car il est préférable, du point de vue du rendement, d'avoir des chaudières fonctionnant près de leur régime nominal (puissance maximale). Malheureusement, la remise en route d'une chaudière arrêtée depuis longtemps, donc refroidie, entraîne des coûts annexes importants par nécessité d'une remise en température entraînant une consommation de combustible de plusieurs heures sans contrepartie en production. Il faut donc y regarder à deux fois avant de décider l'arrêt ou le redémarrage d'une chaudière. Le problème devient alors un problème de décision dynamique nécessitant une anticipation des besoins futurs, besoins évidemment sujets à des aléas.
Ce problème de gestion des démarrages-arrêts en présence de coûts fixes de démarrage (les coûts de remise en température) se pose également aux compagnies productrices d'électricité comme EDF en France, et il est connu sous le nom de "unit commitment problem" dans la littérature internationale. Dans notre étude, les erreurs de prévisions autour d'un planning des besoins de production ont été modélisées sous la forme d'une chaîne de Markov, et des techniques de programmation dynamique stochastique ont été utilisées pour résoudre le problème d'optimisation du pilotage de la centrale d'énergie.
La gestion de la production d'électricité en France avec l'ensemble des moyens disponibles (thermiques classiques et nucléaires, hydro-électriques, etc.) soulève un ensemble de problèmes extrêmement complexes à des échelles de temps allant de la demie heure (sans parler des problèmes de stabilité du réseau qui mettent en jeu des phénomènes de l'ordre de la seconde) à plusieurs années en ce qui concerne le placement des arrêts des centrales nucléaires pour entretien/rechargement. La complexité et la diversité de ces problèmes ne peuvent pas être résumés en quelques lignes, mais on se doute de l'importance des enjeux financiers afférents.
Électricité de France, et ses spécialistes en optimisation des Études et Recherches, y consacrent depuis longtemps des efforts à la mesure de ces difficultés et de ces enjeux. Pour ce qui le concerne, le CAS participe depuis plusieurs années en étroite collaboration avec les ingénieurs d'EDF à cet effort de recherche. De nombreux travaux méthodologiques ont été motivés par ces applications et les résultats de ces travaux sont rapidement utilisés par EDF pour améliorer les logiciels d'aide à la décision dans tout ce secteur.
Le TEI (terminal électrique intelligent) est un convecteur électrique équipé d'un microprocesseur : la présence de celui-ci, en dehors de son utilisation comme régulateur local du convecteur, permet le dialogue avec un ordinateur central. Ce système permet alors un pilotage global plus fin, tenant compte, dans les locaux à usage intermittent (bureaux), de l'occupation effective des diverses parties selon les plages horaires, des échanges de chaleur entre ces parties, des possibilités d'accumulation éventuelle de cette chaleur ou de phénomènes d'anticipation pour jouer avec les variations tarifaires de l'électricité avec l'heure de la journée ou avec les jours de la semaine (dimanche, jours fériés). Lors d'une collaboration de plusieurs années avec EDF-Renardières, les études ont porté sur les aspects suivants :
ELF possède en France trois raffineries dont il faut planifier l'activité sur un horizon de trois mois en matière de production de produits pétroliers d'une grande diversité. Cette planification de la production s'accompagne d'une planification des approvisionnements en produits bruts qu'il faut acheter sur le marché mondial. On se doute de l'importance des facteurs aléatoires jouant aussi bien sur le cours des produits bruts que sur celui des produits mis à la vente et sur la demande dans ce domaine.
Cette planification au niveau du siège doit ensuite être affinée et adaptée au niveau des trois raffineries. Une raffinerie est schématiquement un réseau de stocks reliés par des unités de traitement consommant elles-mêmes, en dehors des produits d'entrée, un certain nombre d'utilités (vapeur, électricité, etc.) produites sur place ou achetées à l'extérieur.
On le voit, il s'agit au total d'un très grand système hiérarchisé et composé de sous-systèmes interconnectés, travaillant à des horizons allant de la journée à plusieurs mois, sujet à de nombreux facteurs aléatoires, et mettant en jeu des masses d'argent considérables. Comme pour la production d'électricité à EDF, ce système présente donc toutes les caractéristiques d'un système complexe pour lequel une hiérarchie d'outils d'aide à la décision serait très utile. Une première approche a été effectuée dans cette direction il y a quelques années lors d'une collaboration entre le siège de ELF France et le CAS ; le sujet mériterait certainement des efforts plus importants.
Lors de la mise en orbite d'un engin spatial, le poids du carburant consommé vient en déduction de la charge utile finalement placée sur orbite. On doit choisir la trajectoire qui maximise cette charge utile. Ce problème de commande optimale a priori classique s'avère assez difficile à résoudre numériquement en raison de la complexité des équations du modèle, de la présence de contraintes multiples, de l'existence de plusieurs phases de vol avec changements de modèles (par exemple au moment du largage du premier étage éventuellement récupérable), etc. Ceci a nécessité la mise au point de techniques d'éléments finis pour arriver à une formulation discrète bien maîtrisée.
Un autre aspect du problème tient au risque d'incident en phase de montée, ce qui, dans le cas d'un vol habité, nécessite une manoeuvre de retour sur terre. Les chances de récupération de l'équipage dépendent elles-mêmes de la trajectoire de montée choisie (c'est-à-dire des conditions au moment de l'incident), et le meilleur choix de trajectoire de ce point de vue n'est pas nécessairement compatible avec celui de l'optimisation de la charge utile mise en orbite. Ce problème de compromis a été formulé comme un problème de maximisation d'une fonction objectif (la charge utile) sous une contrainte probabiliste (la probabilité de réussite de la manoeuvre de récupération doit dépasser un seuil donné). Il s'agit pratiquement de mettre au point un algorithme de résolution permettant ensuite, en faisant varier le seuil requis de probabilité de récupération réussie, de mieux cerner le niveau de compromis le plus raisonnable.
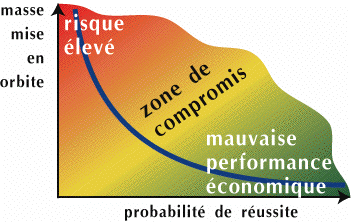
Cette problématique nous a conduits à développer une recherche algorithmique sur les problèmes avec contraintes en probabilité.
Le problème consiste à définir une politique de lancement de commandes d'approvisionnements en combustible nucléaire (fournis par des usines spécialisées) pour recharger les tranches de centrales nucléaires lors de leurs arrêts-rechargement programmés. Les aléas portent aussi bien sur l'amont (aléas techniques et grèves affectant les usines de fabrication) que sur l'aval (aléas divers -- demande d'électricité, pannes -- affectant la marche des tranches nucléaires et donc l'épuisement plus ou moins rapide du combustible). De plus, les commandes ne produisent leurs effets qu'avec retard (délai de livraison, délai qui peut exceptionnellement être réduit au prix de surcoûts). L'originalité de cette étude tient dans le fait que tous les aléas n'ont pas été traités de la même façon :
L'étude s'est limitée à construire un simulateur permettant d'évaluer et de comparer plusieurs stratégies de gestion, mais la simulation elle-même est un problème d'optimisation stochastique caché puisqu'il faut maximiser (par rapport à certains aléas ou scénarios) une espérance mathématique (par rapport à la loi de probabilité des autres aléas). Une méthode de Monte-Carlo originale a été mise au point pour affiner l'estimation de l'espérance mathématique au fur et à mesure que les scénarios les plus défavorables étaient identifiés (les tirages de la méthode de Monte-Carlo se concentrant progressivement sur les scénarios critiques afin d'éviter les calculs inutiles).
![]() retour au
sommaire sans cadres-frames
retour au
sommaire sans cadres-frames
|
|
|