Suiv.: 4 Tests conversationnels Sup.: 3 Introduction Préc.: 3 Introduction Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 4 Tests conversationnels
Sup.: 3 Introduction
Préc.: 3 Introduction
Table des matières
L'exemple suivant est simple et nous servira à montrer comment le résoudre par MODULEF en précisant les notations utilisées.
On commence par donner la formulation du problème, ensuite on indique la formulation variationnelle associée. L'approximation par éléments finis et son implémentation sont alors présentées, en indiquant les différentes étapes à enchainer. Pour ce faire, on considère le problème de Dirichlet décrit ci-dessous:
Le problème s'écrit:
avec
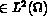 , et
, et
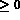 , i.e.,
, i.e.,
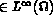 , où
, où 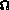 est un sous-ensemble ouvert régulier de
est un sous-ensemble ouvert régulier de 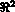 de frontière
de frontière
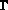 régulière.
régulière.
La formulation variationnelle (ou faible) de ce problème est:
Trouver 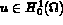 , l'espace des fonctions admissibles, tel que
, l'espace des fonctions admissibles, tel que
pour tout 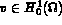 .
.
Cette formulation variationnelle est le point de départ de la méthode des éléments finis.
Remarque: L'analyse détaillée des solutions des problèmes (3.1) et (3.2) n'est pas l'objet de ce papier aussi le lecteur pourra consulter par exemple "The Finite Element Method for Elliptic Problems" par P. G. Ciarlet (1978)).
A première vue, ce problème ne peut pas être résolu par MODULEF. Néanmoins, une analyse plus fine montre que l'on peut le considérer comme un problème de type thermique.
La méthode des éléments finis consiste à chercher une solution approchée dans un sous-espace de
dimension finie.
Pour résoudre le problème (3.2), on doit le poser dans cet espace discret, l'équation
(3.2) devient:
Trouver la solution approchée 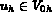 telle que
telle que
pour tout 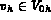 ,
avec comme espace discret
,
avec comme espace discret 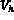 et
et 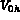 définis par:
définis par:
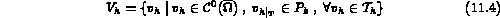
et
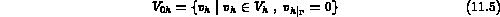
où
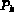
Avant de revenir sur l'équation (3.3), nous introduisons les notations suivantes:
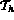 le maillage du domaine
le maillage du domaine  , avec T un élément de
, avec T un élément de
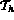 , tel que
, tel que
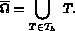
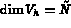 où
où 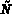 est le nombre total de degrés de liberté.
est le nombre total de degrés de liberté.
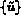 est la valeur de la fonction.
est la valeur de la fonction.
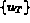 est la valeur de la fonction aux degrés de liberté de l'élément T.
est la valeur de la fonction aux degrés de liberté de l'élément T.
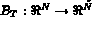
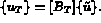
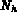 est l'ensemble des degrés de liberté sur la frontière.
est l'ensemble des degrés de liberté sur la frontière.
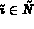 (ou
(ou 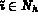 ) indique que le degré de liberté global
) indique que le degré de liberté global
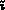 est interne (ou sur la frontière).
est interne (ou sur la frontière).
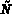 fonctions de base,
fonctions de base, 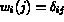 , base de l'espace
, base de l'espace 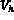 ,
,
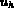 s'écrit
s'écrit
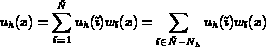
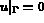 .
. 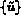 s'écrit comme
s'écrit comme
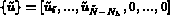
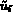 sont les composantes de
sont les composantes de 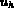 sur la base
sur la base 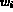 , si on suppose
que les degrés frontières sont numérotés en dernier.
, si on suppose
que les degrés frontières sont numérotés en dernier.
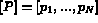
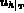 s'exprime comme:
s'exprime comme:
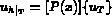
Notant la dérivée de 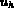 par
par
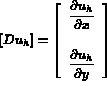
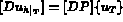
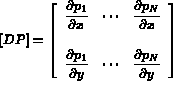
L'équation (3.3) s'exprime alors en fonction de ces quantités par:
Trouver 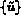 avec
avec
 , pour
, pour 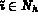 , tel que
, tel que
pour tout 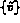 tel que
tel que  ,
, 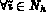 .
.
A ce stade, l'obtention à partir de la formulation (3.3) de la formulation (3.6) est tout à fait générale (indépendante de MODULEF). Il reste maintenant à définir les opérateurs mathématiques utiles et à trouver leur correspondant dans MODULEF.
Rappelons d'abord le problème thermique classique, tel qu'il est
décrit dans
[4] [Guide Modulef - 7], qui est
complètement résolu par MODULEF, et pour lequel la matrice élémentaire de rigidité, la matrice
élémentaire de masse et le second membre élémentaire sont donnés par:
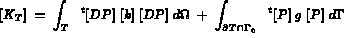

Alors, si on pose:
[k] = [I] : la conductivité thermique ([I] : matrice unité),
g=0 : le coefficient de transfert à travers 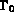 ,
,
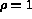 : la densité, et
: la densité, et
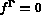 : les forces sur la frontière.
: les forces sur la frontière.
dans le cas classique, on retrouve les matrices et seconds membres élémentaires du problème de Dirichlet que l'on cherche à résoudre, c'est-à-dire:
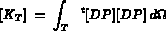
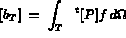
Ainsi l'équation (3.6) de notre problème, identifié comme un problème thermique simplifié, peut être résolue entièrement par MODULEF.
Remarque: La liste et la description des éléments finis pour les problèmes thermiques présents dans le code MODULEF est donnée dans [Guide Modulef - 7].
Avec ces notations, (3.6) devient:
Trouver 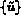 avec
avec  ,
,
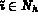 , tel que
, tel que
pour tout 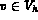 , tel que
, tel que 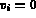 ,
, 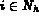 , ceci donne un système linéaire
de matrice définie positive.
, ceci donne un système linéaire
de matrice définie positive.
Soit 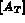 la matrice associée à l'élément T, alors
la matrice associée à l'élément T, alors
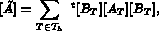
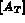 .
.
Il y a deux interprétations possibles pour cet exemple:
si 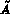 est la matrice du système à résoudre, on peut écrire:
est la matrice du système à résoudre, on peut écrire:
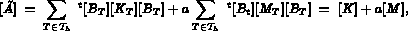
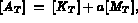
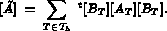
Du point de vue mathématique, ces formules sont identiques. Néanmoins, elles donnent lieu,
du point de vue du calcul sur ordinateur, à deux problèmes différents.
Dans les deux cas, il est nécessaire de calculer les masses élémentaires 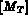 et les
rigidités élémentaires
et les
rigidités élémentaires 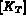 , ensuite soit on:
, ensuite soit on:
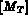 , donnant [M],
, donnant [M],
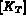 , donnant [K], et
, donnant [K], et
Après avoir assemblé les matrices, l'équation (3.9) devient:
Trouver 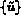 avec
avec  , pour tout
, pour tout 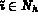 , tel que
, tel que
pour tout 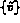 avec
avec 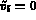 ,
, 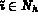 .
.
Comme 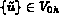 est de la forme:
est de la forme:
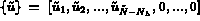
on peut décomposer (momentanément) 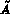 et
et 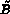 en
en
où 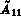 est une
est une 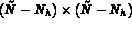 matrice.
matrice.
Avec cette décomposition, en utilisant le fait que 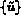 et
et 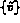 sont dans
sont dans 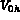 ,
l'équation (3.10) devient:
,
l'équation (3.10) devient:
Ainsi, pour calculer 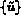 , il faut résoudre (3.12), ou seulement:
, il faut résoudre (3.12), ou seulement:
où 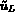 est un vecteur de dimension
est un vecteur de dimension 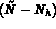 ,
dont les composantes sont les
,
dont les composantes sont les 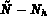 premières composantes de
premières composantes de 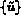 .
.
Remarques:
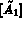 (équation (3.12)), en assemblant les éléments
(équation (3.12)), en assemblant les éléments
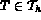 , nécessite de distinguer les éléments
, nécessite de distinguer les éléments 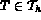 de
de
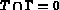 de ceux de
de ceux de 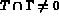 , pour prendre en compte la condition
, pour prendre en compte la condition 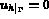 .
.
Il est donc plus simple de calculer en premier 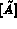 puis
puis 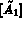 , c'est la
prise en compte des conditions aux limites imposées.
, c'est la
prise en compte des conditions aux limites imposées.
En suivant cette analyse, on a déterminé les différents opérateurs mathématiques et de ce fait, le problème se décompose en les étapes suivantes:
Remarque: Les étapes 1) et 2) dépendent de la formulation variationnelle choisie.
Chaque étape est décomposée en sous-étapes. La décomposition de chaque étape, tout comme le choix
des modules assurant le calcul des opérateurs mathématiques, sont présentés dans la suite de cette
section.
Suivent quelques mots usuellement utilisés par la suite:
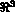 , lignes et points en
, lignes et points en 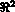 ou
ou 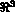 ).
).
Ces attributs servent à traiter par lot des conditions aux limites, des forces ou à définir les lignes (surfaces) courbes.
Sur la figure 3.1, le corps est fixé sur la frontière AF, et chargé le long de la frontière CD. Il comprend deux matériaux, un trou circulaire et un demi-trou.
Il y a donc deux sous-domaines:
et au moins quatre numéros de référence:
Remarque: Les lignes AC et FD n'ont pas de numéros particuliers
car elles ne supportent aucunes
conditions particulières.
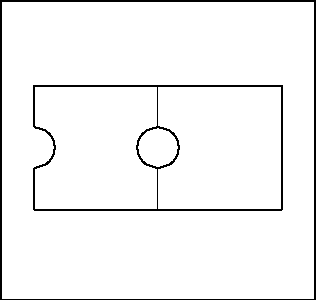
Figure: Domaine encastré et chargé
Sur la figure 3.2 on voit un triangle P2 droit et un triangle P2 courbe. Un élément droit est un élément dont les points sont les sommets. Un élément courbe est un élément dont les points sont les sommets et d'autres points non sommets. Dans le cas du triangle P2, l'élément droit est défini par 3 points alors que le courbe a 6 points, tout deux ayant 6 noeuds.
Les différents opérateurs mathématiques introduits pour décomposer le problème exemple sont, du point de vue pratique, réalisés par un programme de calcul ou module. Ces modules communiquent entre eux via les structures de données (S.D.). Dans cette section, nous donnons le détail de ces correspondances.
Le maillage doit respecter les règles générales des maillages éléments finis.
Si 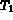 et
et 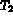 sont éléments de
sont éléments de 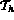 alors:
alors:
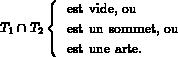
|
|
L'implémentation d'un mailleur n'est pas triviale (cf. par exemple [George-1986]) et de plus, même si les opérateurs nécessaires sont inclus dans le code, la construction du maillage demande un certain temps. Notons qu'un bon maillage est une condition importante pour obtenir de bons résultats numériques.
La technique de génération de maillages de MODULEF est arborescente (ascendante et descendante), le domaine est décomposé en sous-domaines géométriquement plus simples. Ces derniers sont manipulés par des opérateurs simples (symétrie, rotation, translation, etc.) et recollés ensuite de façon à obtenir le maillage final. Dans le cas bidimensionnel, le module APNOPO est à utiliser, on trouvera une description des techniques et des différents modules possibles dans [Guide Modulef - 3].
Le maillage résultat est stocké dans une S.D. NOPO. Cette S.D. contient la description du maillage: les éléments, les noeuds (sommets ou non), les coordonnées des sommets, ..., qui ont été créés.
A ce stade, on n'a pas encore défini l'interpolation (si ce n'est la numérotation des noeuds), c'est l'objet de l'étape suivante.
Exemple:
|
|
Le dessin du maillage construit est obtenu grâce au module
TRNOPO
[4] [Guide Modulef - 6], décrit
plus bas.
Dans cette étape, on prend en compte les fonctions d'interpolation. Ceci se fait via le module COMACO [Guide Modulef - 4]. Deux cas existent:
Les résultats de ce calcul se trouvent dans les deux structures de données MAIL et COOR. La S.D. MAIL contient la description du maillage (noeuds, points, etc.) et celle de l'interpolation (nombre et nom des inconnus variationnelles, mnémoniques, etc.). La S.D. COOR contient les coordonnées des points (sommets ou non).
Note: La S.D. COOR ne contient pas les coordonnées des noeuds en sortie de COMACO. Si on reprend le cas des éléments triangle P2 droit et P2 courbe, dans le premier cas, la S.D. COOR contient les coordonnées des sommets alors que dans le second cas, elle contient celles des sommets et des milieux d'arêtes.
Cette étape a pour but de construire, élément par élément, les matrices et le second membre
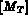 ,
, 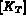 , et
, et 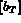 .
Ce calcul nécessite la connaissance des données physiques décrivant les matériaux,
les efforts, etc.
Dans cet exemple, cela correspond à f et a qui apparaissent dans l'équation.
Toutes ces données doivent être connues lors de l'activation du module calculant les tableaux
élémentaires.
.
Ce calcul nécessite la connaissance des données physiques décrivant les matériaux,
les efforts, etc.
Dans cet exemple, cela correspond à f et a qui apparaissent dans l'équation.
Toutes ces données doivent être connues lors de l'activation du module calculant les tableaux
élémentaires.
Il y a deux possibilités:
Dans tous les cas, il est possible de fournir ces valeurs par numéros de sous-domaine et/ou de référence, ce qui minimise le nombre de valeurs à fournir. Les résultats de cette étape consistent en la S.D. TAE qui contient les matrices et les seconds membres associés à tous les éléments du maillage.
Remarques:
D'autres modules correspondent à cette étape pour certains problèmes spécifiques (ex. COTAE pour un problème d'élasticité non linéaire en grandes déformations [97]; BIHAP1, BIHAP2 pour le problème biharmonique [93], etc.).
Ce calcul est décomposé en plusieurs sous-étapes. Le principe général est le même quelque soit le cas, les différences sont liées à la méthode choisie. Le code MODULEF contient un grand nombre de méthodes de résolution des systèmes linéaires, parmi lesquelles on trouve:
Les matrices associées à une discrétisation de type éléments finis sont creuses. Afin de minimiser la place occupée, un stockage approprié est choisi:
Un problème non linéaire pourra souvent être vu comme une suite de problèmes linéaires, chacun de ceux-ci étant traité comme ci-dessous.
Choisir une méthode de résolution pour un système linéaire n'est pas simple et dépend fortement de la nature du problème à résoudre. Pour les systèmes simples, toutes les méthodes donnent de bons résultats. Quand il y a plusieurs systèmes à résoudre, par exemple de manière itérative, il y a des arguments en faveur des deux types de méthodes:
Pour analyser les différentes sous-étapes, on se place dans le cas d'un système linéaire traité par la méthode de Cholesky en mémoire centrale (m.c.).
Cette étape est faite par le module PREPAC [Guide Modulef - 5]. Le résultat est mis dans une S.D. MUA, qui ne contient pas encore la matrice mais uniquement les pointeurs.
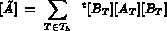
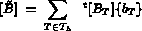
Les résultats de ces calculs constituent la S.D. MUA, contenant la matrice, et la S.D. B, contenant le second membre.
Le but de cette étape, divisée en deux parties, est de traiter ce deuxième cas.
Remarques:
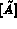 , la matrice
, la matrice 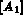 , selon les équations
(3.11) et (3.12).
, selon les équations
(3.11) et (3.12).
Il y a plusieurs techniques pour prendre en compte pratiquement ces conditions aux limites, voir [Guide Modulef - 5]: le module CLIMPC, pour les matrices profils. Conceptuellement, nous distinguons deux classes:
L'idée de base est l'égalité (sur ordinateur) suivante:
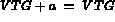
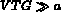 (par exemple:
(par exemple: 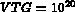 et
et 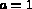 ).
).
En pratique, on part de 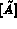 et de
et de 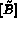 de l'équation (3.11), et on remplace les
coefficients diagonaux de
de l'équation (3.11), et on remplace les
coefficients diagonaux de 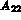 par VTG et les coefficients de
par VTG et les coefficients de 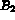 par
par 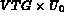 , où
, où
avec

Une variante de cette méthode consiste à remplacer les coefficients diagonaux de 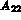 par:
par:
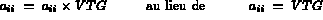
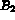 par:
par:

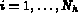 .
.
Avantages et désavantages:
En résumé:
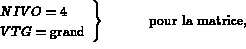
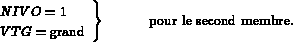
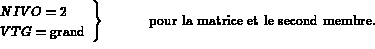
L'idée est d'obtenir l'équation (3.12) à partir de (3.11) effectivement. Notons que dans l'équation (3.12) on a perdu la propriété de symétrie de la matrice. Ceci est important car pour une matrice symétrique, on ne stocke que la moitié des coefficients. Néanmoins, on veut obtenir (3.15), équivalent à (3.12), à partir de l'équation (3.11), où (3.15) est symétrique.
Dans le cas général (d.l. imposés à une valeur de  , nulle ou non (3.14)), si
on prend la décomposition de
, nulle ou non (3.14)), si
on prend la décomposition de 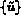 :
:
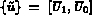


l'équation (3.12) peut être écrite comme:
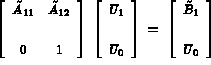
qui est équivalent à:
En pratique, c'est l'équation (3.15) qui est calculée en suivant les notations de [Guide Modulef - 5]:
PROFIL et CLIMPC, avec NIVO = 3 et VTG = 1).
Remarque: Les différentes techniques sont indépendantes du mode de stockage des matrices, et, par suite, s'appliquent dans le cas où d'autres stockages sont utilisées.
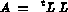
Le résultat est une S.D. MUA qui contient la matrice factorisée.
Le résultat est une S.D. B.
Commentaires:
La solution d'un système linéaire est décomposée en plusieurs étapes dans le but
de simplifier la phase de calcul sur ordinateur. Par exemple:
La visualisation des résultats est un point important. En fait, il est difficile d'analyser un résultat en regardant uniquement le contenu d'une structure B. Afin d'aider à cette analyse, les outils suivants sont disponibles:
Au cours du post-traitement, on peut aussi utiliser les modules de modification des structures NOPO [Guide Modulef - 3] et B. Par exemple, si le problème est symétrique, le calcul peut se faire uniquement sur une partie du domaine. S'il est souhaité de présenter les résultats sur le domaine complet, on peut recoller ensemble la solution calculée et son symétrique et les maillages correspondants.
Par cet exemple, on a illustré comment trouver les modules voulus dans les bibliothèques. Néanmoins, on n'a pas indiqué comment utiliser ces modules. Les exemples suivants vont décrire en détails ce point.