Suiv.: Cas des poutresbarres et Sup.: Les éléments finis élastiques Préc.: 2.4 Cas des plaques Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Cas des poutresbarres et
Sup.: Les éléments finis élastiques
Préc.: 2.4 Cas des plaques
Index
Table des matières
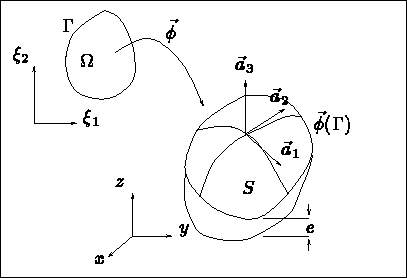
Figure 2.5: La surface moyenne de la coque
Dans le cas où une dimension du domaine est
petite par rapport aux deux autres, si le
matériau est homogène isotrope et si les efforts
appliqués sont suffisamment faibles pour que
l'hypothèse des petites perturbations soit valable,
alors, le modèle tridimensionnel général, par
intégration sur l'épaisseur, donne un modèle bidimensionnel qui approche bien le problème. Dans le cas où la
surface moyenne est quelconque(![]() Par opposition avec le cas des plaques, voir ci-dessus.),
ce modèle est celui des coques. Plus précisément nous prendrons le modèle de coque de Koiter.
Par opposition avec le cas des plaques, voir ci-dessus.),
ce modèle est celui des coques. Plus précisément nous prendrons le modèle de coque de Koiter.
Soit  un ouvert borné de R² de frontière
un ouvert borné de R² de frontière 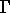 . La surface moyenne
. La surface moyenne 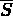 de
la coque est l'image dans R³ de l'ensemble
de
la coque est l'image dans R³ de l'ensemble  par une carte
par une carte 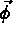 :
:
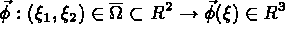
L'épaisseur de la coque est définie par l'application:
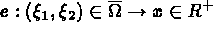
La coque 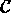 est alors le sous-ensemble fermé de
est alors le sous-ensemble fermé de 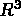 défini par:
défini par:
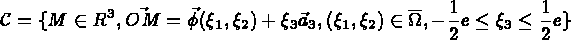
L'expression du tenseur des déformations de la coque se ramène en première approximation à l'évaluation des 2 tenseurs de surface suivant:
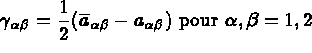
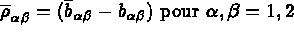
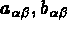 désignent les première et seconde formes fondamentales de la
surface moyenne S avant déformation et
désignent les première et seconde formes fondamentales de la
surface moyenne S avant déformation et 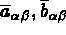 ces
mêmes formes pour la configuration déformée, i.e.
ces
mêmes formes pour la configuration déformée, i.e.
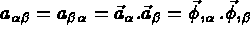
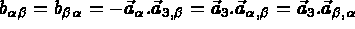
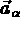 on associe les vecteurs
on associe les vecteurs 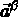 du plan tangent définis par
du plan tangent définis par
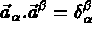
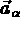 par:
par:
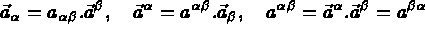
On désigne par 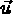 le champ de déplacement des points de la surface S et on pose
le champ de déplacement des points de la surface S et on pose
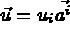 ;
les trois fonctions
;
les trois fonctions 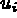 sont les inconnues du problème. On montre alors qu'il est possible d'exprimer les
tenseurs
sont les inconnues du problème. On montre alors qu'il est possible d'exprimer les
tenseurs 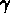 et
et 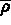 introduits ci-dessus en fonction de
introduits ci-dessus en fonction de 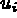 .
.
L'énergie de déformation de la coque associée à un champ de déplacement donné 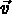 de
la surface moyenne S s'écrit:
de
la surface moyenne S s'écrit:
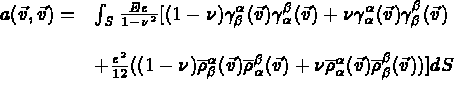
avec E le module de Young et  le coefficient de Poisson et
le coefficient de Poisson et
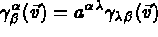
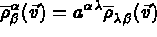
Le travail des forces extérieures s'écrit:
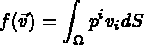
Trouver 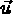 dans l'espace
dans l'espace
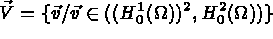
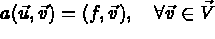
avec :
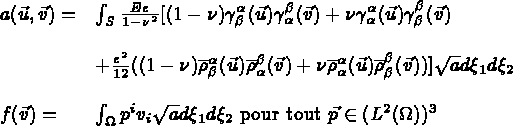
Ce problème peut être approché par des méthodes d'éléments finis conformes à l'aide du triangle d'Argyris de degré 5 (élément TRIA ARGC). L'implémentation est détaillée dans [Bernadou].