Suiv.: 2.5 Cas des coques Sup.: Les éléments finis élastiques Préc.: Cas axisymétrique Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 2.5 Cas des coques
Sup.: Les éléments finis élastiques
Préc.: Cas axisymétrique
Index
Table des matières
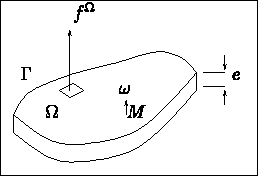
Figure: Présentation du problème
Dans le cas où une dimension du domaine est
petite par rapport aux 2 autres, si le
matériau est homogène isotrope et si les efforts
appliqués sont normaux au plan définissant la
petite dimension et suffisamment faibles pour que
l'hypothèse des petites perturbations soit valide,
alors, le modèle tridimensionnel général, par
intégration sur l'épaisseur, donne un modèle bidimensionnel qui approche bien le problème. Dans le cas où la
surface moyenne est plane(![]() Dans le cas inverse, on trouve les modèles de coques, voir plus bas.),
ce modèle est celui des plaques dans lequel on calcule w la flèche de la plaque
qui satisfait, en suivant le modèle de Kirchhoff, à l'E.D.P. suivante:
Dans le cas inverse, on trouve les modèles de coques, voir plus bas.),
ce modèle est celui des plaques dans lequel on calcule w la flèche de la plaque
qui satisfait, en suivant le modèle de Kirchhoff, à l'E.D.P. suivante:
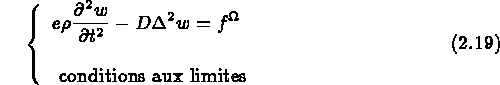
avec
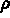 la densité volumique du matériau,
la densité volumique du matériau,
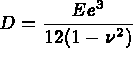 ,
,
 le coefficient de Poisson
le coefficient de Poisson
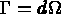 ):
):
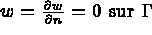 ,
,
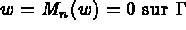 où
où 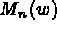 est le moment de flexion (que
l'on trouvera en utilisant la formule de Green),
est le moment de flexion (que
l'on trouvera en utilisant la formule de Green),
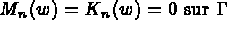 où
où
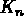 est l'effort tranchant effectif (ces quantités apparaîtront par application de la formule de Green).
est l'effort tranchant effectif (ces quantités apparaîtront par application de la formule de Green).
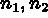 ) est la normale unitaire dirigée vers l'extérieur,
) est la normale unitaire dirigée vers l'extérieur,
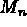 désigne le moment de flexion et
désigne le moment de flexion et 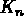 désigne l'effort tranchant effectif définis par:
désigne l'effort tranchant effectif définis par:
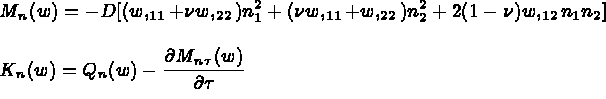
où l'on note 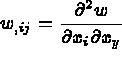 . Par ailleurs,
. Par ailleurs,
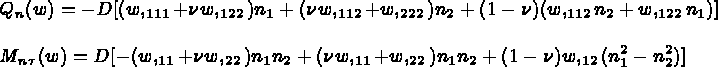
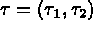 la tangente unitaire déduite de la normale par rotation de
la tangente unitaire déduite de la normale par rotation de 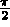 .
.
Dans le cas transitoire, on ajoute la condition initiale portant sur w et sur 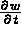 , c'est-à-dire les deux valeurs au temps initial.
, c'est-à-dire les deux valeurs au temps initial.
Formulation en déplacement
Dans le cas d'une plaque encastrée (cas ci-dessus), une formulation possible est la suivante:
Trouver, à chaque instant t, la flèche w dans l'espace
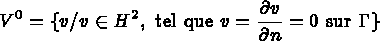
solution de :
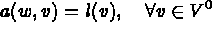
ou après discrétisation
trouver, à chaque instant t, la flèche 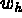 dans l'espace
dans l'espace
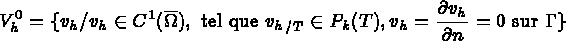
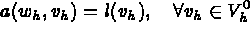
avec :
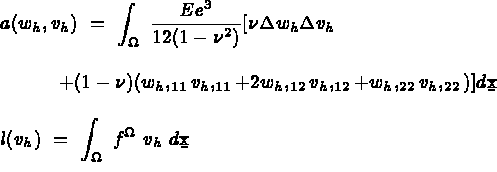
Autres formulations
L'idée est d'introduire une deuxième inconnue u liée à w par des relations différentes (ce qui donne différentes méthodes) et à découper le problème sous la forme :
Trouver, à chaque instant t, le couple (u,w) dans l'espace 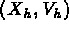 solution de
solution de
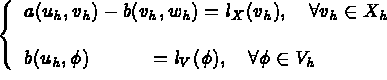
avec des choix différents pour les espaces 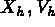 et les opérateurs
et les opérateurs
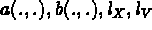 .
.

Par cette méthode on obtient une solution 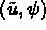 telle que
telle que 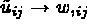 et
et
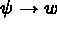 .
.
Pour la valeur k=0 , l'expression b(.,.) se simplifie en
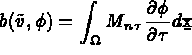
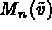 aux interfaces.
aux interfaces.
On introduit l'espace:

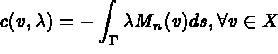
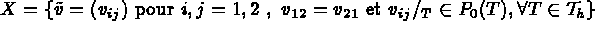
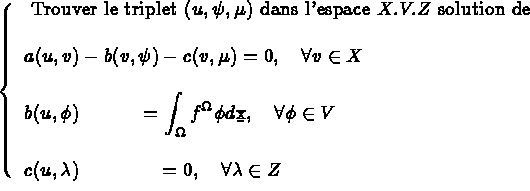
On résout ce système (c'est l'exemple de l'élément TRIA HHJ1).
Pour chaque entier m>0,r>2,s>0 on définit:
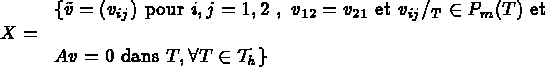
avec
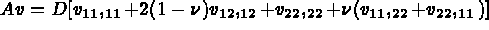
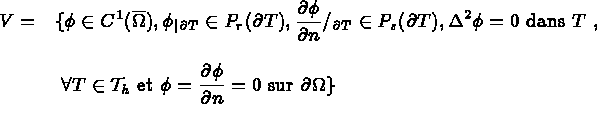
et le choix
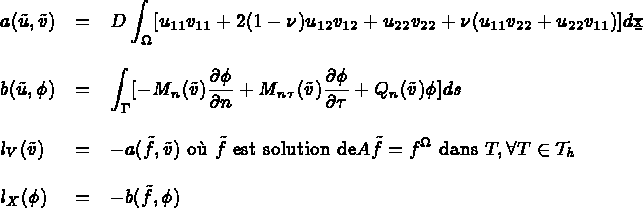
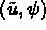 qui pour le choix
r=3,s=m=1, c'est-à-dire l'élément TRIA H31D,
est telle que
qui pour le choix
r=3,s=m=1, c'est-à-dire l'élément TRIA H31D,
est telle que
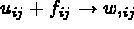 dans T et
dans T et
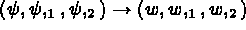 aux interfaces entre éléments.
aux interfaces entre éléments.