Suiv.: 7.7 Tris et dichotomies Sup.: 7 Programmes internes Préc.: 7.5 Conversions Index Table des matières

7.6 Manipulations de matrices et vecteurs

      SUBROUTINE NRMVCT(V1, V)
      REAL V1(3), V(3)

Normalisation du  vecteur V1 :

      SUBROUTINE PRDVCT(V1, V2, V)
      REAL V1(3), V2(3), V(3)

Produit vectoriel  : V=V1*V2

       REAL FUNCTION PRDSCL(V1, V2)
       REAL V1(3), V2(3)

Produit scalaire  : PRDSCL=V1.V2

      REAL FUNCTION PRDMXT(V1, V2, V3) 
      REAL V1(3), V2(3), V3(3)
      EXTERNAL PRDSCL
      REAL PRDSCL

Produit mixte  : PRDMXT=V1.(V2*V3)

      SUBROUTINE  NORMAL(CC)
      REAL CC(4)

Convertit les  CC(1:4), en coordonnées homogènes, en coordonnées normales. (c'est-à-dire telles que CC(4) = 1.).

L'appel des sous-programmes permettant les transformations dans l'espace tridimensionnel déclenche un processus de calcul d'une matrice, correspondant à l'application linéaire associée à la transformation.

D'autres sous-programmes permettent le calcul du clipping (voir masques et fenêtres). Généralement l'utilisateur n'a pas à s'occuper de ces sous-programmes. Cependant pour certains calculs (pas forcémment graphiques !) il est possible d'utiliser avantageusement ces procédures d'un intérêt pratique.

Il est cependant nécessaire de préciser certaines notions.

Les procédures internes de FORTRAN 3D manipulent une matrice 4*4 de type réel, que nous appelerons MAT(4, 4) par la suite, telle qu'une sous matrice 3*3 extraite de celle-ci représente la rotation et un vecteur placé en dernière colonne représente la translation. Le coin inférieur droit de la matrice contient le nombre 1. et les trois premiers éléments de la dernière lignes sont nuls :

 
    MAT(1:3, 1:3)   ---> Rotation                |  R  R  R  T  |
    MAT(1:3,  4 )   ---> Translation             |  R  R  R  T  |
                                                 |  R  R  R  T  |
    MAT(4, 1:4)     ---> Affine                  |  0  0  0  1. |

Avant toute opération il faut initialiser MAT à la matrice unité. L'appel séquentiel des procédures de transformation multiplie la matrice en cours par la matrice correspondant à la transformation demandée. A la fin des opérations la matrice contient le résultat de toutes les opérations effectuées.

      SUBROUTINE MATUNI(MAT)
      REAL MAT(4, 4)

Renvoie dans MAT une  matrice unité. L'appel de cette procédure est obligatoire avant l'utilisation des sous-programmes qui suivent.

      SUBROUTINE LDMAT(MAT)
      REAL MAT(4, 4)

Renvoie dans MAT la  matrice du niveau de pile courant. Cette procédure peut remplacer la précédante si on désire effectuer des transformations relatives au niveau actuel des opérations en cours, au lieu de partir de l'identitée.

      SUBROUTINE PRDMAT(MAT1, MAT)
      REAL MAT1, MAT

Renvoie dans MAT le  produit matriciel : MAT = MAT1 * MAT

      SUBROUTINE TRSFO1(P, MAT)
      REAL P(4), MAT(4, 4)

Renvoie dans le  vecteur P le produit : P = P*MAT . Après transformation P est en coordonnées homogènes.

      SUBROUTINE INVMAT(MAT, MAT1)
      REAL MAT(4, 4), MAT1(4, 4)

Renvoie dans MAT1 l'inverse de  MAT calculée par la méthode de Gauss-Jordan (pivot maximum).

      SUBROUTINE TRSLL(A, B, C, MAT)
      REAL A, B, C, MAT(4, 4)

La translation est  définie par: X = X + A , Y = Y + B et Z = Z + C . Calcule une matrice de translation M1, puis renvoie dans MAT le produit matriciel : MAT = M1 * MAT

      SUBROUTINE ROTT(I, BETA, MAT)
      INTEGER I
      REAL BETA, MAT(4, 4)

Calcule une matrice de  rotation M1 d'un angle BETA autour d'un axe défini par la valeur de I : I=1 axe OX, I=2 axe OY ou I=3 axe OZ

puis renvoie dans MAT le produit matriciel : MAT = M1 * MAT

      SUBROUTINE SCALEE(A, B, C, MAT)
      REAL A, B, C, MAT(4, 4)

Mise à l'échelle : X = A * X , Y = B * Y et Z = C * Z

Calcule une matrice de mise à l'échelle M1, puis renvoie dans MAT le produit matriciel : MAT = M1 * MAT

      SUBROUTINE SHEARR(A, B, C, MAT)
      REAL A, B, C, MAT(4, 4)

Définit une  matrice de cisaillement. C'est-à-dire la transformation suivante : 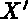= X + B*Y + C*Z , 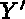= A*X + Y + C*Z et 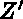= A*X + B*Y + Z

Puis renvoie dans MAT le produit matriciel : MAT = M1 * MAT

      SUBROUTINE REPERR(XO, YO, ZO, XR, YR, ZR, IVERTI, MAT)
      REAL XO, YO, ZO, XR, YR, ZR, MAT(4, 4)
      INTEGER IVERTI

(XO, YO, ZO) est la  position de l'observateur dans le repère de l'objet.

(XR, YR, ZR) représente les coordonnées du point regardé dans le même repère.

IVERTI est la verticale du repère initial

IVERTI = 1 OX verticale

IVERTI = 2 OY verticale

IVERTI = 3 OZ verticale

On peut alors associer à l'observateur un repère local tel qu'il soit placé à l'origine de celui-ci, regardant dans la direction de Z négatifs (position normalisée).

Ce sous-programme calcule la matrice de cette transformation, M1, puis renvoie dans MAT le produit matriciel : MAT = M1 * MAT

Voir aussi le sous-programme NRMLST.

      SUBROUTINE ROTAXX(PX, PY, PZ, VX, VY, VZ, THETA, MAT)
      REAL PX, PY, PZ, VX, VY, VZ, THETA, MAT(4, 4)

Calcule une matrice de  rotation d'un angle THETA radians autour de l'axe défini par le vecteur d'origine (PX, PY, PZ) et de composantes (VX, VY, VZ), puis renvoie dans MAT le produit matriciel : MAT = M1 * MAT

Correspond au sous-programme ROTAXE.

      SUBROUTINE SYMTRR(I, J, MAT)
      REAL MAT(4, 4)
      INTEGER I, J

Voir le  sous-programme SYMTRI.

I=1 symétrie par rapport à l'origine

I=2 symétrie par rapport au plan : J=1 xoy , J=2 yoz , J=3 zox

I=3 symétrie par rapport à l'axe : J=1 ox , J=2 oy , J=3 oz

Calcule une matrice M1 de symétrie, puis renvoie dans MAT le produit matriciel : MAT = M1 * MAT

      SUBROUTINE POS3DD(P1, P2, P3, Q1, Q2, Q3, MAT)
      REAL P1(3), P2(3), P3(3), Q1(3), Q2(3), Q3(3), MAT(4, 4)

Crée MAT matrice qui  positionne l'objet défini par P1, P2, P3 sur Q1, Q2, Q3. Voir le sous-programme POS3D.

Calcule une matrice M1 de transformation, puis renvoie dans MAT le produit matriciel: MAT = M1 * MAT