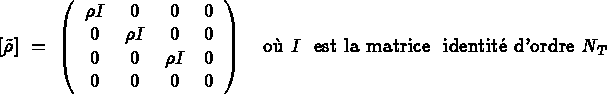Suiv.: Le système global Sup.: Le problème de la piézoélectricité Préc.: 1.2 Formulation variationnelle Index Table des matières

Généralités sur le traitement du problème

Pour ce paragraphe, le lecteur se reportera avantageusement au cas de l'élasticité tridimensionnelle. Le problème se trouve simplement généralisé au cas piézoélectrique par l'ajout d'une inconnue variationnelle potentiel électrique , et on aura, avec les mêmes notations que pour l'élasticité( REMARQUE: Le choix des indices pour les termes de cisaillement dans la représentation vectorielle du tenseur des déformations correspond à la norme en vigueur chez les céramistes, et c'est le seul qui assure la compatibilité des constantes (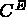,...) fournies par ceux-ci.):

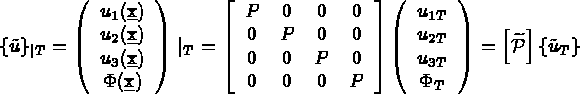
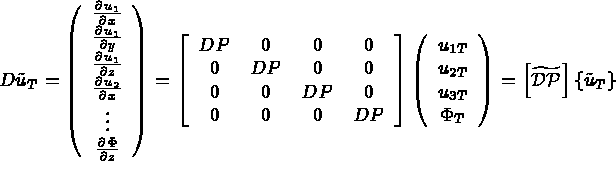
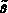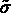Les tenseurs (notation en élasticité) et s'écrivent:

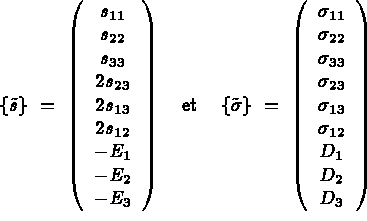
Et la loi de comportement piézoélectrique est donnée par 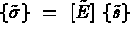avec:

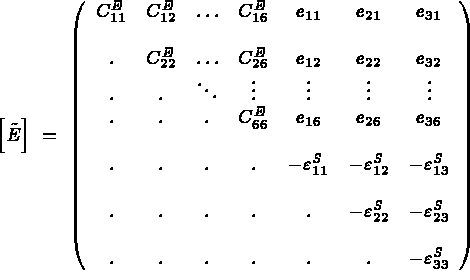
Ainsi généralisé, le calcul des matrices élémentaires se fait de façon identique au cas élastique. La seule différence se situe au niveau de la matrice de masse pour laquelle le coefficient est à remplacer par la matrice donnée ci-dessous, pour tenir compte du fait qu'il n'existe pas de terme inertiel sur les potentiels électriques: