




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: segm2por
Sup.: 9 Fiches techniques
Préc.: pent3r2c
Index
Table des matières
Bibliothèque '
Elasticité' -
Elément fini:
TRIA P2P1
A. Kaiss, INRIA
DESCRIPTION DE L'ELEMENT
- Dimension de l'espace : 2, élément bidimensionnel incompressible
- Inconnues :
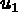 et
et 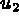 , les déplacements (ou vitesses) suivant x et y et la pression
, les déplacements (ou vitesses) suivant x et y et la pression
- Formulation variationnelle : mixte
- Numéro de code : 200 026
- numéro de code géométrique : 3 (triangle)
- Interpolation : P1-iso-P2-P1
- Nombre de points : 3
- Nombre de types de points : 1
- Les points sont définis par leurs seules coordonnées : NCACAR=0
- Nombre de noeuds : 6
- Nombre de types de noeuds : 2
- Type de noeud 1 : les sommets, 3 d.l. par noeud, 'VN' pour
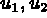 et 'VN' pour p
et 'VN' pour p
- Type de noeud 2 : les milieux des arêtes, 2 d.l. par noeud, 'VN' pour
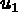 et
et 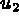
- Points et noeuds sont distincts : NCOPNP=0
- Fichier POBA : non nécessaire
- Blocage (S.D. BDCL) :
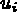 (noeud) = valeur
(noeud) = valeur
- Sous-programmes utilisateurs : oui
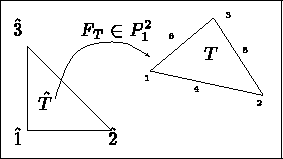
Figure: Elément TRIA P2P1
Coordonnées sur l'élément de référence:
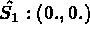
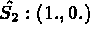
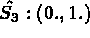
INTEGRATION NUMERIQUE
- -
- Intégration de surface: Intégration exacte aux 6 noeuds.
- npis=6
-
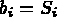 pour i=1,3, le sommet i de l'élément et pour i=4,6 les milieux des arêtes.
pour i=1,3, le sommet i de l'élément et pour i=4,6 les milieux des arêtes.
- -
- Intégration de bord: Intégration numérique à 3 points, les extrémités et le milieu de l'arête.
- npil=3
-
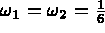 ,
, 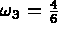
-
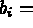 les 2 extrémité de l'arête concernée puis son milieu
les 2 extrémité de l'arête concernée puis son milieu
LES DONNEES A FOURNIR (en double précision)
- -
- S.D. MILI:
- -
- S.D. FORC: NDSM seconds membres.
- terme de surface
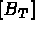 , partie
, partie 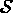
-
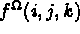 pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
- terme de bord
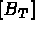 , partie
, partie 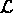
-
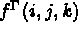 pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.
Remarques
-
Pour utiliser les sous-programmes utilisateurs, on fixera la valeur de NOTEL à la valeur ci-dessus en
ajoutant 20. Cette valeur est demandée lors de la
construction des S.D. MILI ou FORC (cf [Guide Modulef - 4]).
- La matrice du problème n'est pas définie positive. dans une factorisation de Gauss sans pivotement,
afin d'éviter un pivot nul, il est recommandé d'utiliser le module NUMXX (renumérotation) sur le maillage
créé.






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Suiv.: segm2por
Sup.: 9 Fiches techniques
Préc.: pent3r2c
Index
Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
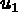 et
et 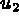 , les déplacements (ou vitesses) suivant x et y et la pression
, les déplacements (ou vitesses) suivant x et y et la pression
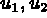 et 'VN' pour p
et 'VN' pour p
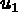 et
et 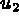
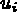 (noeud) = valeur
(noeud) = valeur
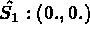
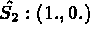
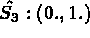
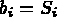 pour i=1,3, le sommet i de l'élément et pour i=4,6 les milieux des arêtes.
pour i=1,3, le sommet i de l'élément et pour i=4,6 les milieux des arêtes.
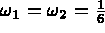 ,
, 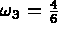
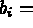 les 2 extrémité de l'arête concernée puis son milieu
les 2 extrémité de l'arête concernée puis son milieu
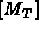 , partie
, partie 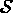
 la masse volumique supposée constante par élément.
la masse volumique supposée constante par élément.
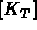 , partie
, partie 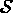
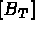 , partie
, partie 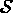
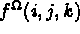 pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npis; la composante j du cas de charge i au point
d'intégration k.
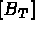 , partie
, partie 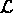
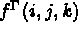 pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.
pour i=1,NDSM; j=1,2; k=1,npil; la composante j du cas de charge i au point
d'intégration k.