Suiv.: 2 Thermique bidimensionnelle Sup.: Le problème de la thermique Préc.: Généralités sur le traitement du Index Table des matières

Le système global

Pour obtenir le système à résoudre, il suffit de construire les matrices et seconds membres globaux qui s'écrivent, en notant 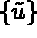le vecteur des degrés de liberté, regroupés noeuds par noeuds, comme:

Trouver 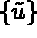vérifiant 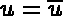sur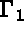

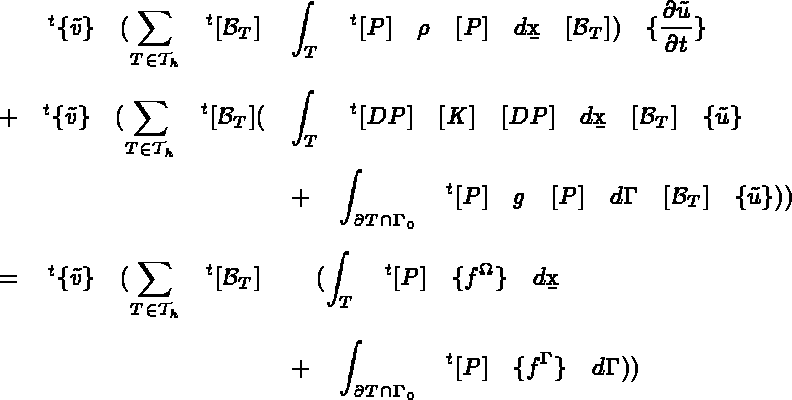
pour tout 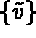tel que v= 0 sur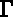

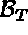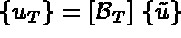avec la matrice permettant de passer de la numérotation locale à la numérotation globale i.e. . L'opération correspondante représente la phase d'assemblage; elle s'écrit, dans le cas de la matrice de rigidité par exemple, comme:

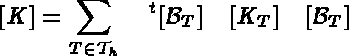
Le système ainsi obtenu peut être résolu par une méthode directe ou itérative (cf [Guide Modulef - 5]).