Suiv.: Modélisation en E.D.P. Sup.: Fiches techniques piézoélectriques Préc.: Fiches techniques piézoélectriques Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Modélisation en E.D.P.
Sup.: Fiches techniques piézoélectriques
Préc.: Fiches techniques piézoélectriques
Index
Table des matières
Le problème de la piézoélectricité (ou piézoélasticité) peut en fait être considéré comme une généralisation du problème de l'élasticité (voir chapitre 1). En effet, une céramique (ou un polymère) piézoélectrique est en fait un matériau élastique mais capable de coupler (de façon significative) les énergies élastiques et électriques. En d'autres termes, sous l'effet d'un champ électrique, une structure piézoélectrique sera le siège de champs de déformations et de contraintes induits (c'est un effet que l'on peut qualifier de moteur). Inversement, soumis à des efforts extérieurs conduisant à des champs de déformations et contraintes, la structure piézoélectrique produira un champ électrique induit (c'est l'effet capteur). On voit donc que pour prendre en compte ce phénomène, on a à introduire en plus des équations fondamentales utilisées en élasticité, les lois de comportement traduisant les couplages élastoélectriques, mais également l'équation au dérivées partielles régissant le comportement électrique.
On considère donc un domaine 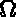 de
de 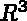 occupé par une structure
piézoélectrique dans son état initial (ou moyen si l'on travaille dans un
régime harmonique au cours du temps). On suppose que le milieu continu
est soumis à l'action de force de volume de densité
occupé par une structure
piézoélectrique dans son état initial (ou moyen si l'on travaille dans un
régime harmonique au cours du temps). On suppose que le milieu continu
est soumis à l'action de force de volume de densité 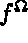 et à
l'action de forces de surface de densité
et à
l'action de forces de surface de densité 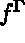 s'exerçant sur la partie
s'exerçant sur la partie
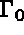 de la frontière
de la frontière 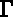 . On suppose de plus qu'une partie
. On suppose de plus qu'une partie
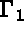 de cette frontière est encastrée et que
de cette frontière est encastrée et que  . De plus, le milieu est soumis à l'action de charges électriques
de densité surfacique q s'appliquant sur la partie
. De plus, le milieu est soumis à l'action de charges électriques
de densité surfacique q s'appliquant sur la partie 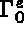 de
de 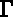 .
Enfin, on suppose que le potentiels électrique est imposé sur une partie
.
Enfin, on suppose que le potentiels électrique est imposé sur une partie
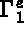 de
de 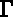 , telle que:
, telle que: 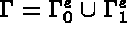 .
.
Le problème consiste en la détermination, à tout instant t, du champ des
déplacements 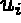 et du potentiel électrique
et du potentiel électrique 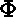 en tout point M
de
en tout point M
de 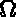 ainsi que le champ des contraintes
ainsi que le champ des contraintes 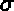 et éventuellement,
les densités de charges q sur
et éventuellement,
les densités de charges q sur 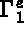 , ce à partir de la configuration
initiale donnée
, ce à partir de la configuration
initiale donnée 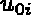 ,
, 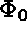 .
.