Suiv.: La méthode des éléments finis Sup.: Partie I: Introduction Préc.: Partie I: Introduction Index Table des matières

Modélisation mathématique d'un problème

De plus en plus d'équations aux dérivées partielles provenant de la modélisation de problèmes physiques très variés (en chimie, en thermique, en électromagnétisme, en mécanique du solide, en aérodynamique et pour des problèmes de mécanique des fluides, ...) sont résolues numériquement par la méthode des éléments finis.

La modélisation en équations aux dérivées partielles s'exprime formellement
[4] comme :

où u désigne les inconnues du problème, A un opérateur aux dérivées partielles, f une fonction donnée et 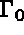une partie de la frontière.

Pour étudier mathématiquement ce problème il est plus commode d'utiliser une formulation variationnelle du problème. A un même problème peuvent correspondre plusieurs formulations variationnelles. Les éléments finis élastiques de la bibliothèque Modulef correspondent à des formulations variationnelles différentes : conforme, mixte, hybride ..., ce qui sera détaillé dans les paragraphes suivants.

Sous certaines conditions de régularité, le problème 1.1 s'écrit sous une forme variationnelle de la façon suivante :

où V est l'espace fonctionnel des fonctions admissibles, a(.,.) la forme bilinéaire associée à l'opérateur A et l(.) la forme linéaire associée à f. Cette formulation variationnelle est le point de départ d'une résolution par une méthode d'éléments finis.