Next: 2.2 Test 1: Thermal Problem Up: 2 Conversational tests Prev: 2 Conversational tests Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Next: 2.2 Test 1: Thermal Problem
Up: 2 Conversational tests
Prev: 2 Conversational tests
Contents
In this section we give an introductory example of how a problem is solved with the aid of the conversational programs in the MODULEF library.
Consider the following boundary value problem:
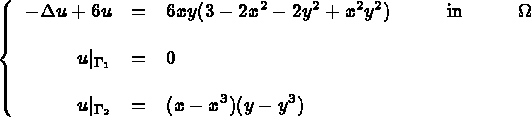
 , and the boundaries,
, and the boundaries,  and
and  , are described in figure 2.1
, are described in figure 2.1
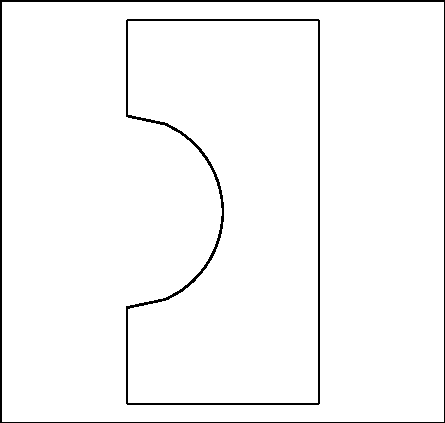
Figure 2.1: An introductory example
The exact solution to the above problem is given by:
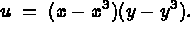
We solve this problem utilizing straight and curved finite elements of degree 2 (elements TRIA 2P2D and TRIA 2P2C of the THER library).
Following the steps in section 1.1.3, we will create all the relevant data files interactively, execute the modules corresponding to the various steps, and finally complete this example by investigating the accuracy of the numerical solution compared to the exact solution and conclude with a plot of the isovalues.
The preprocessor APNOXX is utilized to create the data and run the 2D mesh generator module, APNOPO. A call to APNOXX generates a main menu with three options:
A formatted data file is created interactively by responding to the "CREATE option on the main menu, i.e., by typing the letter "C" on your keyboard.
Remember: CAPITALS only!
You will now be confronted with various questions and prompts, to which you must respond by entering the appropriate keyword, data, etc. You can also specify how much screen output you would like when executing the module (for debugging purposes for example) by choosing a value of IMPRE between 0 and 10, where 0 indicates no output, and 10 indicates maximum output. Additional information is obtained by entering a " Y " to the " HELP " prompt. The input parameters pertaining to the example under consideration are indicated in brackets.
A copy of the entire process, i.e., creation of data files and execution and results, is included in each step in order to facilitate getting acquainted with the various MODULEF modules.
The input is described in detail below:
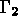 is defined with the aid of a function parser, i.e., by specifying
" Y " to the prompt
is defined with the aid of a function parser, i.e., by specifying
" Y " to the prompt
Additional information is output by entering " ? ".
The first data values to be specified are:
 IMPRE
IMPRE  10), and
10), and
A curve is defined by a number (from 1 to 99) which is associated with each curve equation. These curve numbers serve as line, or side, reference numbers (for keywords LIGN, and RETR, respectively). Therefore, in this example, the curve is designated by reference number 2, and the straight lines by reference number 1.
Each curve must then be defined as follows:
|
|
As before, we specify:
Each line is defined by specifying:
if NFFRON = 0 then the line is a straight line connecting NEXTR1 to NEXTR2
(ex: NFFRON = 0 for lines 1, 2, 3, 4, and 6), or
if NFFRON = -1 then the intermediary points are entered manually, or
if NFFRON = -2 , then the line is the portion of a circle centered at the origin
and passing through points NEXTR1 and NEXTR2, or
if NFFRON = -3 then the line is the portion of a circle centered at a specified point
and passing through points NEXTR1 and NEXTR2, and
Note: Additional information is obtained by entering a " Y " to the " HELP " prompt.
Keywords POIN and LIGN must have been executed before.
The four sides of the quadrangle are defined by:
|
|
Note: The number of points per line is equal on opposite sides.
The following data must be entered:
A list of the lines that form the contour is entered as follows:
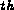 line of the contour, in an anti-clockwise direction
line of the contour, in an anti-clockwise direction
And lastly the following data values must be specified:
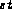 side. This number
defines the four sides of the quadrangle. (ex: 5), and
side. This number
defines the four sides of the quadrangle. (ex: 5), and
This keyword can only be activated after all the previous ones.
The following data must be input:
This keyword comes at the end of the process, just before keywords SAUV and FIN.
The following values must be specified:
This keyword can be activated at any moment to save part or whole of mesh.
The following data values must be stipulated:
Once the data file is created, we are ready to generate the corresponding mesh. This is achieved be choosing option EXECUTE from the main menu.
The input consists only of the following:
Some output will appear on your screen, depending on the value of the output parameter IMPRE. After execution you are returned to the main menu from which you can exit by typing " END ".
A printout of the data generation process and the screen output resulting from the execution is given below:
B$ apnoxx
****************
EXECUTING APNOPO : ( 2D MESH )
****************
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
C
-- TITLE OF THE JOB ( 20 CHARACTERES AT MOST ) ?
'TEST EXAMPLE'
**************************************************************************
CONVERSATIONAL CREATION OF DATA IN APNOPO
**************************************************************************
** WRITE IN CAPITALS PLEASE
-- NAME OF DATAFILE TO CREATE (A) ?
NOPO.DATA
-- HELP (YES-NO) ?
N
-- ARE YOU USING A FUNCTION PARSER (YES-NO-?) ?
Y
-- HELP (YES-NO) ?
N
-- IMPRE NFONC ?
1 1
THE 1 CURVES ARE NUMBERED FROM 1 TO 1 (YES-NO) ?
N
** ENTER THE EXPRESSION F(X,Y) ( = 0. ) ENDING WITH ;
** MAXIMUM LENGHT A64 ( 64 SPACES )
** EXAMPLE :' X**2 + Y**2 - 4;'
OR : X*X+Y*Y-4;
NUMBER OF CURVE 1 ?
2
-- CURVE 1 WITH NUMBER 2 :
X**2+Y**2-0.25;
-- KEYWORD ?
POIN
-- HELP (YES-NO) ?
N
-- IMPRE NPOINT ?
1 6
-- POINT NUMBER 1 : NOREF X Y ?
1 0 -1
-- POINT NUMBER 2 : NOREF X Y ?
1 1 -1
-- POINT NUMBER 3 : NOREF X Y ?
1 1 1
-- POINT NUMBER 4 : NOREF X Y ?
1 0 1
-- POINT NUMBER 5 : NOREF X Y ?
1 0 0.5
-- POINT NUMBER 6 : NOREF X Y ?
1 0 -0.5
-- REMAIN IN THIS KEYWORD (YES-NO) ?
N
-- KEYWORD ?
LIGN
-- HELP (YES-NO) ?
N
-- IMPRE NDLM ?
1 6
-- LINE NUMBER 1 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
5 1 2 1 0 1
-- LINE NUMBER 2 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
10 2 3 1 0 1
-- LINE NUMBER 3 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
5 3 4 1 0 1
-- LINE NUMBER 4 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
3 4 5 1 0 1
-- LINE NUMBER 5 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
6 6 5 2 10 1
** THE FUNCTION WITH INDEX 2 DESCRIBS LINE 5
-- LINE NUMBER 6 : NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON ?
3 6 1 1 0 1
-- REMAIN IN THIS KEYWORD (YES-NO) ?
N
-- KEYWORD ?
QUAC
-- HELP (YES-NO) ?
N
-- IMPRE NIVEAU NUDSD NBRELI NS1L ?
1 1 1 6 1
-- NOLO( 1) ?
1
-- NOLO( 2) ?
2
-- NOLO( 3) ?
3
-- NOLO( 4) ?
4
-- NOLO( 5) ?
5
-- NOLO( 6) ?
6
-- IMAX NQUAD ?
5 -1
-- DELETE (YES-NO) ?
N
-- KEYWORD ?
ADPO
-- HELP (YES-NO) ?
N
-- IMPRE NIVEA1 NIVEA2 N1 ISET ISEQ NOESOM ?
1 1 2 1 0 0 1
-- DELETE (YES-NO) ?
N
-- KEYWORD ?
RENC
-- HELP (YES-NO) ?
N
-- IMPRE NIVEA1 NIVEA2 ?
1 2 1
-- DELETE (YES-NO) ?
N
-- KEYWORD ?
SAUV
-- HELP (YES-NO) ?
N
-- IMPRE NINOPO NOM_NOPO NTNOPO ?
1 1 TEST.NOPO 0
-- DELETE (YES-NO) ?
N
-- KEYWORD ?
FIN
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
E
-- NAME OF THE DATA FILE ?
NOPO.DATA
-------------------------------------------------------------------------
COURBES
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD COUR
------------------------------
++ OPEN(11,FILE='',SPEC='SCRATCH,UNFORMATTED',RECL=0)
-------------------------------------------------------------------------
POIN
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD POIN
------------------------------
-------------------------------------------------------------------------
LIGN
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD LIGN
------------------------------
-------------------------------------------------------------------------
QUAC
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD QUAC
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE QUACOO : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
END OF MODULE QUACOO
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-------------------------------------------------------------------------
ADPO
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD ADPO
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE ADPNOP : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
END OF MODULE ADPNOP
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-------------------------------------------------------------------------
RENC
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD RENC
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE GIBBS : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE RENUM1 : TEST EXAMPLE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
RENUMBERING OF NODES
--------------------
NUMBER OF NODES : 171
------------------------------------------------------------------
I CHARACTERISTICS I BEFORE RENUMBERING I AFTER RENUMBERING I
------------------------------------------------------------------
I BAND WIDTH I 133 I 30 I
------------------------------------------------------------------
I TOTAL PROFILE I 11718 I 1998 I
I MEDIUM PROFILE I 68.526 I 11.684 I
------------------------------------------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
END OF MODULE RENUM1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
END OF MODULE GIBBS
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-------------------------------------------------------------------------
SAUV
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD SAUV
------------------------------
++ OPEN(12,FILE='test.nopo',SPEC='UNFORMATTED',RECL=0)
-------------------------------------------------------------------------
FIN
-------------------------------------------------------------------------
** PROCESSING OF KEYWORD FIN
------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
END OF MODULE APNOPO
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
END
The resulting data file, created by following the steps above, looks as follows:
'TEST EXAMPLE '
COURBES
1 $ IMPRE
COURBE02(X,Y)=
X**2+Y**2-0.25;
FIN
'POIN '
1 6 $ IMPRE NPOINT $
$ NOP NOREF(NOP) X(NOP). Y(NOP). $
1 1 0.000000E+00 -.100000E+01
2 1 0.100000E+01 -.100000E+01
3 1 0.100000E+01 0.100000E+01
4 1 0.000000E+00 0.100000E+01
5 1 0.000000E+00 0.500000E+00
6 1 0.000000E+00 -.500000E+00
'LIGN '
1 6 $ IMPRE NDLM $
$ NOLIG NOELIG NEXTR1 NEXTR2 NOREFL NFFRON RAISON $
1 5 1 2 1 0 0.100000E+01
2 10 2 3 1 0 0.100000E+01
3 5 3 4 1 0 0.100000E+01
4 3 4 5 1 0 0.100000E+01
5 6 6 5 2 10 0.100000E+01
6 3 6 1 1 0 0.100000E+01
'QUAC '
1 1 1 6 1 $ IMPRE NIVEAU NUDSD NBRELI NS1L
$ LIST OF THE CONTOUR LINES :
1 2 3 4 5 6
5 -1 $ IMAX NQUAD
'ADPO '
1 1 2 1 0 $ IMPRE NIVEA1 NIVEA2 N1 ISET
0 1 $ ISEQ NOESOM
'RENC '
1 2 1 $ IMPRE NIVEA1 NIVEA2
'SAUV '
1 1 0 $ IMPRE NINOPO NTNOPO
TEST.NOPO $ FILE NAME
'FIN '
The resulting mesh is stored in a data structure, under the name you specified when creating the data file, and can be plotted by calling the preprocessor TRNOXX, and specifying the D.S. NOPO file name, for example:
| Call preprocessor: | TRNOXX | |
| Specify data structure file name: | TEST.NOPO |
The resulting mesh is shown in figure 2.2.
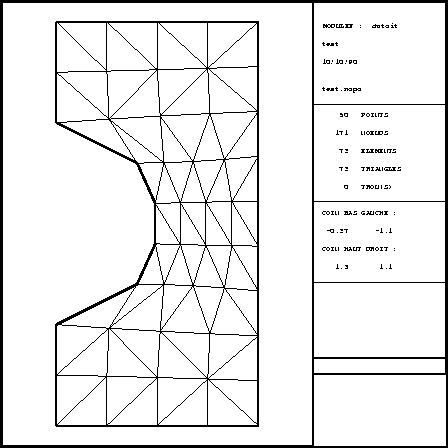
Figure 2.2: The mesh (plot generated by TRNOXX)
Now that you have successfully generated a mesh, stored in a D.S. NOPO, we may proceed to the next step.
Once the D.S. NOPO is created, we are ready to generate the interpolation functions. As discussed earlier, the example under consideration is a thermal type problem. We therefore choose finite element from the THERMAL library. We are concerned with a two-dimensional domain, and decide to use two-dimensional (2) straight (D) and curved (C) triangular (TRIA) finite elements with polynomial basis functions of degree 2 (P2 Lagrange), denoted TRIA 2P2D and TRIA 2P2C in the MODULEF library.
The preprocessor COMAXX is utilized to perform this step. As for step 1, the data file is created by choosing option CREATE from the main menu, and responding to the various prompts.
The input is described in detail below:
The curve data is input in exactly the same manner as in step 1.
A list of the available libraries can be obtained by typing a " ? " in response to the prompt " LIBRARY NAME ? ".
Type " ? " when in doubt.
Once the data file has been created we may execute this module by choosing option EXECUTE from the main menu.
The input is described below:
 IMPRE
IMPRE  10) must be specified (ex: 5).
10) must be specified (ex: 5).
The data creation procedure and the output corresponding to this step is printed below:
B$ comaxx
****************
EXECUTING COMACO : ( INTERPOLATION )
****************
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
C
**************************************************************************
CONVERSATIONAL DATA CREATION OF COMACO
**************************************************************************
-- NAME OF FILE TO CREATE ?
COMA.DATA
-- SPACE DIMENSION ?
2
-- ARE YOU USING A FUNCTIONS PARSER (YES-NO-?) ?
Y
PRINT PARAMETER (I) IMPRE
NUMBER OF CURVES TO DEFINE (I) NFONC
-- IMPRE NFONC ?
1 1
THE 1 CURVES ARE NUMBERED FROM 1 TO 1 (YES-NO) ?
N
** ENTER THE EXPRESSION F(X,Y) ( = 0. ) ENDING WITH ;
** MAXIMUM LENGHT A64 ( 64 SPACES )
** EXAMPLE :' X**2 + Y**2 - 4;'
OR : X*X+Y*Y-4;
CURVE NUMBER 1 ?
2
-- CURVE 1 WITH NUMBER 2 :
X**2+Y**2-0.25;
-- NUMBER OF SUB-DOMAINS ?
1
-- NUMBER OF REFERENCE NUMBERS ?
2
-- NUMBER OF CURVED LINES ?
1
-- NUMBER OF THE CURVED LINE : 1 ?
2
** CALL THE ELEMENT LIBRARY ( IDTECA=0 ) **
-- LIBRARY NAME ( NAME IN A4 OR ? ) ?
THER
-- NUMBER OF STRAIGHT ELEMENT TYPES IN THE SUB-DOMAIN: 1 ?
1
-- NAME OF THE STRAIGHT ELEMENT ( IN A4,1X,A4 OR ? ) ?
TRIA 2P2D
-- NUMBER OF CURVED ELEMENT TYPES IN THE SUB-DOMAIN : 1 ?
1
-- NAME OF THE CURVED ELEMENT ( IN A4,1X,A4 OR ? ) ?
TRIA 2P2C
-- FILE NAME OF THE INPUT D.S. NOPO ?
TEST.NOPO
-- FILE NAME OF THE OUTPUT D.S. MAIL ?
TEST.MAIL
-- FILE NAME OF THE OUTPUT D.S. COOR ?
TEST.COOR
-- ARE THERE TABLES TO ASSOCIATE (YES-NO) ?
N
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
E
-- NAME OF THE DATA FILE ?
COMA.DATA
-- PRINT PARAMETER OF THE D.S. ?
1
++ OPEN(11,FILE='test.nopo',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.mail',SPEC='UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.coor',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COMACO :
END OF MODULE COMACO
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TABLE M A I 2
--------------
SPACE DIMENSION (NDIM) : 2
NUMBER OF UNKNOWNS OF THE VARIATIONAL FORMULATION (NINCFV) : 1
NUMBER OF TYPES OF ELEMENTS (NTYELM) : 2
NUMBER OF REFERENCES (NNR) : 2
NUMBER OF TYPES OF NODES (NTYNOE) : 1
NUMBER OF TYPES OF POINTS (NTYPOI) : 1
NUMBER OF WORDS OF TABLE MAI3 (LMAI3) : 36
POINTS ARE ONLY DEFINED BY COORDINATES
NODES AND POINTS ARE NOT IDENTICAL (NCOPNP) : 0
MAX NUMBER OF WORDS FOR AN ELEMENT (NMMAEL) : 28
NUMBER OF WORDS OF THE TABLE MAIL (LMAIL) : 1421
STORAGE OPTION (NOPFI) : 0
TABLE C O O 2
-------------
TYPE OF THE TABLE COO4 (NTYT) : 2
NUMBER OF ITS INDEX (NINDI) : 2
SPACE DIMENSION (NDIM) : 2
MAX VALUE OF THE SECOND INDEX (M2) : 65
SEGMENTATION CODE (NCODS) : 1
NUMBER OF BLOCS (NBLOC) : 1
TYPE OF THE COORDINATE AXIS (NTACOO) : 1
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
END
The resulting data file is shown below:
1 $ USING THE FUNCTION PARSER
1 $ IMPRE
COURBE02(X,Y)=
X**2+Y**2-0.25;
FIN
2 1 0 $ NDIM NDSD NBSDC
2 1 $ NNR NBLC
2
THER $ LIBRARY NAME
1 $ NTYED OF SUB-DOMAIN 1
TRIA 2P2D $ THE NAME OF THE STRAIGHT ELEMENTS
1 $ NTYEC OF SUB-DOMAIN 1
TRIA 2P2C $ THE NAME OF THE CURVED ELEMENTS
TEST.NOPO $ FILE NAME
0 $ AND LEVEL OF THE D.S. NOPO
TEST.MAIL $ FILE NAME
0 $ AND LEVEL OF THE D.S. MAIL
TEST.COOR $ FILE NAME
0 $ AND LEVEL OF THE D.S. COOR
0 0 $ NTMAIL NTCOOR
Once the mesh is constructed and the interpolation is defined, it is necessary to enter the physical data of the problem under consideration. As discussed earlier in section 1.1.2, the present example can be solved in terms of the classical thermal problem by specifying some parameters in order to obtain a simplified system, which describes the problem under consideration. Thus, by specifying the following parameters
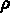
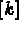
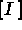 , a
, a 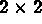 unit matrix,
unit matrix,
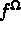
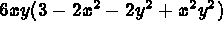 , and
, and
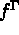
The data description is performed with preprocessor FOMIXX. We choose to define the function
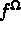 via the subroutine FORCEV and the rest of the data
via the subroutine FORCEV and the rest of the data 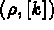 in array /CAR.
Subroutine FORCEV is printed below to aid you.
in array /CAR.
Subroutine FORCEV is printed below to aid you.
The input is described in detail below:
 ).
). The number of load cases, or RHS vectors, is given by:
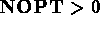 for a isotropic material, and
for a isotropic material, and 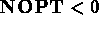 otherwise.
otherwise.
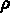 and [k] corresponding
to the mass and stiffness matrices respectively).
and [k] corresponding
to the mass and stiffness matrices respectively).
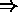 type 2, and
type 2, and  type 5 and
type 5 and
In the present example, to calculate (recall equations (1.7) and (1.8)):
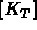 :
:
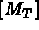 :
:
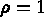 , and
, and
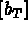 :
:
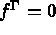 and
and 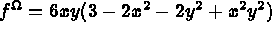 ,
,
If the data values do not enter the problem under
consideration, for example g and 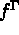 are zero, we may concatenate the data.
are zero, we may concatenate the data.
Thus, for the present example, we input only:
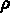 (ex: 1),
(ex: 1),
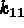 (ex: 1),
(ex: 1),
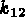 (ex: 0), and
(ex: 0), and
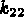 (ex: 1).
(ex: 1).
A comment, written between single quotes, must be input to describe the above array of data
You also have the opportunity to re-enter the data in the array under consideration.
After completing the data file you will be confronted with the main menu, from which you can choose to either create another data file (C), execute the module (E) once the data file is created, or terminate the process (END). Suppose that we choose to execute FOMIXX be typing a " E ", then the input data are the following:
 IMPRE
IMPRE  10) must be specified (ex: 5).
10) must be specified (ex: 5).
The data creation procedure is printed below, followed by the output generated by executing the preprocessor:
B$ fomixx
***************************
EXECUTING COFORC AND COMILI : ( DATA )
***************************
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
C
**************************************************
CONVERSATIONAL DATA CREATION FOR COFORC AND COMILI
**************************************************
-- NAME OF FILE TO CREATE (A) ?
FOMI.DATA
-- HELP (YES-NO) ?
N
-- NOMFIC (FORC) NIFORC NTFORC ?
TEST.FORC 1 0
-- NOMFIC (MILI) NIMILI NTMILI ?
TEST.MILI 1 1
** WE WILL DESCRIBE THE MANNER IN WHICH TO ENTER THE DATA
NECESSARY TO CALCULATE THE RHS VECTOR(S)
-- NDSM ?
1
-- PROCESSING BY GROUP (SUB-DOMAIN OR REFERENCE NUMBERS) (YES-NO) ?
Y
-- NDIM NDSD NBFR ?
2 1 0
SURFACE DATA S-D : 1 (YES-NO) ?
Y
OTHER INFORMATION (OYES-NO) ?
N
-- NOPT ITRAIT ( SURFACE REFERENCE : 1 ) ?
1 2
-- LOPT IADR ?
1 1
** DATA DESCRIPTION FOR THE MATRI(X)(CES)
NUMBER OF ASSOCIATED TABLES FOR THE D.S. MILI : 1
FOR EACH GIVEN TABLE ENTER:
ITS NAME (A) NOMTAB
ITS TYPE ( 1 TO 6 ) (I) NTYTAB
** INTEGER 1 , SP 2 , DP 5 , LOGICAL 3 , CHARACTER 4...
** HEAT PROBLEM : SINGLE PRECISION => TYPE 2
** ELASTICITY PROBLEM : DOUBLE PRECISION => TYPE 5
ITS NUMBER OF VARIABLES (I) NBVAR
** TABLE 1 ASSOCIATED WITH THE D.S. MILI
-- NOMTAB NTYTAB NBVAR ?
/CAR 2 4
** THE VARIABLES OF THE TABLE /CAR
-- /CAR( 1) = ?
1
-- /CAR( 2) = ?
1
-- /CAR( 3) = ?
0
-- /CAR( 4) = ?
1
** COMMENTS ABOUT THE TABLE /CAR
(60 CHARACTERS MAXI BETWEEN ')
'RO AND THE THERMAL CONDUCTIVITY'
-- RE-ENTER THE CHARACTERISTICS OF THE TABLE :/CAR (YES-NO) ?
N
-- PROCESSING BY GROUP (SUB-DOMAIN OR REFERENCE NUMBERS) (YES-NO) ?
Y
-- NDIM NDSD NBFR ?
2 1 0
SURFACE DATA S-D : 1 (YES-NO) ?
Y
OTHER INFORMATION (YES-NO) ?
N
-- NOPT ITRAIT ( SURFACE REFERENCE : 1 ) ?
1 1
-- NTABL IADR ?
/CAR 1
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
E
-- NAME OF DATA FILE (A) ?
FOMI.DATA
-- PRINT PARAMETER OF THE D.S. ?
1
++ OPEN(11,FILE='test.forc',SPEC='UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.mili',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COFORC :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
END OF MODULE COFORC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COMILI :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
END OF MODULE COMILI
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TABLE F O R 2
--------------
INFORMATION ( NUMBER OF SETS ) OR NOT ( 0 )
--------------------------------------------------
| | | |
| | SUB-DOMAINS | ELEMENTS |
| | | |
--------------------------------------------------
| VOLUMES | 0 | 0 |
| SURFACES | 1 | 0 |
| LINES | 0 | 0 |
| POINTS | 0 | 0 |
--------------------------------------------------
TABLE M I L 2
--------------
INFORMATION ( NUMBER OF SETS ) OR NOT ( 0 )
--------------------------------------------------
| | | |
| | SUB-DOMAINS | ELEMENTS |
| | | |
--------------------------------------------------
| VOLUMES | 0 | 0 |
| SURFACES | 1 | 0 |
| LINES | 0 | 0 |
| POINTS | 0 | 0 |
--------------------------------------------------
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
END
The resulting data file, generated by executing preprocessor FOMIXX, is shown below:
TEST.FORC $ FILE NAME OF THE D.S. FORC
1 0 $ ITS LEVEL AND NUMBER OF TABLES
TEST.MILI $ FILE NAME OF THE D.S. MILI
1 1 $ ITS LEVEL AND NUMBER OF TABLES
$ DATA RELATIVE TO THE D.S. FORC $
1 $ NDSM
0 1 0 0 0 0 0 0
1 0 1 2 $ NOSD NFRO NOPT ITRAIT
1 1 $ LOPT IADR
$ DATA RELATIVE TO THE D.S. MILI $
/CAR 2 4 $ NAME TYPE NBREMOT
0.100000E+01 $ /CAR( 1)
0.100000E+01 $ /CAR( 2)
0.000000E+00 $ /CAR( 3)
0.100000E+01 $ /CAR( 4)
' RO AND THE THERMAL CONDUCTIVITY ' $ CONTENTS
0 1 0 0 0 0 0 0
1 0 1 1 $ NOSD NFRO NOPT ITRAIT
/CAR 1 $ NTABL IADR
The user defined subroutine FORCE corresponding to the present example is printed below:
SUBROUTINE FORCEV(M,LOPT,X,NDIM,NPO,TAR,LTAR,LVECT,IADR,I1,
1 NARE,IA)
C.....................................................................
C AIM:
C INPUT THE HEAT QUANTITIES IN ORDER TO CALCULATE THE
C ELEMENT RHS VECTORS FOR A THERMAL PROBLEM.
C.....................................................................
C INPUT PARAMETERS:
C M SUPER ARRAY
C LOPT COFORC PARAMETER
C X ELEMENT COORDINATE TABLE
C NDIM DIMENSION
C NPO NUMBER OF POINTS FOR THE ELEMENT
C LTAR NUMBER OF WORDS OF THE ARRAY TAR FOR EVRY ELEMENT
C LVECT NUMBER OF SAME COLOR ELEMENTS
C IADR COFORC PARAMETER
C I1 0 USUALLY (SEE DOC 14)
C NARE FACE NUMBER (3D), EDGE NUMBER (2D)
C IA ADRESS -1 IN MAIL OF THE 1ST WORD OF THE CURRENT ELEMENT
C
C OUTPUT PARAMETERS:
C TAR ARRAY TAR(LTAR,LVECT)
C......................................................................
C
INTEGER M(*),IP(3)
REAL X(NPO,NDIM),TAR(*)
DATA IP/2,3,1/
IF (NPO .EQ. 3) THEN
C
C THE ELEMENT IS STRAIGHT
C
DO 1 I = 1, 3
XM = 0.5*(X(I,1)+X(IP(I),1))
YM = 0.5*(X(I,2)+X(IP(I),2))
TAR(I) = 6*XM*YM*(3-2*(XM**2)-2*(YM**2)+(XM**2)*(YM**2))
1 CONTINUE
ELSE IF (NPO.EQ. 6) THEN
C
C THE ELEMENT IS CURVED
C
DO 2 I = 1, 6
TAR(I) = 6*X(I,1)*X(I,2)*(3-2*X(I,1)**2-2*X(I,2)**2
+ +X(I,1)**2*X(I,2)**2)
2 CONTINUE
ELSE
C
C ERROR MESSAGE
C
IMPRIM = IINFO('I')
WRITE(IMPRIM,1000) 'ERROR FORCE'
STOP
END IF
1000 FORMAT(1X,A)
END
Comments: The two types of finite elements do not need the same amount of data. It is possible to distinguish between a straight element and a curved element by the number of points (3 for a straight element, 6 for a curved element).
The element arrays are created by preprocessor THELXX. The input data file is generated by choosing option CREATE from the main menu and supplying the relevant responses to the remaining options or questions.
The input is described in detail below:
There is a linear combination between mass/stiffness (ex: Y and 1). The coefficients are stored in a array, /LIN in this example, and contains the values (6, 1) (keeping in mind the variational formulation of our problem).
Having created the data file, we proceed by choosing option EXECUTE from the main menu. However, before being able to execute THELXX, subroutine FORCE must be compiled and linked to preprocessor THELXX.
The input is described below:
 IMPRE
IMPRE  10) must be specified (ex: 5).
10) must be specified (ex: 5).
The data creation procedure and screen output of preprocessor THELXX is given below:
B$ thelxx
****************
EXECUTING THELAS (NEW) : ( ELEMENT COMPUTATIONS )
****************
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
C
**************************************************************************
CONVERSATIONAL DATA CREATION OF THENEW
**************************************************************************
-- NAME OF FILE TO CREATE ?
TAE.DATA
-- FILE NAME OF THE INPUT D.S. MAIL ?
TEST.MAIL
-- FILE NAME OF THE INPUT D.S. COOR ?
TEST.COOR
-- FILE NAME OF OUTPUT D.S. TAE ?
TEST.TAE
-- ARE THERE ASSOCIATED TABLES (YES-NO) ?
N
-- DO YOU USE THE POBA FILE (YES-NO) ?
( BASIS POLYNOMIALS ... IN DIRECT ACCESS )
N
-- DO YOU USE THE D.S. MILI (YES-NO) ?
Y
-- FILE NAME OF THE INPUT D.S. MILI ?
TEST.MILI
-- DO YOU USE THE D.S. FORC (YES-NO) ?
Y
-- FILE NAME OF THE INPUT D.S. FORC ?
TEST.FORC
-- TYPE OF PROBLEM (NPROV) ?
1 : THERMAL , 2 : ELASTIC , 3 : STREAMLINES
1
-- COMPUTE THE MASS MATRIX (YES-NO) ?
Y
-- IT MAY BE DIAGONAL (YES-NO) ?
N
-- COMPUTE THE STIFFNESS MATRIX (YES-NO) ?
Y
-- COMPUTE THE RHS VECTORS (YES-NO) ?
Y
-- COMPUTE THE FLUX (YES-NO) ?
N
-- ARE THERE LINEAR MASS-STIFFNESS COMBINATIONS (YES-NO) ?
Y
-- NUMBER OF LINEAR MASS-STIFFNESS COMBINATIONS ?
1
-- NAME (4 CHARACTERS ) OF THE TABLE WITH THESE VALUES ?
/LIN
-- COEFFICIENTS OF COMBINATION NUMBER : 1 ?
6 1
-- FILE NAME OF COLOURS (NOMCOU) OR EMPTY
AND MAX LENGTH OF THE VECTORS (LVECT)
VIDE 1
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
E
!! YOU USE THE LAST VERSION OF THELAS
YOUR DATA FILE MUST END WITH :
-- NAME OF THE DATA FILE ?
TAE.DATA
-- PRINT PARAMETER ?
1
++ OPEN(11,FILE='test.mail',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.coor',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.tae',SPEC='UNFORMATTED',RECL=0)
++ OPEN(14,FILE='test.mili',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(15,FILE='test.forc',SPEC='OLD,UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE THENEW :
** WARNING READRE : ARRAY TRAV HAS ZERO LENGTH WITH ADRES SET TO 1
TABLE T A E 2
--------------
NUMBER OF ELEMENTS (NE) : 72
NUMBER OF NODES (NOE) : 171
NUMBER OF TABLES ASSOCIATED AT EACH ELEMENT (NTACE) : 2
MAX NUMBER OF NODES BY ELEMENT (NNOMAX) : 6
CONSTANT NUMBER OF D.O.F. BY NODES ( 0 IF NOT ) (ND) : 1
MAXIMUM NUMBER OF D.O.F. PER NODE (NDLMAX) : 1
NUMBER OF TYPES OF ELEMENTS (NTYELM) : 2
SUM OF THE NUMBER OF NODES OF THESE TYPES (LNOET) : 12
PROBLEM : 1 THERMAL, 2 ELASTIC, 3 OTHER (NPROV) : 1
REQUESTED OPTIONS (NOPTNT) : 0
NUMBER OF THE ASSOCIATED TABLE COLLECTING :
THE MASS MATRIX : 0
THE STIFFNESS MATRIX : 0
THE FIRST LINEAR COMBINATION : 1
THE LAST ONE : 1
THE RIGHT HAND SIDE(S) : 2
THE STRESSES OR THE FLOW : 0
END OF MODULE THENEW
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
END
The resulting data file is given below:
TEST.MAIL $ FILE NAME
1 $ AND LEVEL OF THE D.S. MAIL
TEST.COOR $ FILE NAME
1 $ AND LEVEL OF THE D.S. COOR
TEST.TAE $ FILE NAME
1 $ AND LEVEL OF THE D.S. TAE
0 $ NTTAE
0 $ 1 IF POBA IS USED , 0 IF NOT
1 $ 1 IF MILI IS USED , 0 IF NOT
TEST.MILI $ FILE NAME
1 $ AND LEVEL OF THE D.S. MILI
1 $ 1 IF FORC IS USED , 0 IF NOT
TEST.FORC $ FILE NAME
1 $ AND LEVEL OF THE D.S. FORC
1 $ NPROV
1 1 1 0 $ IOPT(*)
/LIN 1 $ L.C. TABLE NAME AND NUMBER OF L.C.
0.6000000E+01 0.1000000E+01 $ COEFFICIENTS OF THE L.C.
VIDE 1 $ NOMCOU LVECT
The implementation of the boundary conditions is performed by the preprocessor COBDXX. The data file is created by choosing the CREATE option from the main menu.
The input is described in detail below:
the format of these values (ex: 2)
2: single precision, or
5: double precision.
Thus, for the example under consideration:
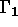 : u = 0 (ex: 0;), and
: u = 0 (ex: 0;), and
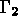 :
: 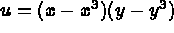
We are now ready to execute (E) COBDXX, after which we exit from this preprocessor by typing " END ".
The input is described below:
 IMPRE
IMPRE  10) must be specified (ex: 5).
10) must be specified (ex: 5).
The data creation procedure and output generated by preprocessor COBDXX are shown below:
B$ cobdxx
****************
EXECUTING COBDC1 : ( BOUNDARY CONDITIONS )
****************
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
C
**************************************************************************
CONVERSATIONAL DATA CREATION OF COBDC1
**************************************************************************
-- NAME OF FILE TO CREATE ?
BDCL.DATA
-- FILE NAME OF THE INPUT D.S. MAIL ?
TEST.MAIL
-- FILE NAME OF THE OUTPUT D.S. BDCL ?
TEST.BDCL
--THERE ARE ASSOCIATED TABLES (YES-NO) ?
N
-- THE RESTRICTED VALUES ARE :
1 ==> CONSTANTS , 2 ==> GIVEN BY FUNCTION ?
2
-- TYPE OF PRESCRIBED VALUES : 2 (SIMPLE) 5 (DOUBLE PRECISION) ?
2
-- WOULD YOU LIKE TO RESTORE THE D.S.E. MAIL TO GUIDE YOU (YES-NO) ?
Y
-- RESTRICT THE D.O.F. ON REFERENCE 1 (YES-NO) ?
Y
-- RESTRICT THE VARIATIONAL UNKNOWN : TEMPERATURE (YES-NO) ?
Y
** RESTRICTION OF THE MNEMONIC : VN
-- RESTRICT THE D.O.F. ON REFERENCE 2 (YES-NO) ?
Y
-- RESTRICT THE VARIATIONAL UNKNOWN : TEMPERATURE (YES-NO) ?
Y
** RESTRICTION OF THE MNEMONIC : VN
-- DO YOU USE THE FUNCTION PARSER (YES-NO) ?
Y
-- FILE NAME OF THE INPUT D.S. COOR ?
TEST.COOR
-- DO YOU USE THE COORDINATES OF THE NON-VERTEX POINTS (YES-NO) ?
Y
** ENTER THE EXPRESSION VALCLR(X,Y,Z) ENDING WITH ;
FOR BOUNDARY 1 FOR ITS UNKNOWN 1 FOR ITS MNEMONIC VN
** EXAMPLE :' X**2 + Y -1;'
OU : X**2+Y-1;
O;
** ENTER THE EXPRESSION VALCLR(X,Y,Z) ENDING WITH ;
FOR BOUNDARY 2 FOR THE UNKNOWN 1 FOR ITS MNEMONIC VN
(X-X*X*X)*(Y-Y*Y*Y);
-- THE NUMBER OF D.O.F. PER NODE IS CONSTANT (YES-NO) ?
Y
-- CONDITIONS BY LINEAR RELATIONS :
0 NO CONDITIONS
1 ENTERED MANUALLY ( < 20 )
-1 ENTERED BY SUBROUTINE SPCLRL
0
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
E
-- NAME OF DATA FILE ?
BDCL.DATA
-- PRINT PARAMETER FOR THIS D.S. ?
1
++ OPEN(11,FILE='test.mail',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.bdcl',SPEC='UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.coor',SPEC='OLD,UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CORNOE :
END OF MODULE CORNOE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COBDC1 :
END OF MODULE COBDC1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TABLE B D C 2
--------------
TYPE OF CONSTRAINED VALUES (NTYB) : 2
NUMBER OF CARDS DESCRIBING CONSTRAINTS (NCART) : 52
NUMBER OF LINEAR RELATIONS BETWEEN CONSTRAITS (NCLRL) : 0
STORAGE OPTION (NOPTFI) : 0
NUMBER OF WORDS OF TABLE BDC3 (NMMAT3) : 156
NUMBER OF WORDS OF TABLE BDC4 (NMMAT4) : 52
NUMBER OF WORDS OF TABLE BDC5 (NMMAT5) : 0
NUMBER OF WORDS OF TABLE BDC6 (NMMAT6) : 0
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
END
The resulting data file generated by the above procedure is printed below:
TEST.MAIL $ FILE NAME
35 $ AND LEVEL OF THE D.S. MAIL
TEST.BDCL $ FILE NAME
35 $ AND LEVEL OF THE D.S. BDCL
0 $ NTBDCL
2 2 2 $ ICONST NBFR NTYP
1 1 VN $ REF VARIATIONAL UNKN. MNEMO
2 1 VN $ REF VARIATIONAL UNKN. MNEMO
1 $ 1 IF USING FUNCTION PARSER
TEST.COOR $ FILE NAME
35 $ AND LEVELOF THE D.S. COOR
1 $ 1 IF D.S. COOR OF NODES
2 $ NUMBER OF FUNCTIONS
VALCLR01(X,Y,Z)=
O;
VALCLR02(X,Y,Z)=
(X-X*X*X)*(Y-Y*Y*Y);
FIN
0 $ 1 IF D.S. NDL1
0 $ 1 IF B.C. IN L.R. MANUALLY ;
$ -1 IF B.C. IN L.R. BY SUBROUTINE
After the boundary conditions are specified, the solution is computed by preprocessor CHOLXX. We first create the data file by choosing the CREATE option from the main menu.
The input is described in detail below:
the name of the file containing the I.D.S. BDCL must be entered (ex: TEST.BDCL).
There are no linear relations (ex: N).
We execute CHOLXX by choosing the EXECUTE option from the main menu.
The input is described below:
 IMPRE
IMPRE  10) must be specified (ex: 5).
10) must be specified (ex: 5).
A printout of the menu options, responses and results for preprocessor CHOLXX is given below:
B$ cholxx
**************************************
EXECUTING THE CHOLESKY SOLUTION METHOD
**************************************
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
C
**************************************************************************
CONVERSATIONAL DATA CREATION FOR THE CHOLESKY SEQUENCE (SEQUENTIAL)
**************************************************************************
-- NAME OF DATA FILE TO CREATE ?
B.DATA
-- FILE NAME OF THE INPUT D.S. MAIL ?
TEST.MAIL
-- NUMBER OF LOAD CASES (NDSM) ?
TYPE OF VALUES OF THE PROBLEM (NTYP) ?
1 2
-- NUMBER OF D.O.F. PER NODE IS CONSTANT (YES-NO) ?
Y
-- NUMBER OF DEGREES OF FREEDOM PER NODE ?
1
-- FILE NAME OF THE INPUT D.S. TAE ?
TEST.TAE
-- ARE THERE IMPOSED BOUNDARY CONDITIONS (YES-NO) ?
Y
-- FILE NAME OF THE INPUT D.S. BDCL ?
TEST.BDCL
-- ARE THERE LINEAR RELATIONS (YES-NO) ?
N
-- FILE NAME OF THE OUTPUT D.S. B ?
TEST.B
-- PRINT PARAMETER FOR THE SOLUTION ?
6
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
E
-- NAME OF DATA FILE ?
B.DATA
-- PRINT PARAMETER FOR THE EXECUTION ?
1
++ OPEN(11,FILE='test.mail',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(12,FILE='test.tae',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(13,FILE='test.bdcl',SPEC='OLD,UNFORMATTED',RECL=0)
++ OPEN(14,FILE='test.b',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE PREPAC :
NUMBER OF WORDS OF THE MATRIX (LMUA5) : 1998
MAX DIFFERENCE BETWEEN 2 NODES OF AN ELEMENT (LBDP) : 30
MAX DIFFERENCE BETWEEN 2 D.O.F. OF AN ELEMENT (LBDPDL) : 30
MAX NUMBER OF NODES PER ELEMENT (NNOMAX) : 6
NUMBER OF RHS VECTORS (NDSM) : 1
NUMBER OF WORDS IN C.M. FOR D.S. NDL1 (MCNDL1) : 0
NUMBER OF WORDS IN C.M. FOR D.S. MUA (MCMUA) : 2216
NUMBER OF WORDS IN C.M. FOR D.S. B (MCB) : 216
END OF MODULE PREPAC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE ASSMUA :
END OF MODULE ASSMUA
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE ASEMBV :
END OF MODULE ASEMBV
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CLIMPC :
END OF MODULE CLIMPC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CHOLPC :
END OF MODULE CHOLPC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE DRCHPC :
END OF MODULE DRCHPC
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
PRINT OUT OF D.S. B OF LEVEL 1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TITLE :
DATE AND USER'S NAME : 14/11/90 dutoit
DATA STRUCTURE TYPE : B
LEVEL AND STATE NUMBER : 1 2
NUMBER OF EXTRA TABLES : 0
TABLE B 2
----------
TYPE OF THE TABLE (NTYT) : 2
NUMBER OF INDICES AND THEIR MAXIMA (NIND..) : 2 1 171
OPTION ( 1:PAGES OF SAME SIZE , 0:IF NOT ) (NCOD) : 1
NUMBER OF PAGES OF THE TABLE B4 (NBLOC) : 1
NUMBER OF NODES (NOE) : 171
NUMBER OF TABLES B4 ON THIS D.S. (NBBLOC) : 1
CONSTANT NUMBER OF D.O.F. AT EACH NODE OR 0 (ND) : 1
NUMBER OF D.O.F. OR LENGHT OF A PAGE OF B4 (NTDL) : 171
STORAGE OPTION FOR B4 (NCODSB) : -1
TABLE B 3
----------
POINTER ON THE LAST ROW OF EACH PAGE OF B4
1 0 2 171
TABLE B4(NDSM,NTDL) NUMBER : 1
-----------------------------------
TABLE B4(NDSM,NTDL) PAGINATED IN 1 OR MORE PAGES
------------------------------------------------
PAGE 1
----------
------------------------------------------------------
| NODE | DOF | GLOBAL DOF| LOAD CASE(S) |
------------------------------------------------------
| 1 | 1 | 1 | 0.395995E-01
| 2 | 1 | 2 | 0.000000
| 3 | 1 | 3 | 0.633241E-01
| 4 | 1 | 4 | 0.000000
| 5 | 1 | 5 | 0.000000
| 6 | 1 | 6 | 0.000000
| 7 | 1 | 7 | 0.000000
| 8 | 1 | 8 | 0.000000
| 9 | 1 | 9 | 0.733093E-01
| 10 | 1 | 10 | 0.739653E-01
-- CREATE THE DATA =-= EXECUTE MODULE (DATA EXISTING) =-= END =-= ?
- - ---
END
The resulting data file generated by preprocessor CHOLXX is printed below:
TEST.MAIL $ FILE NAME
1 $ AND LEVEL OF THE D.S. MAIL
1 2 1 $ NDSM NTYP ND
TEST.TAE $ FILE NAME
1 $ AND LEVEL OF THE D.S. TAE
1 $ 1 IF BDCL IS USED , 0 IF NOT
TEST.BDCL $ FILE NAME
1 $ AND LEVEL OF THE D.S. BDCL
0 $ 1 IF B.C. IN LINEAR RELATIONS EXIST
TEST.B $ FILE NAME
1 $ AND LEVEL OF THE D.S. B
6 $ IMPREB
If the exact solution to the problem under consideration is known, we can use the post-processor NORMXX in order to determine the accuracy of the numerical solution, i.e., by calculating the error norms.
The input is described in detail below:
The following information must also be supplied:
The screen output generated by preprocessor NORMXX, is shown below.
B$ normxx
*************
EXECUTE NORME : ( TEST WITH AN EXACT SOLUTION )
*************
-- EXIT : 0 ?
-- NORM RELATIVE TO A D.S. B : 1 ?
-- " " TO A D.S. TAE : 2 ?
-- (STRESSES)
-- ENERGY NORM : 3 ?
1
-- FILE NAME OF THE INPUT D.S. MAIL ?
TEST.MAIL
-- FILE NAME OF THE INPUT D.S. COOR ?
TEST.COOR
-- FILE NAME OF THE INPUT D.S. B (SOLUTION) ?
%% THE D.S. B MUST BE IN SEQUENTIAL ACCESS
TEST.B
-- WOULD YOU LIKE TO STORE THE ERROR (YES-NO) ?
N
-- PRINT PARAMETER ?
6
-- WOULD YOU LIKE TO USE THE FUNCTION PARSER (YES-NO) ?
Y
-- DESCRIPTIVE FILE NAME OF FUNCTIONS
SOLUTION
++ OPEN(37,FILE='solution',SPEC='',RECL=0)
-- THIS FILE EXISTS ALREADY (YES-NO) ?
N
-- NUMBER OF DEGREES OF FREEDOM TO DESCRIBE ?
1
-- SOLUTION TYPE ( 2 IN SIMPLE PRECISION , 5 IN DOUBLE ) ?
2
** ENTER THE EXPRESSION SOLEX(X,Y,Z) ENDING WITH ;
FOR DEGREE OF FREEDOM : 1
** EXAMPLE :' X**2 + Y -1;'
OR : X**2+Y-1;
(X-X*X*X)*(Y-Y*Y*Y);
-- SCREEN OUTPUT (YES-NO) ?
Y
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE NORME :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
-------------------------------------------------------------------------
| NODE | DOF| GLOBAL DOF| MNEMO | EXACT SOL | CALCULATED SOL | % |
-------------------------------------------------------------------------
| 1 | 1 | 1 | VN | 0.39400E-01 0.39599E-01 | 101. |
| 2 | 1 | 2 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 3 | 1 | 3 | VN | 0.63040E-01 0.63324E-01 | 100. |
| 4 | 1 | 4 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 5 | 1 | 5 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 6 | 1 | 6 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 7 | 1 | 7 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 8 | 1 | 8 | VN | 0.00000E+00 0.00000E+00 | 100. |
| 9 | 1 | 9 | VN | 0.73171E-01 0.73309E-01 | 100. |
.
.
.
| 171 | 1 | 171 | VN | 0.00000E+00 0.00000E+00 | 100. |
-------------------------------------------------------------------------
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
PRINT OUT OF D.S. MAIL OF LEVEL 0
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TITLE :
DATE AND USER'S NAME : 14/11/90 dutoit
DATA STRUCTURE TYPE : MAIL
LEVEL AND STATE NUMBER : 0 0
NUMBER OF ASSOCIATED TABLES : 0
TABLE M A I 2
--------------
SPACE DIMENSION (NDIM) : 2
NUMBER OF UNKNOWNS OF THE VARIATIONAL FORMULATION (NINCFV) : 1
NUMBER OF TYPES OF ELEMENTS (NTYELM) : 2
NUMBER OF REFERENCES (NNR) : 2
NUMBER OF TYPES OF NODES (NTYNOE) : 1
NUMBER OF TYPES OF POINTS (NTYPOI) : 1
NUMBER OF WORDS OF TABLE MAI3 (LMAI3) : 36
POINTS ARE ONLY DEFINED BY THEIR COORDINATES
NODES AND POINTS DO NOT COINCIDE (NCOPNP) : 0
MAX NUMBER OF WORDS FOR AN ELEMENT (NMMAEL) : 28
NUMBER OF WORDS OF THE TABLE MAIL (LMAIL) : 1421
STORAGE OPTION (NOPFI) : 0
TABLE M A I 3
--------------
NUMBER OF ELEMENTS (NE) : 72
NUMBER OF NODES (NOE) : 171
NUMBER OF POINTS (NP) : 65
NUMBER OF SUB-DOMAINS (NDSD) : 1
*** TABLE OF THE TYPES OF ELEMENTS ***
--------------------------------------------------------------------------------
| S-D | NODE | SEGMENT | TRIANGLE | QUADRANGLE |
--------------------------------------------------------------------------------
| | STRAIGHT CURVED | STRAIGHT CURVED | STRAIGHT CURVED | STRAIGHT CURVED |
--------------------------------------------------------------------------------
| 1 | | | | |TRIA2P2D|TRIA2P2C| | |
--------------------------------------------------------------------------------
--------------------------------------------------------------------------------
| S-D | TETRAHEDRON | PENTAHEDRON | HEXAHEDRON | SUPER-ELEMENT |
--------------------------------------------------------------------------------
| | STRAIGHT CURVED | STRAIGHT CURVED | STRAIGHT CURVED | STRAIGHT CURVED |
--------------------------------------------------------------------------------
| 1 | | | | | | | | |
--------------------------------------------------------------------------------
TABLES M A I 5 TO M A I 8
-------------------------------
DESCRIPTION OF NODE TYPES
NUMBER OF VARIATIONAL UNKNOWNS FOR EACH NODE TYPE
-----------------------------------------------------
TYPE 1 : 1
NODE TYPE 1 :
--------------------
TEMPERATURE (UNKNOWN : 1) : VN
TABLES M A I B TO M A I K
-------------------------------
DESCRIPTION OF ELEMENT TYPES
ELEMENT TYPE 1 :
-------------------
ELEMENT NAME : THERTRIA2P2D
ELEMENT CODE : 100002
THE ELEMENT IS A : TRIANGLE
NUMBER OF NODES : 6
NUMBER OF POINTS : 3
NUMBER OF ASSOCIATED TABLES : 1
-------------------------------------------------------------------------------
| NODE | TYPE | COORDINATES ON THE UNIT ELEMENT |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
| 4 | 1 | 0.5000000 0.0000000
| 5 | 1 | 0.5000000 0.5000000
| 6 | 1 | 0.0000000 0.5000000
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
| POINT | TYPE | COORDINATES ON THE UNIT ELEMENT |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
-------------------------------------------------------------------------------
TABLE 1 ( TYPE ENTIER ) : 1 MAX VALUE OF INDEX(ES) : 7
ELEMENT TYPE 2 :
-------------------
ELEMENT NAME : THERTRIA2P2C
ELEMENT CODE : 100003
THE ELEMENT IS A : TRIANGLE
NUMBER OF NODES : 6
NUMBER OF POINTS : 6
NUMBER OF ASSOCIATED TABLES : 1
-------------------------------------------------------------------------------
| NODE | TYPE | COORDINATES ON THE UNIT ELEMENT |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
| 4 | 1 | 0.5000000 0.0000000
| 5 | 1 | 0.5000000 0.5000000
| 6 | 1 | 0.0000000 0.5000000
-------------------------------------------------------------------------------
-------------------------------------------------------------------------------
| POINT | TYPE | COORDINATES ON THE UNIT ELEMENT |
-------------------------------------------------------------------------------
| 1 | 1 | 0.0000000 0.0000000
| 2 | 1 | 1.000000 0.0000000
| 3 | 1 | 0.0000000 1.000000
| 4 | 1 | 0.5000000 0.0000000
| 5 | 1 | 0.5000000 0.5000000
| 6 | 1 | 0.0000000 0.5000000
-------------------------------------------------------------------------------
TABLE 1 ( TYPE ENTIER ) : 1 MAX VALUE OF INDEX(ES) : 7
DL ERROR ERROR NORME ERROR ERROR AT NODE
ABSOLUTE L2 RELATIVE L2 L2 SOLUTION RELATIVE L1 MAXIMUM
1 0.39979E-02 0.41671E-02 0.95940E+00 0.46745E-02 0.21462E+00 67
X = 0.934672 Y = -0.921138E-03
-- EXIT : 0 ?
-- NORM RELATIVE TO A D.S. B : 1 ?
-- " " TO A D.S. TAE : 2 ?
-- (STRESSES)
-- ENERGY NORM : 3 ?
0
Fortran STOP
The results are plotted with the aid of preprocessor TRMCXX. The plot shown in figure 2.3 is generated by calling preprocessor TRMCXX and specifying the file names in which the I.D.S. MAIL and I.D.S. COOR are stored. The isovalues are plotted by the same preprocessor, by selecting the appropriate option from the plot menu and entering the name of the file containing I.D.S. B. The resulting plot is shown in figure 2.4.
Comments: Note the difference between the mesh plot obtained with TRNOXX and the one obtained by TRMCXX. In the former the interpolation was not known.
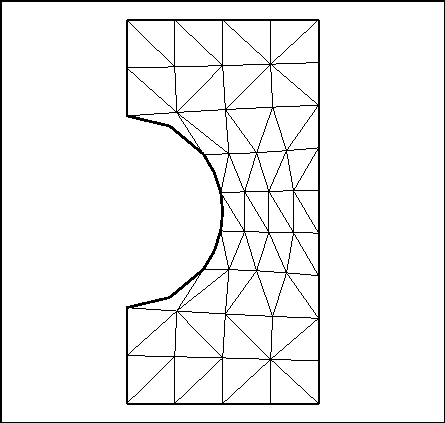
Figure 2.3: Mesh (plot generated by TRMCXX)
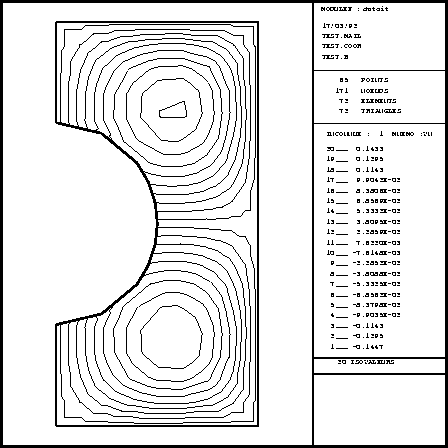
Figure 2.4: The isovalues (plot generated by TRMCXX)