Next: B List of preprocessors Up: Part IV: Appendices Prev: Part IV: Appendices Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Next: B List of preprocessors
Up: Part IV: Appendices
Prev: Part IV: Appendices
Contents
A list of the main modules available in the MODULEF library is given below. The modules can be grouped into the following logical units:
| APNOPO | D Mesh generator activated by a keyword. (super module) | ||
| CONOPO | D-3D manual mesh generator requiring a full description of each element. (via module APNOPO and APNOP3 with keyword "MANU") | ||
| TRIGEO | D mesh generator requiring a discretization of the contour of the domain (A. George method). (via APNOPO with keyword "TRIA") | ||
| TRIHER | D Voronoi mesh generator requiring a discretization of the contour of the domain (Voronoi, Delaunay, Hermeline). (via APNOPO with keyword "TRIH") | ||
| QUACOO | D mesh generator for a topologically quadrilateral domain.(via APNOPO with keyword "QUAC") |
| QUADRA | create a mesh consisting of quadrangles from mesh consisting of triangles (some triangles can be kept in the mesh) | ||
| APNOP3 | D mesh generator activated by a keyword.(super module) | ||
| COLIB2 | D mesh generator requiring a partitioning of the domain into coarse elements. | ||
| GEL3D1 | D mesh generator for a cubic topology from a finite difference type discretization in three directions. | ||
| MA2D3D | D mesh generator by stacking layers of a generic 2D surface.(via APNOP3 with keyword "MA23") | ||
| SYMNOP | Generate a mesh by symmetry w.r.t. a plane (3D) or a line (2D). (via APNOPO with keyword "SYMD" and APNOP3 with keyword " SYMP") | ||
| TRANOP | Mesh translation. (via APNOPO and APNOP3 with keyword "TRAN") | ||
| DILNOP | Anisotropic mesh dilation. (via APNOPO and APNOP3 with keyword "DILA") | ||
| DTRI3D | Split a 3D mesh composed of tetrahedral, pentahedral and hexahedral elements into tetrahedra.(via APNOP3 with keyword "TETR") | ||
| ROTNOP | Mesh rotation (via APNOPO and APNOP3 with keyword "ROTA") | ||
| MODNOP | Modify a mesh via one or more geometric transformations. (via APNOPO and APNOP3 with keyword "TRAN") | ||
| NOP2P1 | Transform a P2 mesh into a P1 mesh. | ||
| RETRIN |
Sub-divide a mesh by splitting each element into 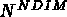 elements of the same type. (via APNOPO and APNOP3 with keyword "RETR") elements of the same type. (via APNOPO and APNOP3 with keyword "RETR") |
| RECOLC | Paste to meshes together to form one mesh. (via APNOPO and APNOP3 with keyword "RECO") | ||
| AIGUNO | Regularize (sharp angles) a 2D mesh containing only triangles (via APNOPO with keyword "AIGU") | ||
| REGMA2 | Regularize a 2D mesh by barycentre. (via APNOPO with keyword "REGU") | ||
| TN2D3D | Transform a 2D mesh into a 3D surface. (via APNOP3 with keyword "SU23") | ||
| TN3D2D | Transform a 3D mesh into a 2D mesh by setting the sides to zero. | ||
| AFFNOP | Refine a 2D mesh locally around some specified vertices. (via APNOPO with keyword "AFFL") | ||
| QUA4TR | Split the quadrangles of a 2D mesh into 4 triangles. (via APNOPO with keyword "Q4T") | ||
| TRCOAC | Extract the referenced sides and faces of a mesh. (via APNOPO and APNOP3 with keyword "EXTR") | ||
| ADPNOP | Define nodes (supports for degrees of freedom) if they differ from the vertices. (via APNOPO and APNOP3 with keyword "ADPO") | ||
| GIBBS | Renumber nodes or elements and nodes of a mesh. (via APNOPO and APNOP3 with keywords "RENE" or "RENC") | ||
| PROFIL | Renumber nodes or elements and nodes of a mesh (as for module GIBBS). (according to Marro's algorithm) | ||
| AKHHAT | Renumber nodes or elements and nodes of a mesh (as for module GIBBS). (according to Akhras Dhatt's algorithm) | ||
| RENUMT | Renumber the elements according to the increasing node numbers. | ||
| NUMMIX | Renumbering to avoid searching for pivots. | ||
| QUALNO | Measure the quality of mesh. |
| ISOPIE TRNOPO TRGEOM | Plot a 2D or 3D mesh. | ||
| CHARPO | Hinges between two beams. | ||
| CHARPL | Hinges between two plates. | ||
| INTERF | Create flat quadrangles on the referenced edges of a 2D DS NOPO. | ||
| WRNOPO | Write a DS NOPO using a coordinate file and a volumetric file. | ||
| NOTRP1 | Geometrically transform a DS NOPO containing Ruas triangles at 7 nodes into a P1 DS NOPO. | ||
| AXENOD | Calculate the nodal axes at each node construction of an array associated with the DS COOR |
| COMAC2 COMAC3 COMACO | Creates the data structures MAIL and COOR describing the mesh from a topological, metrical and interpolation point of view. | ||
| COFORC | Constructs the D.S. FORC which indicates where to find the necessary data for the calculation of the element right-hand-side vectors. | ||
| COMILI | Constructs the D.S. MILI which indicates where to find the information necessary (physical properties) to calculate the element matrices. | ||
| THENEW | Calculates the element matrices and RHS vectors and constructs the D.S. TAE. | ||
| THELAS | Calculates the element matrices and RHS vectors and constructs the D.S. TAE. (old version) | ||
| THERCT ELASCT | Replace COMILI, COFORC and THELAS, in thermal and elastic problems respectively, when the material characteristics, forces, or heat sources are constant by sub-domain or boundary section characterized by a reference number. |
| THEASS | Calculates and assembles the element matrices. | ||
| COTYNO | Construct the D.S. TYNO containing the significance of each d.o.f. calculated. | ||
| CTYTAE | Transforms a real D.S. TAE into a double precision D.S. TAE and vice versa. | ||
| CORNOE | Generates the D.S. COOR containing the nodal coordinates of the mesh. | ||
| BSPLIN | Approximate functions by B-Spline methods. | ||
| RECIPE | Recuperate the interpolation variable numbers corresponding to the finite element under consideration. |
| COBDC1 COBDCL | Constructs the D.S. BDCL which describes the constrained degrees of freedom. | ||
| CONDL1 | Constructs the D.S. NDL1 which contains nodal pointers for the case when the number of degrees of freedom per node is not constant. |
| PREPAC | Calculates the pointers of a skyline matrix. | ||
| ASSMUA | Assembles a skyline matrix in main memory (m.m.). | ||
| ASMAPS | Assembles a skyline matrix in secondary memory (s.m.). | ||
| CHOLPC | Cholesky factorization in m.m. | ||
| CHOLPS | Cholesky factorization in s.m. |
| ASEMBV | Assembles the RHS vectors in m.m. | ||
| ASMBMS | Assembles the RHS vectors in s.m. | ||
| CLIMPC | Incorporation of boundary conditions in m.m. | ||
| CLIMPS | Incorporation of boundary conditions in s.m. | ||
| DRCHPC | Solution of a linear system by forward- and back-substitution (CHOLESKY factorization) - skyline matrix - in m.m. | ||
| DRCHPS | As above, but in s.m. | ||
| PREPGC | Calculation of pointers for a compact matrix (for the conjugate gradient method). | ||
| ASSAMA | Assemble a matrix in m.m. in compact storage | ||
| DRGAPC | Solution of a linear system by forward- and back-substitution (GAUSS factorization) - skyline matrix - in m.m. | ||
| DRCRPC | Solution of a linear system by forward- and back-substitution (CROUT factorization) - skyline matrix - in m.m. | ||
| CROUPC | Crout factorization in m.m. | ||
| GAUSPC | Gauss factorization in m.m. | ||
| CLIMGC | Impose boundary conditions in m.m. for a linear system with a symmetric or non-symmetric compact matrix. | ||
| SIMPGC | Iterative solution of a linear system by conjugate gradient without preconditioning. | ||
| SSORGC | Iterative solution of a linear system by conjugate gradient with preconditioning by relaxation. | ||
| FANIGC | Incomplete factorization (CHOLESKY, CROUT) of a matrix. | ||
| ICHRGC | Iterative solution of a linear system by conjugate gradient with preconditioning of incomplete CHOLESKY or CROUT type. | ||
| CONDLU DGRADA | Solution of a non-symmetric linear system by the Accelerated Double Conjugate Gradient method. |
| RELAX | Solution of a linear system in m.m. by a relaxation method with automatic search of the optimal parameter. | ||
| PREPAF | Calculation of pointers for the frontal method. | ||
| FRONT | Solution by the GAUSS frontal method. | ||
| ADIMFE | Solution of a second order linear problem on a rectangle by RAVIART-THOMAS mixed elements (alternative directions of type UZAWA or ARROW-HURWITZ). |
| AMATB | Product of a compact matrix and a vector. | ||
| AMAT2 | Add 2 compact matrices. | ||
| CCAMAT | Delete matrix coefficients of an I.D.S. AMAT in m.m. not satisfying a certain condition. | ||
| CCMUA | Compress a D.S. MUA in m.m. | ||
| COSDB | Construct a D.S. B. | ||
| CSAMAT | Delete matrix coefficients of an I.D.S. MUA in m.m. or s.m. with direct access not satisfying a certain condition, and construct a corresponding O.D.S. AMAT. | ||
| MAXDLB | Print the extrema of a D.S. B. | ||
| MUABPC | Product of a skyline matrix and a vector. | ||
| MUA2PC | Add 2 skyline matrices. | ||
| BDISEQ | Store a D.S. B in s.m. with direct access in s.m. with sequential access or in m.m. | ||
| SDB2MC | Add 2 D.S. B in m.m. | ||
| SDB2MS | Add 2 D.S. B in s.m. |
| SYMBEL | Create the displacements corresponding to a symmetric domain. | ||
| UNIONB | Concatenate a 2 D.S. B into one. | ||
| TAMUA | Transform a D.S. AMAT into a D.S. MUA on a direct access file. | ||
| INVERD | Invert a matrix by complete Gauss pivoting. |
| ASSATR | Assemble element matrices into a full triangular matrix. | ||
| CLATRI | Impose boundary conditions. | ||
| FACTOS |
Factorize the matrix into 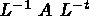 form. form. |
| SECINV | Secant method followed by inverse iteration with transformation. | ||
| SSPACE | Subspace (inverse)iteration method. | ||
| LANCZO | Calculate the smallest eigenvalues by LANCZOS with QR iteration. | ||
| ITEINV | Calculate the eigenvalues and vectors by inverse iteration with transformation. | ||
| QRMODU | Calculate all eigenvalues and corresponding vectors by the Householder-QR inverse iteration method. |
| STRESS | Calculate the stresses of a continuous medium. | ||
| FLUXTH | Calculate the flux or temperature. |
| ERREUR | Evaluate the sum of the element residues. | ||
| RECOLC | Paste two meshes, and their corresponding solution, together. | ||
| DEFNOP | Create a deformed mesh from the displacements and an initial mesh (elasticity problem). | ||
| NORME | Compare exact solutions with computed solutions for test problems with analytically known solutions. | ||
| NORTAE | As above, but the solution is stored in a D.S. TAE. | ||
| COMTAE | Compress the D.S. TAE resulting from STRESS to plot the stresses more quickly. | ||
| FOINRE | Calculate the stress loads on the contour of a sub-domain. |
| TRNOPO | Plot a 2D (and 3D interactively) mesh, and deformations in elasticity (via TRNOXX interactively, or BANOPO in batch). | ||
| TRGEOM | Plot a 3D mesh and deformations in elasticity (via TRNOXX interactively, or BAGEOM in batch). | ||
| TRMACO |
Plot a 2D mesh and/or plot:
| ||
| TRMC3G |
Plot a 3D mesh and/or plot:
|
| TRAKOU | Plot curves. (via TRACXX interactively) | ||
| TRISO3 | Plot isovalues in 3D on a plane of the cut. (via COUPXX interactively) | ||
| TRSTRE |
Plot a 2D mesh and/or plot stresses:
| ||
| TRFLUX |
Plot a 2D mesh and/or
| ||
| ISOPIE | Plot a 2D mesh and level lines of the pressure or piezometric head. (via ISOPXX interactively, or BAISOP in batch) | ||
| TRPOIN | Plot the characteristic points and lines of a 2D mesh. (via TRPOXX interactively) | ||
| PRMUAM TRAKOU | Plot the profile of a matrix MUA (skyline) or AMAT (compact). (via TRPRXX interactively, and BAPROF in batch) | ||
| V3DFXY | Plot a surface, z=f(x,y), by orthogonal sections. (via VIS3XX interactively) |
| TRANSI | Solve a time-dependent problem of type thermal or elastic. | ||
| EVOLGE EVOFGE | Solve a time-dependent problem by a multi-step predictor-corrector method by GEAR with automatic adjustment of the order (1 to 6) and the time-step. |
| EVOLRK EVOFRK | Solve a time-dependent problem by a Runga-Kutta method of order 3, improved by Alexander. | ||
| EVOLMP EVOFMP | Solve a time-dependent problem by a classical multi-step method of order 1 to 4. | ||
| EVOL2P EVOF2P | Second-order time multi-step method with damping. |
The difference between xxxLxx and xxxFxx resides in the fact that the matrices are constant or variable as a function of time.
| NSNCST NSNCEV | Solve the two-dimensional Navier-Stokes equations for a viscous incompressible fluid by approximation of non-conforming elements of zero base divergence. | ||
| NSNCPR | Calculate the pressure from the above results. | ||
| NSKINC | Solve the 2D Navier-Stokes equations by the alternate directions method. The non-linearity is solved by a least squares and conjugate gradient method. | ||
| NSPOAX | Solve the axisymmetric Navier-Stokes equations. | ||
| DAMIAN | Calculate the incompressible fluid flow in a porous medium. | ||
| NSQ2CA PRP1Q2 | Solve the two-dimensional non-stationary Navier-Stokes equations. The convection is treated by a characteristic method and a zero divergence base is used to treat the incompressibility. |
| SIGELA | Solve a unilateral contact problem without friction (Signorini problem and Winkler-Westergaard solid) by an iterative algorithm. |
| ELAPLA | Calculate the stresses in two- or three-dimensional elasto-plasticity. | ||
| TRSTRE | Plot the plastic zones. | ||
| COTAE GDEFIN PRELA3 |
Solve two or three-dimension large deformation hyper-elastic problems:
| ||
| TORBIN | Solve a BINGHAM fluid flow problem in a cylindrical container (elasto-plastic torsion). (This module is integrated in the non-linear elasticity library.) |
| COMPL | Solve variational inequalities where the solution is bounded by complementarity. | ||
| RELAX COMPRX | As above, but by relaxation. |
| BIHAP1 BIHAP2 DEDIRI FACMAF GRADCO PRCOL | Solve a Dirichlet problem for a biharmonic operator by a mixed finite element method of order 1 or 2. |
| PRSDOM SDOMVR SDOMVD | Decomposition of domains, respectively: construction of the operators; single precision iterative Algorithm; double precision iterative Algorithm. |
| GENE2D | Composite reinforced by unidirectional fibres: data generation for RESO2D | ||
| RESO2D | Composite reinforced by unidirectional fibres: calculation of the characteristics. | ||
| VISU2D | Composite reinforced by unidirectional fibres: visualization of the micro-stresses in the composite. |