Next: 3.3 Extrusion method (cylindrical topology) Up: 3.2 Multi-block method Prev: 3.2.5 Preprocessor COLIXX Index Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Next: 3.3 Extrusion method (cylindrical topology)
Up: 3.2 Multi-block method
Prev: 3.2.5 Preprocessor COLIXX
Index
Contents
The following examples are given:
The calling program of COLIB2, for a pentahedral element, is given below. Figure 3.3 shows
the mesh obtained for
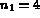 and
and 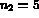 , where
, where 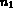 and
and 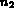 designate the number of points on the edges of the
triangular faces and the number of these points on the other edges, respectively.
designate the number of points on the edges of the
triangular faces and the number of these points on the other edges, respectively.
C ++++++++++++++++++++++++++++++++++++++++++++++
C TEST COLIBR ( COLIB2 WITH DATA FILE )
C ( A 2 DIMENSIONAL EXAMPLE )
C ++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 300000 )
COMMON M(LM)
C
IMPRE = -2
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
NFNOPO = 10
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'tunnel.nopo','UNKNOWN,UNFORMATTED',2000000)
C
NFDATA = 11
CALL TRUNIT (NFDATA)
CALL OUVRIS(NFDATA,'tunnel.data','UNKNOWN,FORMATTED',2000000)
C
CALL LECTEU(NFDATA)
CALL COLIBR(M,NFNOPO,NINOPO)
STOP
END
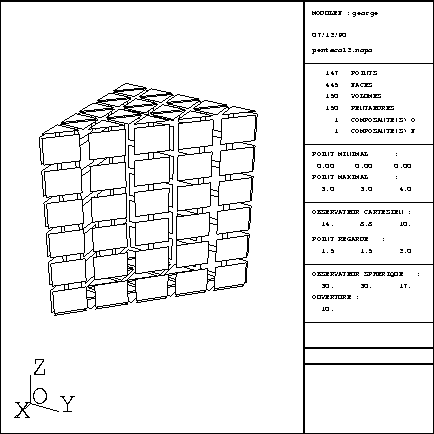
Figure 3.3: Mesh of a pentahedron via COLIB2
The calling program for COLIBR is shown below for the case corresponding to a 2D mesh construction from 17 triangular and quadrilateral blocks. The resulting mesh is shown in figure 3.4.
C ++++++++++++++++++++++++++++++++++++++++++++++
C TEST COLIBR ( COLIB2 WITH DATA FILE )
C ( A 2 DIMENSIONAL EXAMPLE )
C ++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 300000 )
COMMON M(LM)
C
IMPRE = -2
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
NFNOPO = 10
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'tunnel.nopo','UNKNOWN,UNFORMATTED',2000000)
C
NFDATA = 11
CALL TRUNIT (NFDATA)
CALL OUVRIS(NFDATA,'tunnel.data','UNKNOWN,FORMATTED',2000000)
C
CALL LECTEU(NFDATA)
CALL COLIBR(M,NFNOPO,NINOPO)
STOP
END
The data file required is the following:
$ NBS NA NBGRO IMPRE NBFR NDIM $
19 35 17 2 0 2
$ NOP NOREF X Y Z ? $
1 1 0.000000E+00 0.000000E+00 0.000000E+00
2 2 0.110000E+02 0.000000E+00 0.000000E+00
3 3 0.110000E+02 0.900000E+01 0.000000E+00
4 4 0.110000E+02 0.180000E+02 0.000000E+00
5 5 0.200000E+01 0.180000E+02 0.000000E+00
6 6 0.000000E+00 0.180000E+02 0.000000E+00
7 7 0.000000E+00 0.400000E+01 0.000000E+00
8 8 0.800000E+01 0.400000E+01 0.000000E+00
9 9 0.800000E+01 0.800000E+01 0.000000E+00
10 10 0.600000E+01 0.110000E+02 0.000000E+00
11 11 0.200000E+01 0.110000E+02 0.000000E+00
12 12 0.000000E+00 0.800000E+01 0.000000E+00
13 13 0.200000E+01 0.600000E+01 0.000000E+00
14 14 0.550000E+01 0.600000E+01 0.000000E+00
15 15 0.550000E+01 0.750000E+01 0.000000E+00
16 16 0.490000E+01 0.900000E+01 0.000000E+00
17 17 0.290000E+01 0.910000E+01 0.000000E+00
18 18 0.200000E+01 0.750000E+01 0.000000E+00
19 19 0.400000E+01 0.750000E+01 0.000000E+00
$ NA IEX1 IEX2 IDEC NP NOREF $
1 1 2 0 5 1
2 2 3 0 5 1
3 3 4 0 5 1
4 4 5 0 5 1
5 5 6 0 5 1
6 6 12 0 4 1
7 12 7 0 5 2
8 7 1 0 4 1
9 7 8 0 5 2
10 8 2 0 4 0
11 8 9 0 5 2
12 9 10 0 5 2
13 9 3 0 4 0
14 10 4 0 4 0
15 10 11 0 5 2
16 12 11 0 5 2
17 11 5 0 4 0
18 13 7 0 5 0
19 14 8 0 5 0
20 15 9 0 5 0
21 16 10 0 5 0
22 17 11 0 5 0
23 18 12 0 5 0
24 13 14 0 5 3
25 14 15 0 5 3
26 15 16 1 5 3
5.45 7.75 0.
5.4 8. 0.
5.3 8.25 0.
5.2 8.50 0.
5.1 8.75 0.
27 16 17 1 5 3
4.5 9.3 0.
4.25 9.45 0.
4.0 9.5 0.
3.5 9.45 0.
3.25 9.3 0.
28 17 18 1 5 3
2.60 8.75 0.
2.40 8.50 0.
2.25 8.25 0.
2.10 8.0 0.
2.05 7.75 0.
29 18 13 0 5 3
30 19 13 0 5 0
31 19 14 0 5 0
32 19 15 0 5 0
33 19 16 0 5 0
34 19 17 0 5 0
35 19 18 0 5 0
$ COARSE ELEMENTS $
$ I NCGE VERTICES NCGE NDSD $
1 4 1 2 8 7 4 1
2 4 2 3 9 8 4 1
3 4 3 4 10 9 4 1
4 4 10 4 5 11 4 1
5 4 11 5 6 12 4 1
6 4 7 13 18 12 4 2
7 4 7 8 14 13 4 2
8 4 8 14 15 9 4 2
9 4 15 9 10 16 4 2
10 4 16 10 11 17 4 2
11 4 18 17 11 12 4 2
12 3 13 14 19 3 3
13 3 14 15 19 3 3
14 3 15 16 19 3 3
15 3 16 17 19 3 3
16 3 19 18 17 3 3
17 3 13 19 18 3 3

Figure 3.4: 2D mesh via COLIBR
The calling program for COLIBR is given below for the case corresponding to the construction of a 3D mesh from 12 pentahedral and hexahedral blocks. The resulting mesh is shown in figure 3.5.
C ++++++++++++++++++++++++++++++++++++++++++++++
C TEST COLIBR ( COLIB2 WITH DATA FILE )
C ( A 3 DIMENSIONAL EXAMPLE )
C ++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 300000 )
COMMON M(LM)
C
IMPRE = -2
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
NFNOPO = 10
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'parttun.nopo','UNKNOWN,UNFORMATTED',2000000)
C
NFDATA = 11
CALL TRUNIT (NFDATA)
CALL OUVRIS(NFDATA,'parttun.data','UNKNOWN,FORMATTED',2000000)
C
CALL LECTEU(NFDATA)
CALL COLIBR(M,NFNOPO,NINOPO)
STOP
END
The data file required is the following:
$ NBS NA NBGRO IMPRE NBFR NDIM $
26 61 12 2 0 3
$ NOP NOREF X Y Z ? $
1 7 0.000000E+00 0.400000E+01 0.000000E+00
2 8 0.800000E+01 0.400000E+01 0.000000E+00
3 9 0.800000E+01 0.800000E+01 0.000000E+00
4 10 0.600000E+01 0.110000E+02 0.000000E+00
5 11 0.200000E+01 0.110000E+02 0.000000E+00
6 12 0.000000E+00 0.800000E+01 0.000000E+00
7 13 0.200000E+01 0.600000E+01 0.000000E+00
8 14 0.550000E+01 0.600000E+01 0.000000E+00
9 15 0.550000E+01 0.750000E+01 0.000000E+00
10 16 0.490000E+01 0.900000E+01 0.000000E+00
11 17 0.290000E+01 0.910000E+01 0.000000E+00
12 18 0.200000E+01 0.750000E+01 0.000000E+00
13 19 0.400000E+01 0.750000E+01 0.000000E+00
14 7 0.000000E+00 0.400000E+01 1.000000E+01
15 8 0.800000E+01 0.400000E+01 1.000000E+01
16 9 0.800000E+01 0.800000E+01 1.000000E+01
17 10 0.600000E+01 0.110000E+02 1.000000E+01
18 11 0.200000E+01 0.110000E+02 1.000000E+01
19 12 0.000000E+00 0.800000E+01 1.000000E+01
20 13 0.200000E+01 0.600000E+01 1.000000E+01
21 14 0.550000E+01 0.600000E+01 1.000000E+01
22 15 0.550000E+01 0.750000E+01 1.000000E+01
23 16 0.490000E+01 0.900000E+01 1.000000E+01
24 17 0.290000E+01 0.910000E+01 1.000000E+01
25 18 0.200000E+01 0.750000E+01 1.000000E+01
26 19 0.400000E+01 0.750000E+01 1.000000E+01
$ NA IEX1 IEX2 IDEC NP NOREF $
1 6 1 0 5 2
2 1 2 0 5 2
3 2 3 0 5 2
4 3 4 0 5 2
5 4 5 0 5 2
6 6 5 0 5 2
7 7 1 0 5 0
8 8 2 0 5 0
9 9 3 0 5 0
10 10 4 0 5 0
11 11 5 0 5 0
12 12 6 0 5 0
13 7 8 0 5 3
14 8 9 0 5 3
15 9 10 1 5 3
5.45 7.75 0.
5.4 8. 0.
5.3 8.25 0.
5.2 8.50 0.
5.1 8.75 0.
16 10 11 1 5 3
4.5 9.3 0.
4.25 9.45 0.
4.0 9.5 0.
3.5 9.45 0.
3.25 9.3 0.
17 11 12 1 5 3
2.60 8.75 0.
2.40 8.50 0.
2.25 8.25 0.
2.10 8.0 0.
2.05 7.75 0.
18 12 7 0 5 3
19 13 7 0 5 0
20 13 8 0 5 0
21 13 9 0 5 0
22 13 10 0 5 0
23 13 11 0 5 0
24 13 12 0 5 0
25 19 14 0 5 2
26 14 15 0 5 2
27 15 16 0 5 2
28 16 17 0 5 2
29 17 18 0 5 2
30 19 18 0 5 2
31 20 14 0 5 0
32 21 15 0 5 0
33 22 16 0 5 0
34 23 17 0 5 0
35 24 18 0 5 0
36 25 19 0 5 0
37 20 21 0 5 3
38 21 22 0 5 3
39 22 23 1 5 3
5.45 7.75 10.
5.4 8. 10.
5.3 8.25 10.
5.2 8.50 10.
5.1 8.75 10.
40 23 24 1 5 3
4.5 9.3 10.
4.25 9.45 10.
4.0 9.5 10.
3.5 9.45 10.
3.25 9.3 10.
41 24 25 1 5 3
2.60 8.75 10.
2.40 8.50 10.
2.25 8.25 10.
2.10 8.0 10.
2.05 7.75 10.
42 25 20 0 5 3
43 26 20 0 5 0
44 26 21 0 5 0
45 26 22 0 5 0
46 26 23 0 5 0
47 26 24 0 5 0
48 26 25 0 5 0
49 1 14 0 2 0
50 2 15 0 2 0
51 3 16 0 2 0
52 4 17 0 2 0
53 5 18 0 2 0
54 6 19 0 2 0
55 7 20 0 2 0
56 8 21 0 2 0
57 9 22 0 2 0
58 10 23 0 2 0
59 11 24 0 2 0
60 12 25 0 2 0
61 13 26 0 2 0
$ COARSE ELEMENTS $
$ I NCGE VERTICES NCGE NDSD $
1 7 1 2 8 7 14 15 21 20 7 1
2 7 2 3 9 8 15 16 22 21 7 1
3 7 3 4 10 9 16 17 23 22 7 1
4 7 10 11 5 4 23 24 18 17 7 1
5 7 5 6 12 11 18 19 25 24 7 1
6 7 1 7 12 6 14 20 25 19 7 1
7 6 7 8 13 20 21 26 6 2
8 6 8 13 9 21 26 22 6 2
9 6 13 9 10 26 22 23 6 2
10 6 13 10 11 26 23 24 6 2
11 6 13 11 12 26 24 25 6 2
12 6 7 13 12 20 26 25 6 2

Figure 3.5: 3D mesh via COLIBR
The following example illustrates the utilization of COLIBH for the case where the data is calculated, in the program, from a reduced set of parameters. The calling program of the module, which uses 2 subroutines, is given below, followed by a plot of the resulting mesh in figure 3.6.
C ++++++++++++++++++++++++++++++++++++++++++++++
C TEST COLIBH ( COLIB2 WITH A SINGLE HEXAHEDRA )
C ----------- EXAMPLE OF THE JUNCTION ( PART 1 )
C ++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 300000 )
COMMON M(LM)
INTEGER IDECAR(12),NBPARE(12)
REAL XYZ(3,8),XYZINT(3,200)
C
IMPRE = 3
NNN = 0
CALL INITIS(M,LM,IMPRE,NNN)
C --- THE O.D.S. NOPO ---
NFNOPO = 10
NINOPO = 0
CALL TRUNIT (NFNOPO)
CALL OUVRIS(NFNOPO,'joint1.nopo','UNKNOWN,UNFORMATTED',2000000)
C --- THE REFERENCES AND THE SUB-DOMAIN ---
NDSDE = 1
IREF = 1
C ------------------------
C --- THE GEOMETRY ---
C ------------------------
DO 1 I=1,3
DO 1 J=1,8
XYZ(I,J) = 0.
1 CONTINUE
C --- THE DEFINITION PARAMETERS :
RPI = 3.14159265
A30 = 30. * RPI / 180.
S30 = SIN(A30)
C30 = COS(A30)
R03 = 0.3
X03 = 0.
Y03 = 0.
R06 = 0.6
X06 = 0.
Y06 = 0.
BB = 1.2
C --- THE BASIS :
XYZ(1,1) = R06 * S30
XYZ(1,2) = R06 * S30
XYZ(1,3) = R03 * S30
XYZ(1,4) = R03 * S30
XYZ(2,1) = - R06 * C30
XYZ(2,2) = R06 * C30
XYZ(2,3) = R03 * C30
XYZ(2,4) = - R03 * C30
C --- THE TOP :
DO 2 I=1,2
DO 2 J=1,4
XYZ(I,J+4) = XYZ(I,J)
2 CONTINUE
DO 3 J=1,4
AA = 1.0 + 0.3 * XYZ(1,J) / 1.7
CALL SPELLI(AA,BB,XYZ(2,J+4),XYZ(3,J+4))
3 CONTINUE
C --- THE SIDES :
NPI = 5
DO 4 J=1,12
NBPARE(J) = NPI
IDECAR(J) = 0
4 CONTINUE
NBPARE(2) = 3
NBPARE(4) = 3
NBPARE(10) = 3
NBPARE(12) = 3
C
IDECAR(1) = 1
IDECAR(3) = 1
IDECAR(9) = 1
IDECAR(11) = 1
C --- THE INTERMEDIARY POINTS :
C EDGE 1 :
IEX11 = 1
IEX21 = 2
D1 = ( XYZ(2,IEX21) - XYZ(2,IEX11) ) / ( NPI + 1. )
C EDGE 3 :
IEX13 = 3
IEX23 = 4
D3 = ( XYZ(2,IEX23) - XYZ(2,IEX13) ) / ( NPI + 1. )
C Y
DO 5 J=1,NPI
XYZINT(2,J) = XYZ(2,IEX11) + J * D1
XYZINT(2,J+NPI) = XYZ(2,IEX13) + J * D3
5 CONTINUE
C X = FUNCTION OF Y
DO 6 J=1,NPI
CALL SPCERC(R06,X06,Y06,XYZINT(2,J),XYZINT(1,J))
CALL SPCERC(R03,X03,Y03,XYZINT(2,J+NPI),XYZINT(1,J+NPI))
6 CONTINUE
C SUPPORT ON THE EDGES 9 AND 11 :
DO 7 J=1,NPI
XYZINT(1,J+2*NPI) = XYZINT(1,J)
XYZINT(1,J+3*NPI) = XYZINT(1,J+NPI)
XYZINT(2,J+2*NPI) = XYZINT(2,J)
XYZINT(2,J+3*NPI) = XYZINT(2,J+NPI)
7 CONTINUE
C Z
DO 8 J=1,4*NPI
XYZINT(3,J) = 0.
8 CONTINUE
C Z ( EDGES 9 AND 11 )
DO 9 J=1,2*NPI
AA = 1.0 + 0.3 * XYZINT(1,J+2*NPI) / 1.7
CALL SPELLI(AA,BB,XYZINT(2,J+2*NPI),XYZINT(3,J+2*NPI))
9 CONTINUE
C --- CALL THE MODULE ---
CALL COLIBH(M,NFNOPO,NINOPO,XYZ,IDECAR,NBPARE,XYZINT,IREF,NDSDE)
STOP
END
C ++++++++++++++++++++++++++++++++++++++++++++++
C SPCERC
C ++++++++++++++++++++++++++++++++++++++++++++++
SUBROUTINE SPCERC(R,A,B,Y,X)
RES = R*R - ( Y - B ) * ( Y - B )
X = A + SQRT( RES )
END
C ++++++++++++++++++++++++++++++++++++++++++++++
C SPELLI
C ++++++++++++++++++++++++++++++++++++++++++++++
SUBROUTINE SPELLI(A,B,Y,Z)
Z = SQRT( 1. - Y*Y / ( A*A ) )
END
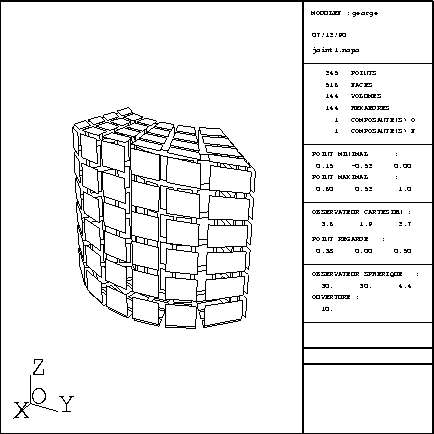
Figure 3.6: 3D mesh via COLIBH
The following example results from several calls to COLIBH, gluing the meshes obtained together, and different geometric manipulations of the latter (symmetries, rotations, etc., and a final gluing together).
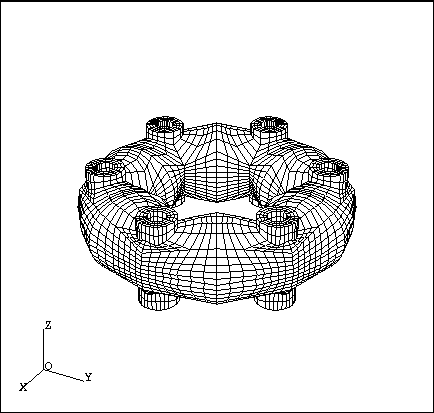
Figure 3.7: Mesh of a junction via COLIBH and geometric transformations