Next: 4 List of the modules Up: 3.4 Method for a hexahedral topology Prev: 3.4.3 Calling of module GEL3D1 Index Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Next: 4 List of the modules
Up: 3.4 Method for a hexahedral topology
Prev: 3.4.3 Calling of module GEL3D1
Index
Contents
As an illustration, we now give three examples, each of which is accompanied by a listing of the calling program, the output obtained during execution (with print parameter: IMPRE = 5) and a plot of the final mesh.
The first example is the mesh of a cube into tetrahedra. The data is equidistant (step h=0.4) in the 3 directions, with a single sub-domain number (- JOPTSD ) assigned. The final mesh is shown in figure 3.31.
The calling program is the following:
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
C EXAMPLE 1 : MODULE GEL3D1
C --------- ( PARALLELEPEDICAL DOMAIN ==> TETRAHEDRA )
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 18000 )
COMMON M(LM)
REAL H(1)
INTEGER NUMAT(1),ITYP(1)
EXTERNAL F1,F2,F3
C
IMPRE = 5
CALL INITIS(M,LM,IMPRE,0)
C ------ THE RESULTING FILE NOPO :
NFNOPO = 10
NINOPO = 0
CALL OUVRIR(NFNOPO,'GEL1.NOPO','UNFORMATTED',0,IOSTAT)
C ------ THE GEOMETRY :
N1 = 8
N2 = 7
NB = 4
H(1) = .4
IOPTM = 0
NOPTDE = 5
C ------ THE NUMBERS :
JOPTSD = -1
C
NFAUX = 0
C ------ CALL THE MODULE ------
CALL GEL3D1(M,IOPTM,JOPTSD,NOPTDE,N1,N2,NB,H,H,H,F1,F2,F3,
+ NUMAT,ITYP,NFNOPO,NINOPO,NFAUX)
END
The listing of the output obtained during execution is given below:
M M OOO DDDD U U L EEEEE FFFFF MM MM O O D D U U L E F M M M O O D D U U L EEEE FFFF M M O O D D U U L E F M M OOO DDDD UUU LLLLL EEEEE F VERSION 91 DATE : 18/10/91 AUTHOR : dutoit ++ OPEN(10,FILE='gel1.nopo',SPEC='UNFORMATTED',RECL=0) &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& MODULE GEL3D1 : &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& GENERATION OF 840 TETRAHEDRA AND 280 NODES LENGTH OF M (OVER-ESTIMATION) TO GENERATE NOPO : 17238 NUMBER OF POINTS IN X (NX) : 8 NUMBER OF POINTS IN Y (NY) : 7 NUMBER OF BANDS (NB) : 4 GENERATION OPTION (IOPT) : 0 NUMBERING OPTION OF THE D.S. (JOPT) : -1 SPLITTING OPTION (NOPT) : 5 STEP IN X (X(1)) : 0.4000E+00 STEP IN Y (Y(1)) : 0.4000E+00 STEP IN Z (H(1)) : 0.4000E+00 LENGTH CALCULATED OF M FOR D.S. NOPO 14726 END OF GENERATION OF NOPO ON FILE : 10 TABLE N O P 2 -------------- MESH CHARACTERISTICS : SPACE DIMENSION (NDIM ) : 3 MAXIMUM NUMBER OF REFERENCES (NDSR ) : 26 MAXIMUM NUMBER OF SUB-DOMAINS (NDSD ) : 1 NODES AND POINTS COINCIDE (NCOPNP) : 1 NUMBER OF ELEMENTS IN THE MESH (NE ) : 840 NUMBER OF TETRAHEDRA (NTET ) : 840 NUMBER OF BOUNDARY ELEMENTS (NEF ) : 640 NUMBER OF NODES (NOE ) : 280 NUMBER OF NODES PER SEGMENT (NO EXTREMITIES) : 0 TYPE OF COORDINATE VALUES (NTYCOO) : REEL1MOT MAX DIFFERENCE +1 BETWEEN 2 NODES OF AN ELEMENT : 64 NUMBER OF COARSE ELEMENTS (NBEGM ) : 0 NUMBER OF WORDS IN ARRAY NOP5 (LNOP5 ) : 13808 REFERENCE AXIS X,Y,Z (NTACOO) : 1 &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& END OF MODULE GEL3D1 &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&

Figure 3.31: First example of a mesh generated by GEL3D1
The second example is a mesh of a cube into hexahedra. The data consists of several bands of varying heights (array H(.)). Several sub-domain numbers are assigned (arrays ITYP and NUMAT). The final mesh is shown in figure 3.32.
The calling program is the following:
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
C EXAMPLE 2 : MODULE GEL3D1
C --------- ( PARALLELEPEDICAL DOMAIN ==> HEXAHEDRA )
C ( DIFFERENT HEIGHT BANDS, SEVERAL MEDIA )
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 18000 )
COMMON M(LM)
REAL X(7),Y(7),H(6)
INTEGER NUMAT(6,6,2),ITYP(5)
EXTERNAL F1,F2,F3
C
IMPRE = 5
CALL INITIS(M,LM,IMPRE,0)
C ------ THE RESULTING FILE NOPO :
NFNOPO = 10
NINOPO = 0
CALL OUVRIR(NFNOPO,'GEL2.NOPO','UNFORMATTED',0,IOSTAT)
C ------ THE GEOMETRY :
N1 = 7
X(1) = 0.
X(2) = 1.
X(3) = 1.5
X(4) = 2.
X(5) = 3.5
X(6) = 5.5
X(7) = 7.5
N2 = 7
Y(1) = 0.
Y(2) = 1.
Y(3) = 1.5
Y(4) = 2.
Y(5) = 3.
Y(6) = 4.
Y(7) = 5.
NB = 5
H(1) = 0.
H(2) = 1.
H(3) = 1.5
H(4) = 2.
H(5) = 3.
H(6) = 4.
IOPTM = 2
NOPTDE = 0
C ------ THE NUMBERS :
JOPTSD = 2
C ------ THE LAYER TYPES :
DO 1 I=1,5
ITYP(I) = 1
1 CONTINUE
ITYP(2) = 2
ITYP(3) = 2
C ------ THE SUB-DOMAINS :
DO 2 I=1,6
DO 2 J=1,6
DO 2 K=1,2
NUMAT(I,J,K) = 1
2 CONTINUE
NUMAT(4,4,1) = 2
NUMAT(4,4,2) = 3
C
NFAUX = 0
C ------ CALL THE MODULE ------
CALL GEL3D1(M,IOPTM,JOPTSD,NOPTDE,N1,N2,NB,X,Y,H,F1,F2,F3,
+ NUMAT,ITYP,NFNOPO,NINOPO,NFAUX)
END
The listing of the output during execution is given below:
M M OOO DDDD U U L EEEEE FFFFF MM MM O O D D U U L E F M M M O O D D U U L EEEE FFFF M M O O D D U U L E F M M OOO DDDD UUU LLLLL EEEEE F VERSION 91 DATE : 21/10/91 AUTHOR : dutoit ++ OPEN(10,FILE='gel2.nopo',SPEC='UNFORMATTED',RECL=0) &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& MODULE GEL3D1 : &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& GENERATION OF 180 HEXAHEDRA AND 294 NODES LENGTH OF M (OVER-ESTIMATION) TO GENERATE NOPO : 6684 NUMBER OF POINTS IN X (NX) : 7 NUMBER OF POINTS IN Y (NY) : 7 NUMBER OF BANDS (NB) : 5 GENERATION OPTION (IOPT) : 2 NUMBERING OPTION OF THE D.S. (JOPT) : 2 SPLITTING OPTION (NOPT) : 0 ABSCISSIS OF POINTS (X(*)) : 0.0000E+00 0.1000E+01 0.1500E+01 0.2000E+01 0.3500E+01 0.5500E+01 0.7500E+01 ORDINATES OF POINTS (Y(*)) : 0.0000E+00 0.1000E+01 0.1500E+01 0.2000E+01 0.3000E+01 0.4000E+01 0.5000E+01 HEIGHTS OF POINTS (H(*)) : 0.0000E+00 0.1000E+01 0.1500E+01 0.2000E+01 0.3000E+01 0.4000E+01 TYPE OF BANDS : 1 2 2 1 1 ARRAY NUMAT OF TYPE 1 : 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 ARRAY NUMAT OF TYPE 2 : 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 3 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 LENGTH CALCULATED OF M FOR D.S. NOPO 6684 END OF GENERATION OF NOPO ON FILE : 10 TABLE N O P 2 -------------- MESH CHARACTERISTICS : SPACE DIMENSION (NDIM ) : 3 MAXIMUM NUMBER OF REFERENCES (NDSR ) : 26 MAXIMUM NUMBER OF SUB-DOMAINS (NDSD ) : 3 NODES AND POINTS COINCIDE (NCOPNP) : 1 NUMBER OF ELEMENTS IN THE MESH (NE ) : 180 NUMBER OF HEXAHEDRA (NHEX ) : 180 NUMBER OF BOUNDARY ELEMENTS (NEF ) : 132 NUMBER OF NODES (NOE ) : 294 NUMBER OF NODES PER SEGMENT (NO EXTREMITIES) : 0 TYPE OF COORDINATE VALUES (NTYCOO) : REEL1MOT MAX DIFFERENCE +1 BETWEEN 2 NODES OF AN ELEMENT : 57 NUMBER OF COARSE ELEMENTS (NBEGM ) : 0 NUMBER OF WORDS IN ARRAY NOP5 (LNOP5 ) : 5724 REFERENCE AXIS X,Y,Z (NTACOO) : 1 &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& END OF MODULE GEL3D1 &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
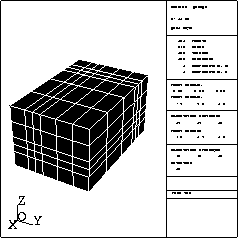
Figure 3.32: A second example of a mesh generated by GEL3D1
The third example is a mesh of a cube into pentahedra. The data is input via functions F1, F2 and F3, and a different sub-domain number is assigned to the layers (array NUMAT). The mesh obtained is shown in figure 3.33.
The calling program is the following:
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
C EXAMPLE 3 : MODULE GEL3D1
C --------- ( PARALLELEPEDICAL DOMAIN ==> PENTAHEDRA )
C ( UTILISATION OF THE 3 FUNCTIONS F1, F2 AND F3 )
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
PARAMETER ( LM = 30000 )
COMMON M(LM)
COMMON /CENTR/XC,YC,ANG
REAL X(8,5),Y(8,5),H(1)
INTEGER NUMAT(14,4),ITYP(1)
EXTERNAL F1,F2,F3
C
IMPRE = 5
CALL INITIS(M,LM,IMPRE,0)
C ------ THE RESULTING FILE NOPO :
NFNOPO = 10
NINOPO = 0
CALL OUVRIR(NFNOPO,'GEL3.NOPO','UNFORMATTED',0,IOSTAT)
C ------ THE GEOMETRY :
XC = -7.
YC = 0.
XPI = 3.141592654
ANG = XPI / 20.
C
N1 = 8
N2 = 5
XH1 = 2.
XH2 = 1.
DO 1 I=1,8
X(I,1) = ( I - 1 ) * XH1
X(I,5) = ( I - 1 ) * XH2 + 3.5
X(I,2) = .25 * ( 3.* X(I,1) + X(I,5) )
X(I,3) = .50 * ( X(I,1) + X(I,5) )
X(I,4) = .25 * ( X(I,1) + 3.*X(I,5) )
Y(I,1) = 0.
Y(I,2) = 1.5
Y(I,3) = 3.
Y(I,4) = 4.5
Y(I,5) = 6.
1 CONTINUE
NB = 20
IOPTM = 7
NOPTDE = 1
C ------ THE NUMBERS :
JOPTSD = 3
C ------ THE SUB-DOMAINS :
DO 2 I=1,14
DO 2 J=1,4
NUMAT(I,J) = 1
2 CONTINUE
NUMAT(5,2) = 2
NUMAT(5,3) = 2
NUMAT(6,3) = 2
NUMAT(7,3) = 2
C
NFAUX = 0
C ------ CALL THE MODULE ------
CALL GEL3D1(M,IOPTM,JOPTSD,NOPTDE,N1,N2,NB,X,Y,H,F1,F2,F3,
+ NUMAT,ITYP,NFNOPO,NINOPO,NFAUX)
END
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
C THE THREE FUNCTIONS F1, F2 AND F3
C ++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
FUNCTION F1(I,J,X,Y,K)
COMMON /CENTR/ XC,YC,ANG
F1 = XC + ( X - XC ) * COS( ( K - 1 ) * ANG )
END
FUNCTION F2(I,J,X,Y,K)
COMMON /CENTR/ XC,YC,ANG
F2 = Y
END
FUNCTION F3(I,J,X,Y,K)
COMMON /CENTR/ XC,YC,ANG
F3 = ( X - XC ) * SIN( ( K - 1 ) * ANG )
END
The listing of the output generated during execution is given below:
M M OOO DDDD U U L EEEEE FFFFF MM MM O O D D U U L E F M M M O O D D U U L EEEE FFFF M M O O D D U U L E F M M OOO DDDD UUU LLLLL EEEEE F VERSION 91 DATE : 21/10/91 AUTHOR : dutoit ++ OPEN(10,FILE='gel3.nopo',SPEC='UNFORMATTED',RECL=0) &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& MODULE GEL3D1 : &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& GENERATION OF 1120 PENTAHEDRA AND 840 NODES LENGTH OF M (OVER-ESTIMATION) TO GENERATE NOPO : 29758 NUMBER OF POINTS IN X (NX) : 8 NUMBER OF POINTS IN Y (NY) : 5 NUMBER OF BANDS (NB) : 20 GENERATION OPTION (IOPT) : 7 NUMBERING OPTION OF THE D.S. (JOPT) : 3 SPLITTING OPTION (NOPT) : 1 INITIAL COORDINATES GIVEN : X Y DE I,J 1 1 : 0.0000E+00 0.0000E+00 2 1 : 0.2000E+01 0.0000E+00 3 1 : 0.4000E+01 0.0000E+00 4 1 : 0.6000E+01 0.0000E+00 5 1 : 0.8000E+01 0.0000E+00 6 1 : 0.1000E+02 0.0000E+00 7 1 : 0.1200E+02 0.0000E+00 8 1 : 0.1400E+02 0.0000E+00 1 2 : 0.8750E+00 0.1500E+01 2 2 : 0.2625E+01 0.1500E+01 3 2 : 0.4375E+01 0.1500E+01 4 2 : 0.6125E+01 0.1500E+01 5 2 : 0.7875E+01 0.1500E+01 6 2 : 0.9625E+01 0.1500E+01 7 2 : 0.1138E+02 0.1500E+01 8 2 : 0.1313E+02 0.1500E+01 1 3 : 0.1750E+01 0.3000E+01 2 3 : 0.3250E+01 0.3000E+01 3 3 : 0.4750E+01 0.3000E+01 4 3 : 0.6250E+01 0.3000E+01 5 3 : 0.7750E+01 0.3000E+01 6 3 : 0.9250E+01 0.3000E+01 7 3 : 0.1075E+02 0.3000E+01 8 3 : 0.1225E+02 0.3000E+01 1 4 : 0.2625E+01 0.4500E+01 2 4 : 0.3875E+01 0.4500E+01 3 4 : 0.5125E+01 0.4500E+01 4 4 : 0.6375E+01 0.4500E+01 5 4 : 0.7625E+01 0.4500E+01 6 4 : 0.8875E+01 0.4500E+01 7 4 : 0.1013E+02 0.4500E+01 8 4 : 0.1138E+02 0.4500E+01 1 5 : 0.3500E+01 0.6000E+01 2 5 : 0.4500E+01 0.6000E+01 3 5 : 0.5500E+01 0.6000E+01 4 5 : 0.6500E+01 0.6000E+01 5 5 : 0.7500E+01 0.6000E+01 6 5 : 0.8500E+01 0.6000E+01 7 5 : 0.9500E+01 0.6000E+01 8 5 : 0.1050E+02 0.6000E+01 ARRAY NUMAT OF TYPE 1 : 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 LENGTH CALCULATED OF M FOR D.S. NOPO 28318 END OF GENERATION OF NOPO ON FILE : 10 TABLE N O P 2 -------------- MESH CHARACTERISTICS : SPACE DIMENSION (NDIM ) : 3 MAXIMUM NUMBER OF REFERENCES (NDSR ) : 26 MAXIMUM NUMBER OF SUB-DOMAINS (NDSD ) : 2 NODES AND POINTS COINCIDE (NCOPNP) : 1 NUMBER OF ELEMENTS IN THE MESH (NE ) : 1120 NUMBER OF PENTAHEDRA (NPENT) : 1120 NUMBER OF BOUNDARY ELEMENTS (NEF ) : 760 NUMBER OF NODES (NOE ) : 840 NUMBER OF NODES PER SEGMENT (NO EXTREMITIES) : 0 TYPE OF COORDINATE VALUES (NTYCOO) : REEL1MOT MAX DIFFERENCE +1 BETWEEN 2 NODES OF AN ELEMENT : 49 NUMBER OF COARSE ELEMENTS (NBEGM ) : 0 NUMBER OF WORDS IN ARRAY NOP5 (LNOP5 ) : 25720 REFERENCE AXIS X,Y,Z (NTACOO) : 1 &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&& END OF MODULE GEL3D1 &&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
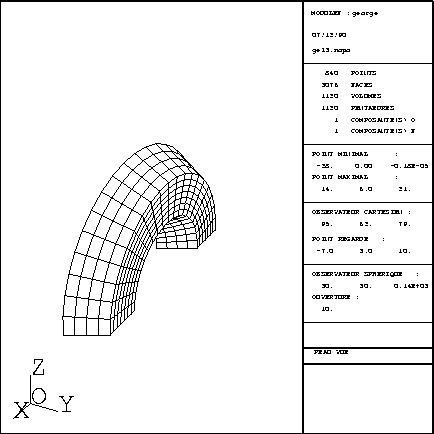
Figure 3.33: Third example of a mesh generated by GEL3D1