Next: 5.3.2 Construction of a three-dimensional mesh Up: 5.3 A three-dimensional example Prev: 5.3 A three-dimensional example Index Contents

5.3.1 Top-down analysis and mesh of the starting section

 
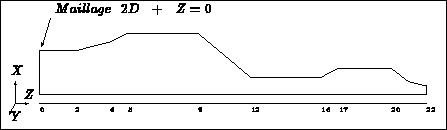
Figure 5.4: Explanatory cut through the geometry 

The domain is, topologically speaking, a cylinder. Consequently, the mesh data of one of the sections is sufficient for the construction of the 3D mesh sought.

Figure 5.4 shows a semi-cut in the symmetry plane of the domain. It allows us to see how we should define the progression of the 2D mesh and indicates how to define the different sections. We thus have successively:

• the basis: 2D mesh with side z set to 0;
• sections 0 to 2: translation of the basis via the vector (0.,0.,2.5);
• sections 2 to 4: equidistributed interpolation between section 2, already created, and section 4 defined currently as the image of the 2D mesh via function XYZ23;
• sections 4 to 5: section 5 is defined as the dilation of section 4;
• sections 5 to 9: translation of section 5 of vector (0.,0.,4.) coupled with a rotation of 5 degrees around the z-axis;
• creation of array ZINT of length 23;
• completion of this array for indices 10 to 12;
• sections 9 to 12: interpolation governed by the side (array above) between section 9 already created and section 12 defined currently as the image of the 2D mesh via function XYZ23;
• sections 12 to 16: these sections are defined as the image of the 2D mesh via function XYZ23;
• sections 16 to 17: section 17 is defined as the dilation of section 16;
• sections 17 to 20: these sections are defined, step by step, via function XYZ33;
• sections 20 to 22: section 21 is defined as the dilation of section 20, section 22 is the dilation of section 21;

The data is used to create the 2D mesh of a representative section (via module APNOPO and its preprocessor APNOXX). The mesh obtained is shown in figure 5.5.

'TEST_1_MA2D3D                                                       '
 COURBES
     1                                 $ IMPRE
 COURBE01(X,Y)=
       X*X+Y*Y-4.;                                                     
 COURBE02(X,Y)=
       X*X+Y*Y-25.;                                                    
FIN
'POINTS                                                              '
     1     5                            $ IMPRE NPOINT  $
$   NOP   NOREF(NOP)     X(NOP).            Y(NOP).  $
     1       1         -.200000E+01     0.000000E+00
     2       1         0.200000E+01     0.000000E+00
     3       2         0.500000E+01     0.000000E+00
     4       2         -.500000E+01     0.000000E+00
     5       0         0.000000E+00     0.000000E+00
'LIGNES                                                              '
     1     4                            $ IMPRE  NDLM   $
$   NOLIG NOELIG NEXTR1 NEXTR2 NOREFL NFFRON       RAISON $
       1      7      2      1      1     -3     0.100000E+01 
       5                                $ NOCE
       2      4      2      3      0      0     0.100000E+01
       3      7      3      4      2     -3     0.100000E+01
       5                                $ NOCE
       4      4      4      1      0      0     0.100000E+01
'QUAC                                                                '
     1     0     1     4    -1          $ IMPRE NIVEAU NUDSD NBRELI NS1L
 $ LIST OF CONTOUR LINES :
     1     2     3     4
     7     1                            $ IMAX NQUAD
'SYMD                                                                '
     1     0     2                      $ IMPRE NIVEA1 NIVEA2 
     0     0                            $ NBNNF NBNNSD
  0.00000E+00  0.10000E+01  0.00000E+00 $ A. B. C.
'RECO                                                                '
    1    0    2    1  0.10000E-02    1  $ IMP NIV1 NIV2 NIV3 EPS IOPT
     0     0                            $ NBNNF NBNNSD
'SAUV                                                                '
     1     1     0                      $ IMPRE NINOPO NTNOPO
 rocket2d.nopo                          
 $ FILE NAME
'FIN                                                                 '

 
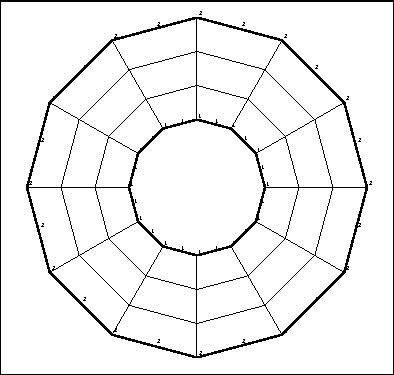
Figure 5.5: The 2D starting mesh