Next: 3.4.2 Description of the input data Up: 3.4 Method for a hexahedral topology Prev: 3.4 Method for a hexahedral topology Index Contents

3.4.1 Quick description of the method

Adapted to cubic type geometries, this method   leads to the mesh of the domain in hexahedra (which could be split subsequently) from the point data in three directions.

By being placed in the plane defined by the two first directions, a mesh is constructed. It consists of quadrilaterals whose vertices are deduced by "multiplying" the two sets of points associated to the directions. Each element of this mesh serves to construct a stacking of hexahedra by "multiplication" with the points in the third direction (figure 3.27).

 
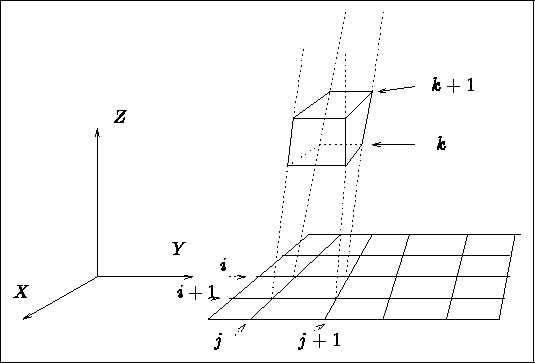
Figure 3.27: 2D partitioning and associated 3D construction 

Relatively simple in principle, this method is used to solve the mesh problem of rather complex domains entering in the frameworks of this particular topology. The connectivity is of finite difference type (i, j, k) and the position of the vertices is defined via the points given in the three privileged directions.

This technique produces essentially hexahedra. The latter can in turn be split into two pentahedra or five or six tetrahedra (see below).