Next: 4.3 Mesh modification modules Up: 4 List of the modules Prev: 4.1 Introduction Index Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Next: 4.3 Mesh modification modules
Up: 4 List of the modules
Prev: 4.1 Introduction
Index
Contents
An alphabetic list of the mesh generation modules is given below:
If the given mesh consists of triangles and quadrilaterals in R³, the mesh generator creates the mesh of the corresponding surface.
This module can be employed as an interface for non-MODULEF meshes in order to make them compatible with the modules in this code after conversion into NOPO.
Dimension array M (in the blank common), call INITI
CALL CONOPO (M,M,NDIM,NE,NP,IADEX,IAREFS,IAREFA,
. IAREFF,IACOOR,NFNOPS,NINOPS)
where
The user must address and complete the descriptive arrays in M, their addresses being passed as arguments of the module.
The arrays to complete are the following:
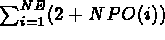 . This array contains:
. This array contains:
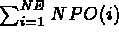 . This array contains:
. This array contains:
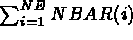 where NBAR(i) is the number of edges of element
i. This array contains:
where NBAR(i) is the number of edges of element
i. This array contains:
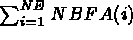 where NBFA(i) is the number of faces of element
i. This array contains:
where NBFA(i) is the number of faces of element
i. This array contains:
X(1), Y(1), X(2), Y(2), ... X(NP), Y(NP)
X(1), Y(1), Z(1), X(2), Y(2), Z(2), ... X(NP), Y(NP), Z(NP)
if NDIM = 3
The order of the vertices, edges and faces is the standard order
(see
[3] figure 4.1).
The module MAOBJE is a simplified version of CONOPO with NE=1.
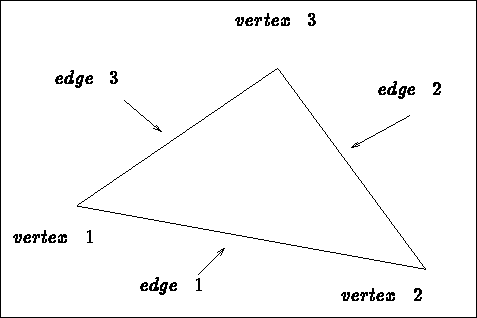
Figure 4.1: Local (ordered) numbering of the items
The only constraint is that the number of points present on 2 opposite sides must be equal.
The only constraint is that the number of points present on the 3 sides must be equal.
Dimension array M (in the blank common), declare the logical FONINT, call INITI
CALL TN2D3D (M,NFNOPE,NINOPE,NFNOPS,NINOPS,NTNOPS,
. FONINT,F2D3D,NTRANS)
where
 3D ;
3D ;  2D ;
2: mesh 1D
2D ;
2: mesh 1D  2D ;
2D ;
If NTNOPS > 0, it is necessary to input the associated arrays (see RECOLC).
Subroutine F2D3D is defined as follows:
SUBROUTINE F2D3D (X,Y,X3,Y3,Z3)
where
Modules COLIB2 and MA2D3D can also be used to construct surfaces from different data.
tn22.psfig:tn2d3dInitial meshtn23.psfig:tn2d3d1Derived surface
The contour may contain several connected components. In addition, internal points can be fixed.
The contour may contain several connected components. In addition, internal points can be fixed.