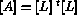 :
:
- matrix in core: module CHOLPC
- matrix out of core: module CHOLPS
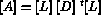 :
:
- module CROUPC
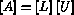 :
:
- module DRGAPC
The main advantages of a modular code are reliability, simplicity and, most important, modifiability. The latter is a crucial aspect of the MODULEF code as mathematical operators can frequently be solved by several different methods, each corresponding to a different module. With MODULEF, the user generally only needs to modify the name of the module, leaving the arguments the same, when choosing a different method. Furthermore, new numerical methods can easily be incorporated into the library. For example, the following modules correspond to different direct methods for matrix factorisation:
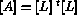 :
:
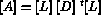 :
:
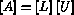 :
:
All the modules above have the same list of arguments.
Moreover, thanks to the modularity of the code, it is possible to execute modules either with single or double precision.
The data structure management and the numerical algorithm are distinct in each module.
The algorithm is confined to a standard Fortran subroutine which only accesses those arrays necessary, without referencing the dynamic storage. This enables us:
The user should have the possibility to enter the data in a simple fashion at all these levels, hence the notion free format.