Suiv.: 1.3 Mise en oeuvre dans Modulef Sup.: Généralités Préc.: 1.1 Introduction Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 1.3 Mise en oeuvre dans Modulef
Sup.: Généralités
Préc.: 1.1 Introduction
Index
Table des matières
Problème thermique :
avec :
 : flux de température au point considéré le
long d'une ligne (surface en 3D) de normale n à chaque instant t,
: flux de température au point considéré le
long d'une ligne (surface en 3D) de normale n à chaque instant t,
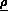 : capacité thermique,
: capacité thermique,
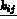 : coefficients du tenseur de conductivité thermique,
: coefficients du tenseur de conductivité thermique,
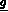 : coefficient de transfert à travers
: coefficient de transfert à travers  ,
,
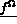 : la quantité de chaleur fournie en chaque point du domaine
: la quantité de chaleur fournie en chaque point du domaine 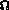 ,
,
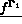 :
:  avec
avec 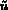 température sur
température sur 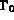 ,
,
 : température imposée sur la frontière
: température imposée sur la frontière 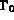 ,
,
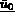 : température initiale (à l'instant
: température initiale (à l'instant 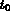 ),
),

Problème élastique (sans contraintes initiales) :
avec
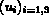 : le déplacement, à chaque instant t du point courant,
: le déplacement, à chaque instant t du point courant,
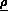 : la densité du matériau,
: la densité du matériau,
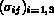 : le tenseur des contraintes,
: le tenseur des contraintes,
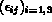 : le tenseur des déformations linéaires,
: le tenseur des déformations linéaires,
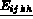 : le tenseur d'élasticité,
: le tenseur d'élasticité,
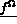 : les efforts volumiques (ou surfaciques en 2D) appliqués à
: les efforts volumiques (ou surfaciques en 2D) appliqués à 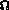 ,
,
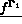 : les efforts surfaciques (ou linéiques en 2D) appliqués sur
: les efforts surfaciques (ou linéiques en 2D) appliqués sur  ,
,
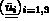 : le déplacement imposé sur
: le déplacement imposé sur 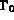 .
.
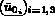 : la condition initiale (à l'instant
: la condition initiale (à l'instant 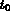 .
.
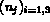 : la normale unitaire extérieure à
: la normale unitaire extérieure à  .
.
Remarque : Lorsque le matériau utilisé est isotrope, le tenseur d'élasticité et le tenseur des contraintes s'écrivent :
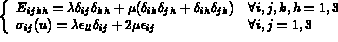
 et
et  sont les coefficients de Lamé.
sont les coefficients de Lamé.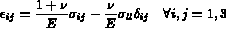
où E est le module d'Young et  le coefficient de Poisson.
le coefficient de Poisson.
Le
module d'Young E et le coefficient de Poisson  sont reliés aux coefficients de Lamé
sont reliés aux coefficients de Lamé  et
et  par les relations :
par les relations :
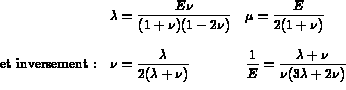
Pour ces deux exemples, toutes les données à fournir lors la résolution du problème ont été soulignées.
Sous certaines conditions de régularité, les formulations variationnelles 1.3 et 1.4 données ci-dessous sont équivalentes aux problèmes 1.1 et 1.2.
On note que les données du problème peuvent être réparties en deux classes :
Formulation variationnelle en température du problème thermique
Formulation variationnelle en déplacement du problème élastique
Au vu de ces formulations variationnelles, il est possible de recenser toutes les données à fournir au programme d'éléments finis. Ces données sont réparties en plusieurs classes , et chacune de ces classes correspond à une étape de calcul :