Suiv.: Elasticité bidimensionnelle Sup.: Les éléments finis élastiques Préc.: Les éléments finis élastiques Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Elasticité bidimensionnelle
Sup.: Les éléments finis élastiques
Préc.: Les éléments finis élastiques
Index
Table des matières
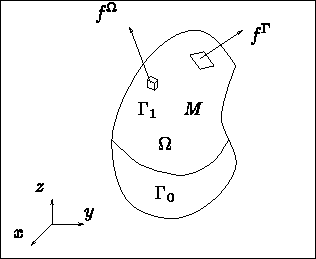
Figure: Présentation du problème
Soit  la région de
la région de 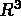 occupée par la structure dans son
état initial. On suppose que le milieu continu
occupée par la structure dans son
état initial. On suppose que le milieu continu  est soumis
à l'action de forces de volume de densité
est soumis
à l'action de forces de volume de densité 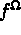 et à l'action
de forces de surfaces de densité
et à l'action
de forces de surfaces de densité 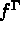 s'exerçant sur la partie
s'exerçant sur la partie 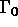 de la frontière
de la frontière 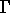 . On suppose de plus qu'une partie
. On suppose de plus qu'une partie 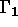 de
cette frontière est encastrée et que
de
cette frontière est encastrée et que 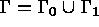 .
.
Le problème est de déterminer à tout instant t le champ des déplacements 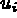 en tout point M de
en tout point M de  ainsi que le champ des contraintes
ainsi que le champ des contraintes 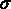 à partir de la configuration initiale donnée
à partir de la configuration initiale donnée 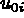 .
.
La formulation de ce problème en équations aux dérivées partielles (E.D.P.) est donnée ci-dessous.
Par la suite, la convention des indices répétés est utilisée et, 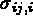 désigne
désigne 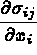 , ...
, ...
avec
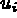 (x,y,z,t) le déplacement, à chaque instant t, du point courant (x,y,z).
(x,y,z,t) le déplacement, à chaque instant t, du point courant (x,y,z).
 la densité volumique du matériau,
la densité volumique du matériau,
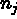 la composante j de la normale unitaire extérieure à
la composante j de la normale unitaire extérieure à 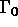 ,
,
 les efforts volumiques appliqués à
les efforts volumiques appliqués à
 et
et 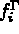 les efforts surfaciques appliqués sur
les efforts surfaciques appliqués sur 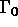 ,
,
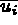 le déplacement imposé sur
le déplacement imposé sur 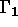 ,
,
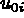 la condition initiale (t=0),
la condition initiale (t=0),
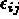 (u) le tenseur des déformations linéarisé
symétrique de Green Lagrange (hypothèses des petites déformations)
(u) le tenseur des déformations linéarisé
symétrique de Green Lagrange (hypothèses des petites déformations)
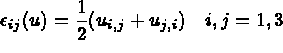
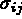 (u) le tenseur des contraintes.
(u) le tenseur des contraintes. Le tenseur des contraintes est lié au tenseur des déformations par la loi de comportement :
où  désigne le tenseur d'élasticité.
Ce tenseur vérifie les propriétés suivantes :
désigne le tenseur d'élasticité.
Ce tenseur vérifie les propriétés suivantes :
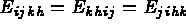
Lorsque le milieu continu est homogène isotrope, la loi de comportement (loi de Hooke) s'écrit
en fonction des coefficients de Lamé 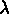 et
et  :
:

où 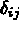 est le symbole de Kronecker.
est le symbole de Kronecker.
Les coefficients de Lamé 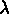 et
et  sont reliés à E le module de Young et
sont reliés à E le module de Young et  le
coefficient de Poisson par
le
coefficient de Poisson par
De plus,
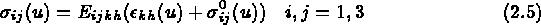
avec  les contraintes initiales
les contraintes initiales
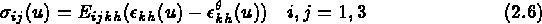
avec
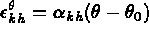
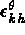 est le tenseur symétrique des
déformations thermiques
est le tenseur symétrique des
déformations thermiques
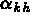 le tenseur des dilatations thermiques,
le tenseur des dilatations thermiques,
 la température à l'instant t au point (x,y,z) et,
la température à l'instant t au point (x,y,z) et,
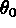 la température à l'instant t=0 au point (x,y,z).
la température à l'instant t=0 au point (x,y,z).
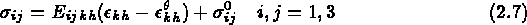
avec les mêmes notations.
Plusieurs formulations variationnelles à un ou plusieurs champs sont possibles.
C'est la formulation classique. Elle va nous permettre de fixer la terminologie et les notations.
Pour simplifier, seul le problème stationnaire est traité (le terme
 de 2.1 n'est pas considéré), et la dépendance du temps est
volontairement négligée.
La variable d'espace (x,y,z) est désignée par x.
de 2.1 n'est pas considéré), et la dépendance du temps est
volontairement négligée.
La variable d'espace (x,y,z) est désignée par x.
Le problème s'écrit comme suit :
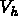 les déplacements
les déplacements 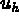 solution de :
solution de :
avec

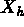 est défini par :
est défini par :
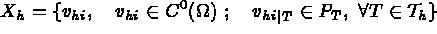
et
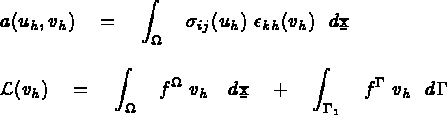
C'est à dire
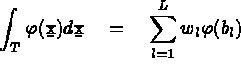
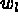 les poids de la formule d'intégration et,
les poids de la formule d'intégration et,
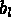 les coordonnées des points d'intégration.
les coordonnées des points d'intégration.
Alors, 2.8 est remplacée par :
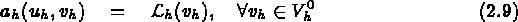
avec :
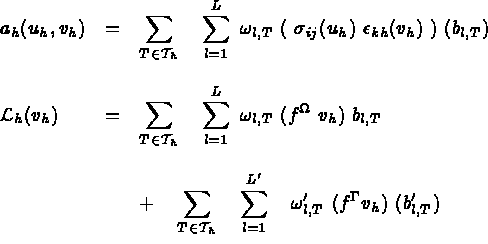
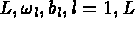 ) respectivement
(
) respectivement
(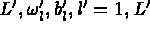 )
désigne la formule d'intégration numérique sur T et
)
désigne la formule d'intégration numérique sur T et 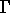 .
.
Les autres formulations variationnelles comme les formulations mixtes, les formulations hybrides primales ou bien les formulations hybrides duales ne sont pas décrites ici. Elles sont néanmoins utilisées par différents éléments finis de la bibliothèque Modulef. Pour une description détaillée de ces formulations consultez [Ciarlet], [Brezzi - Fortin] et [Roberts - Thomas].
Le but de ce paragraphe est d'indiquer la démarche suivi lors de l'implémentation d'un élément fini
pour calculer les quantités élémentaires
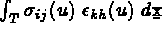 ,
,
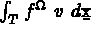 ...
...
Dans tout ce qui suit, on considère le cas d'une formulation en déplacement sans contraintes initiales et/ou couplage thermoélastique. L'indice h est également ignoré.
Le problème à résoudre s'écrit donc :

ou encore
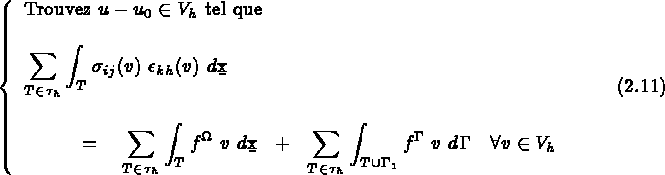
Soient  ,
, 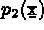 , ...,
, ..., 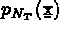 les
les  fonctions de base. On note
fonctions de base. On note
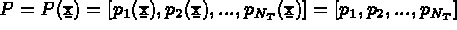
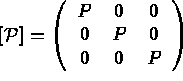
Alors,
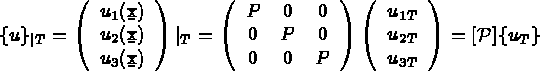
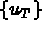 la restriction à T de { u } et
la restriction à T de { u } et 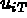 la composante i des valeurs
de la fonction u aux noeuds de l'élément T.
la composante i des valeurs
de la fonction u aux noeuds de l'élément T. Ensuite, on note
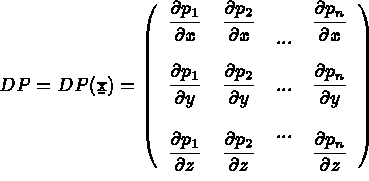
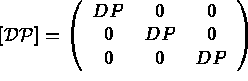
De même, on exprime 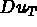 , le gradient de u, en fonction de
, le gradient de u, en fonction de
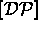 et de
et de 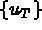 par
par
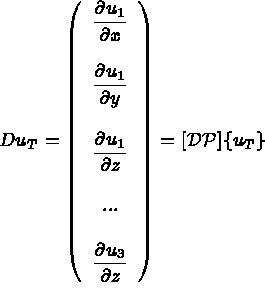
 et
et 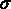 s'écrivent :
s'écrivent :
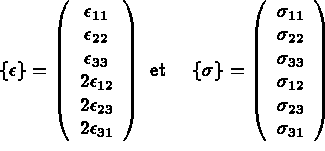
 peut être exprimé en fonction de D u
peut être exprimé en fonction de D u

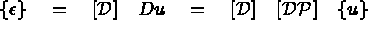
 en fonction de
en fonction de  :
:

avec pour matrice d'élasticité (donnée sous sa forme générale) :

Avec ces notations on peut écrire
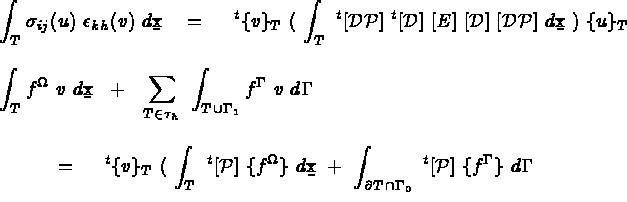
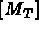 la matrice élémentaire de masse, soit
la matrice élémentaire de masse, soit
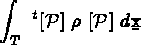
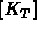 la matrice élémentaire de rigidité, soit
la matrice élémentaire de rigidité, soit
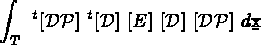
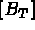 le second membre élémentaire, soit
le second membre élémentaire, soit
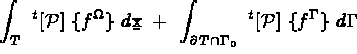
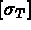 les contraintes élémentaires, soient
les contraintes élémentaires, soient
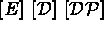
Pour obtenir le système à résoudre, il suffit de construire les matrices et seconds
membres globaux qui s'écrivent, en notant { } le vecteur des
degrés de liberté, regroupés noeuds par noeuds (et non composantes par
composantes), comme :
} le vecteur des
degrés de liberté, regroupés noeuds par noeuds (et non composantes par
composantes), comme :

avec [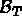 ] la matrice de permutation permettant de passer de la numérotation locale à la numérotation
globale i.e.
] la matrice de permutation permettant de passer de la numérotation locale à la numérotation
globale i.e. 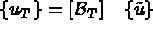 . L'opération
correspondante représente la phase d'assemblage ; elle s'écrit, dans le cas de
la matrice de rigidité par exemple, comme :
. L'opération
correspondante représente la phase d'assemblage ; elle s'écrit, dans le cas de
la matrice de rigidité par exemple, comme :
