Suiv.: Résolution par décomposition de domaines Sup.: Résolution des systèmes linéaires Préc.: Résolution par une méthode directe Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Résolution par décomposition de domaines
Sup.: Résolution des systèmes linéaires
Préc.: Résolution par une méthode directe
Index
Table des matières
Les méthodes présentées dans ce chapitre sont les méthodes classiques, de type gradient conjugué, pour la résolution d'un système linéaire. On distingue :
La première méthode est implémentée dans le code Modulef avec trois techniques de préconditionnement différentes. La matrice est stockée dans une structure de données de type AMAT.
Cette SD permet de stocker les coefficients non nuls d'une matrice creuse carrée ou rectangulaire de type "éléments finis". Ce type de stockage est appelé morse ou compact.
La SD AMAT est composée de sept tableaux dont l'organisation est prédéfinie.
Tableau AMA0 : Informations générales.
De type entier, ce tableau possède 32 variables. Il contient une description générale du travail (titre, date, nom), de la SD AMAT (type, niveau, ...) et indique la présence ou non du tableau AMA1.
le titre du travail en 20 mots de 4 caractères (stockés dans des entiers),
la date de création en 2 mots de 4 caractères (idem),
le nom du créateur en 6 mots de 4 caractères (idem),
le type de la SD,
le paramètre de niveau de la SD,
un paramètre réservé,
le nombre de tableaux supplémentaires associés à la SD
(ils seront décrits dans le tableau AMA1).
Tableau AMA1 : Descripteur des éventuels tableaux supplémentaires.
Ce tableau est analogue au tableau B1 de la SD B (voir cette SD).
Tableau AMA2 : Description générale de la matrice.
Ce tableau de type entier contient 10 valeurs.
l'ordre de la matrice,
le type des coefficients de la matrice,
le nombre de coefficients a priori non nuls de la matrice,
le nombre de mots nécessaires en mémoire centrale (M.C.) pour stocker les tableaux AMA5 et AMA6,
le nombre de pages de la matrice (si une mémoire secondaire est utilisée),
le type de stockage de la matrice avec :
le nombre de degrés de liberté par noeud s'il est constant, 0 sinon,
le nombre de noeuds,
le nombre de matrices assemblées et stockées sur la M.S. (si 0 : AMA5 existe mais AMA6 n'existe pas),
le type de la factorisation de la matrice,
0 : aucune factorisation,
1 : factorisation complète ou non de Cholesky,
2 : factorisation complète ou non de Crout,
Tableau AMA3 : Pointeur sur la dernière ligne de chaque page.
Ce tableau, de type entier et de NPAGE + 1 mots, contient :
Tableau AMA4 : Pointeur sur le coefficient diagonal de chaque ligne.
Ce tableau, de type entier et de NTDL + 1 (ou 2) mots, contient :
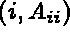 du coefficient diagonal
du coefficient diagonal  (pointe
donc sur AMA5 et AMA6)
(pointe
donc sur AMA5 et AMA6)
Tableau AMA5 : Pointeur sur les colonnes.
Ce tableau est de type entier et contient NTCOEF mots si NCODSA 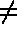 0 et 0 mots sinon :
0 et 0 mots sinon :
Tableau AMA6 : Les coefficients de la matrice.
De type NTYP, ce tableau contient les NTCOEF coefficients non nuls de la matrice :
On considère la matrice d'ordre 9 suivante (les valeurs sont les rangs dans le stockage et non les coefficients de la matrice) :

Alors, on a :
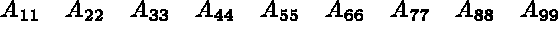
On considère la matrice d'ordre 9 suivante (les valeurs sont les rangs dans le stockage et non les coefficients de la matrice) :

Alors, on a :
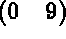
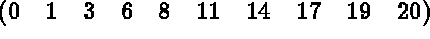

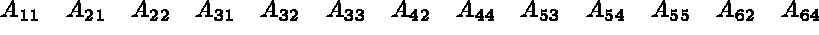
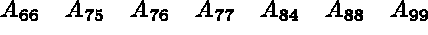
Les chaînages entre les tableaux AMA3, AMA4 et AMA5, donc la position des coefficients de la matrice dans le tableau AMA6 sont illustrés sur la figure 1.1.
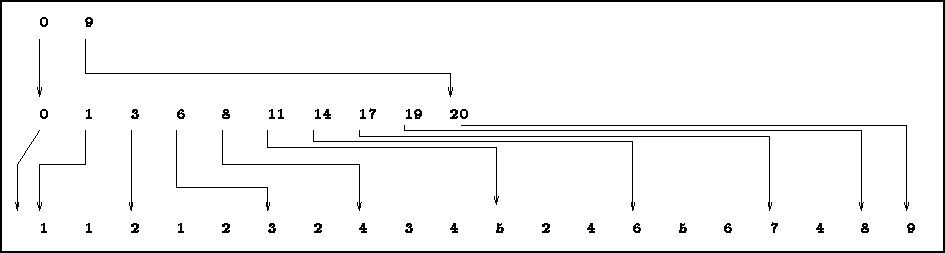
Figure: Chaînages pour l'exemple 2
On considère la matrice d'ordre 9 suivante (les valeurs sont les rangs dans le stockage et non les coefficients de la matrice) :

Alors, on a :
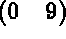

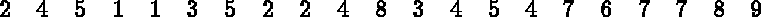
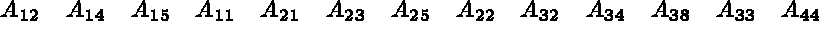

Les chaînages entre les tableaux AMA3, AMA4 et AMA5, donc la position des coefficients de la matrice dans le tableau AMA6 sont illustrés sur la figure 1.2.
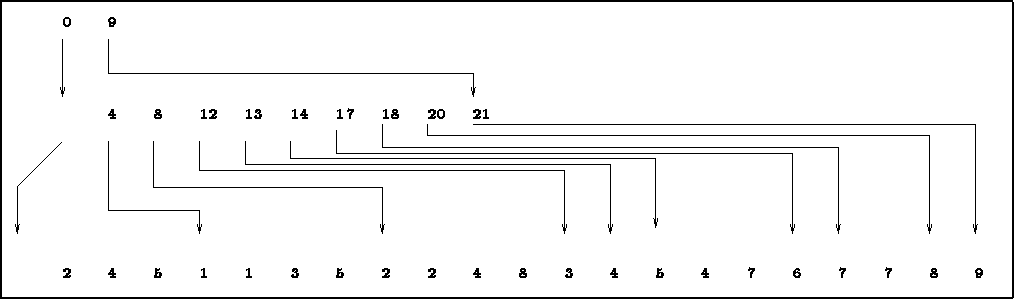
Figure: Chaînages pour l'exemple 3
Dans le cas symétrique , on stocke la matrice A
dans un tableau monodimensionnel AMAT6 de la façon suivante : pour
chaque ligne i, on ne garde que les coefficients 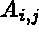 non nuls,
avec mc(i)
non nuls,
avec mc(i)  j
j  i(
i(![]() voir la description de la structure MUA
pour la définition de mc(i)), rangés
par indice de colonne j croissant. Ces lignes sont alors rangées par ordre
croissant dans AMAT6. Pour gérer la correspondance entre AMAT6 et
A, un pointeur AMAT4 est nécessaire, qui donne pour chaque ligne i
l'adresse dans AMAT6 du dernier coefficient non nul
voir la description de la structure MUA
pour la définition de mc(i)), rangés
par indice de colonne j croissant. Ces lignes sont alors rangées par ordre
croissant dans AMAT6. Pour gérer la correspondance entre AMAT6 et
A, un pointeur AMAT4 est nécessaire, qui donne pour chaque ligne i
l'adresse dans AMAT6 du dernier coefficient non nul 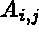 . Enfin un
pointeur AMAT5 de même taille que AMAT6, et rangé de manière
cohérente donne pour chaque coefficient
. Enfin un
pointeur AMAT5 de même taille que AMAT6, et rangé de manière
cohérente donne pour chaque coefficient 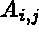 l'indice de colonne j
correspondant. On ne stocke ainsi que les coefficients non nuls de la matrice
A. L'adresse ia dans AMAT6 d'un coefficient quelconque
l'indice de colonne j
correspondant. On ne stocke ainsi que les coefficients non nuls de la matrice
A. L'adresse ia dans AMAT6 d'un coefficient quelconque 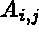 n'est
pas accessible directement, et il faut rechercher l'indice de colonne j dans
AMAT5 entre les adresses AMAT4(i)+1 et AMAT4(i+1).
n'est
pas accessible directement, et il faut rechercher l'indice de colonne j dans
AMAT5 entre les adresses AMAT4(i)+1 et AMAT4(i+1).
Dans le cas non symétrique , on adopte la même forme de stockage, c'est-à-dire que l'on garde tous les coefficients non nuls de la ligne complète, en les rangeant par indice de colonne croissant, à l'exception du coefficient diagonal, placé en bout de ligne.
Ce mode de stockage est appelé stockage compact , dans Modulef il est aussi désigné sous le nom de stockage morse .