Suiv.: Cas axisymétrique Sup.: Elasticité bidimensionnelle Préc.: 2.2 Formulation variationnelle Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Cas axisymétrique
Sup.: Elasticité bidimensionnelle
Préc.: 2.2 Formulation variationnelle
Index
Table des matières
Le but de ce paragraphe est d'indiquer la démarche suivie lors de l'implémentation d'un élément fini
pour calculer les quantités élémentaires
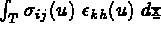 ,
,
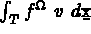 ...
...
Le passage aux quantités élémentaires est identique au cas de la dimension 3 (cf paragraphe 1.3).
Dans tout ce qui suit, on considère le cas d'une formulation en déplacement sans contraintes initiales et/ou couplage thermoélastique. L'indice h est également ignoré. La variable d'espace (x,y) est désignée par x.
Le problème à résoudre s'écrit donc :
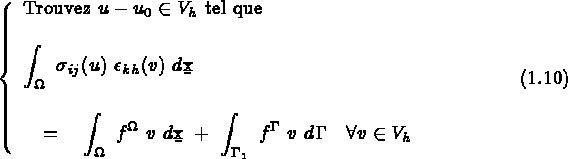
ou encore

Soient 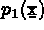 ,
, 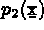 , ...,
, ...,  les
les 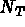 fonctions de base. On note
fonctions de base. On note

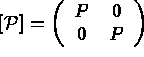
Alors,
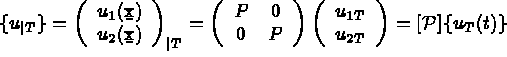
 la restriction à T de { u } et
la restriction à T de { u } et 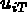 la composante i des valeurs
de la fonction u aux noeuds de l'élément T.
la composante i des valeurs
de la fonction u aux noeuds de l'élément T. Ensuite, on note
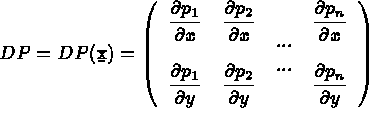
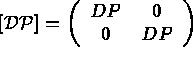
De même, on exprime 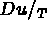 en fonction de
en fonction de  et de
et de 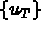 par
par
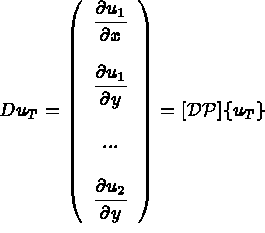
 puis
puis  s'écrivent
s'écrivent
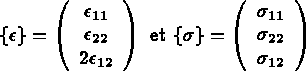
 peut être exprimé en fonction de D u
peut être exprimé en fonction de D u
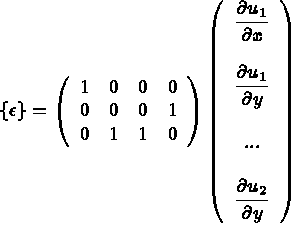
On note [ D] la matrice ci-dessus, ainsi

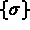 en fonction de
en fonction de  :
:

avec pour matrice d'élasticité (donnée sous sa forme générale) :
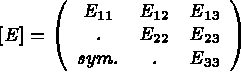
Avec ces notations on peut calculer sur chaque élément T :
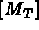 la matrice élémentaire de masse,
la matrice élémentaire de masse,
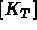 la matrice élémentaire de rigidité,
la matrice élémentaire de rigidité,
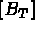 le second membre élémentaire et
le second membre élémentaire et
 les contraintes élémentaires
les contraintes élémentaires
Pour obtenir le système à résoudre, il suffit de construire les matrices et seconds membres globaux (voir également le cas de la dimension 3 paragraphe 1.4).