Suiv.: hexa3q2d Sup.: 9 Fiches techniques Préc.: tetr3p2c Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: hexa3q2d
Sup.: 9 Fiches techniques
Préc.: tetr3p2c
Index
Table des matières
DESCRIPTION DE L'ELEMENT
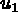 ,
, 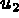 ,
, 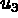 les déplacements
suivant x, y, z
les déplacements
suivant x, y, z
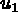 ,
, 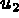 ,
, 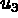
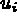 (noeud) = valeur,
(noeud) = valeur,
 (noeud) = valeur
(noeud) = valeur
Coordonnées sur l'élément de référence:
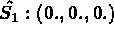
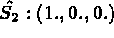
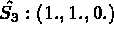
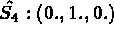
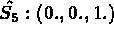
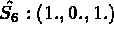
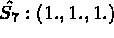
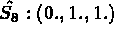
INTEGRATION NUMERIQUE
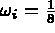 pour i=1,npiv
pour i=1,npiv
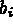 pour i=1,4 comme ci-dessous avec
pour i=1,4 comme ci-dessous avec 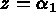
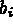 pour i=4,8 comme ci-dessous avec
pour i=4,8 comme ci-dessous avec 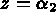
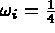 pour i=1,npis
pour i=1,npis
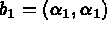 ,
,
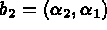 ,
,
 ,
,
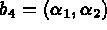
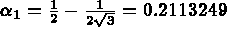 et
et
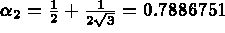
LES DONNEES A FOURNIR (en double précision)
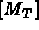 , partie
, partie 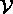
 la masse volumique supposée constante par élément.
la masse volumique supposée constante par élément.
 , partie
, partie 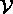
le paramètre NOTEL permet de spécifier la nature du problème:

E,
E,
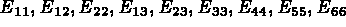
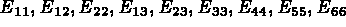
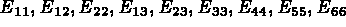
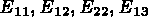 à
à 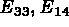 à
à 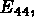 etc
etc
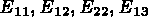 à
à 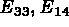 à
à 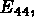 etc
etc
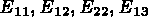 à
à 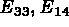 à
à 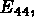 etc
etc
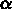 est à fournir en plus.
est à fournir en plus.
 s'il est calculé, rien sinon
s'il est calculé, rien sinon
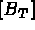 , partie
, partie 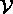
 pour i=1,NDSM; j=1,3; k=1,npiv;
la composante j du cas de charge i au point
d'intégration k .
pour i=1,NDSM; j=1,3; k=1,npiv;
la composante j du cas de charge i au point
d'intégration k .
 pour i=1,NDSM; j=1,3; k=1,npiv;
la composante j du cas de charge i au point
d'intégration k (pour partie réelle ).
pour i=1,NDSM; j=1,3; k=1,npiv;
la composante j du cas de charge i au point
d'intégration k (pour partie réelle ).
 pour i=1,NDSM; j=1,3; k=1,npiv;
la composante j du cas de charge i au point
d'intégration k (pour partie imaginaire) .
pour i=1,NDSM; j=1,3; k=1,npiv;
la composante j du cas de charge i au point
d'intégration k (pour partie imaginaire) .
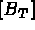 , partie
, partie 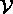
 (i,j) pour i=1,NDSM;j=1,6;la composante j (
(i,j) pour i=1,NDSM;j=1,6;la composante j ( 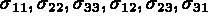 )
du cas de charge i .
)
du cas de charge i .
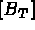 , partie
, partie 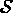
 pour i=1,NDSM; j=1,3; k=1,npis; la composante j
du cas de charge i au point
d'intégration k de la face.
pour i=1,NDSM; j=1,3; k=1,npis; la composante j
du cas de charge i au point
d'intégration k de la face.
 pour i=1,NDSM; j=1,3; k=1,npis; la composante j
du cas de charge i au point
d'intégration k de la face (pour partie réelle ).
pour i=1,NDSM; j=1,3; k=1,npis; la composante j
du cas de charge i au point
d'intégration k de la face (pour partie réelle ).
 pour i=1,NDSM; j=1,3; k=1,npis; la composante j
du cas de charge i au point
d'intégration k de la face (pour partie imaginaire) .
pour i=1,NDSM; j=1,3; k=1,npis; la composante j
du cas de charge i au point
d'intégration k de la face (pour partie imaginaire) .
Remarques
 les poids en volume (8 valeurs)
les poids en volume (8 valeurs)
 les poids en surface (4 valeurs)
les poids en surface (4 valeurs)