Next: 1.3 Solution by an iterative method Up: 1 Solution of linear systems Prev: 1.1 Introduction Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Next: 1.3 Solution by an iterative method
Up: 1 Solution of linear systems
Prev: 1.1 Introduction
Contents
The methods presented in this chapter are the three classical solution methods for a linear system by matrix factorization . We can therefore distinguish between:
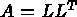 , where
L is the lower triangular matrix.
, where
L is the lower triangular matrix.
 , where L is the lower triangular matrix with unit diagonal, and D is the diagonal matrix.
, where L is the lower triangular matrix with unit diagonal, and D is the diagonal matrix.
Several versions of these three methods are implemented in the MODULEF code, according to the memory space necessary to store matrix A.
To start with, we assume that matrix A can be stored entirely in main memory, so that the storage of the matrix and the right-hand-side vector can be described exactly.
For more details consult [MODULEF User Guide - 2].
This DS stores, for each line, the coefficients lying between the first column with a a priori non-zero coefficient and the diagonal of a sparse finite element matrix. This type of storage is called profile or skyline storage.
DS MUA consists of 6 arrays of predefined order.
This integer array contains 32 variables, consisting of a general description of the job (title, date, name), of DS MUA (type, level, ...), and indicates the presence or absence of array MUA1.
the job title in 20 words of 4 characters,
the date of creation in 2 words of 4 characters,
the creator's name in 6 words of 4 characters,
the DS type,
the DS level,
a reserved parameter,
the number of supplementary arrays associated with the DS (they are described in array MUA1).
This array is analogous to array B1 of DS B (see this DS).
This integer array contains 12 values.
the type of matrix coefficients,
the number of blocks or pages in the matrix,
the number of columns of the largest block,
the number of words required in main memory to store the largest block,
the number of matrices on file,
the type of matrix storage:
the largest difference + 1 between the 2 node numbers in the same element if NCODSA is non-zero, 1 if NCODSA=0 i.e. the half band-width in terms of nodes,
the largest difference + 1 between the degree of freedom numbers of 2 nodes belonging to the same element if NCODSA is non-zero, 1 if NCODSA=0 i.e. the half band-width in terms of degrees of freedom,
the number of degrees of freedom per node if it is constant, 0 otherwise,
the number of nodes,
the matrix order,
the assembly is already performed if 1,
the assembly is not yet performed if 0.
This integer array , of length NBLOC+1, contains:
This integer array, of length NTDL+1 or 2 depending on NCODSA, contains:
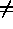 0
0
This NTYP type array contains the matrix coefficients:
Consider the 12-th order matrix given below (the values correspond to the the rows in the storage and not to the matrix coefficients) constituting 3 pages:

Array MUA5, of length MUA4(13), is subdivided into 3 pages, line 1 to 5, 6 to 10 and 11 to 12. Each page contains a maximum of 32 words. Thus, we have:
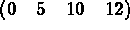
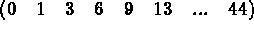
Consider the 12-th order matrix given below (the values correspond to the the rows in the storage and not to the matrix coefficients) constituting 3 pages:
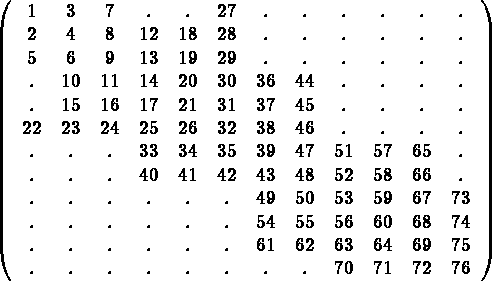
Here, each page contains a maximum of 12 words. Thus, we have:
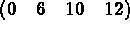

For the symmetric case we store the lower triangular part of matrix A in a one-dimensional array
MUA5 ,
as follows: for each variable i,we store all the coefficients  of the row, for
of the row, for  , (where mc(i) is
the smallest column index such that
, (where mc(i) is
the smallest column index such that 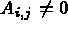 ). These coefficients (zero or not)
are ordered by increasing column index. The rows are then ordered in order of increasing variable in array MUA5.
To maintain the correspondence between MUA5 and A, a pointer MUA4 is used which gives the address of the diagonal coefficient
). These coefficients (zero or not)
are ordered by increasing column index. The rows are then ordered in order of increasing variable in array MUA5.
To maintain the correspondence between MUA5 and A, a pointer MUA4 is used which gives the address of the diagonal coefficient
 in MUA5 for each row i.
The address ia in MUA5 of an arbitrary coefficient
in MUA5 for each row i.
The address ia in MUA5 of an arbitrary coefficient  is therefore calculated by the formula
(
is therefore calculated by the formula
(![]() With the convention MUA4(1)=0)
With the convention MUA4(1)=0)
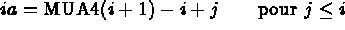
This storage mode, called profile or skyline storage, is particularly useful as it is also used for matrix L. In fact, the matrices A and L have the same profile, and in practice they are often stored in the same array).
For the non-symmetric case , the same storage is used by adding the columns in the following manner:
for each variable i, we store all the
coefficients  of the row, for
of the row, for 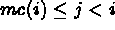 , (where mc(i) is the
smallest column index such that
, (where mc(i) is the
smallest column index such that 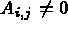 ). These coefficients (zero or not)
are ordered by increasing column index; then we store all the
coefficients
). These coefficients (zero or not)
are ordered by increasing column index; then we store all the
coefficients  of the column, for
of the column, for  ,
ending with the diagonal coefficient. This information is then ordered
in order of increasing variable in array
MUA5.
To maintain the correspondence between MUA5 and A, a pointer MUA4 is used which gives the address of the diagonal coefficient
,
ending with the diagonal coefficient. This information is then ordered
in order of increasing variable in array
MUA5.
To maintain the correspondence between MUA5 and A, a pointer MUA4 is used which gives the address of the diagonal coefficient
 in MUA5 for each row i.
The address ia in MUA5 of an arbitrary coefficient
in MUA5 for each row i.
The address ia in MUA5 of an arbitrary coefficient  is therefore calculated by the formula
is therefore calculated by the formula

For more details consult [MODULEF User Guide - 2].
This DS stores a coefficient array in the form of a vector (right-hand-side (RHS) of a system, solution, etc.).
In practice, matrix B has the form B(NDSM,NTDL) where NDSM designates, for example, the number of load cases of RHS and NTDL is the number of degrees of freedom.
DS B consists of five arrays of predefined order.
This integer array contains 32 variables, consisting of a general description of the job (title, date, name), of DS B (type, level, ...), and indicates the presence or absence of array B1.
the job title in 20 words of 4 characters,
the date of creation in 2 words of 4 characters,
the creator's name in 6 words of 4 characters,
the DS type,
the DS level,
a reserved parameter,
the number of supplementary arrays associated with the DS (they are described in array B1).
This integer array exists if NTACM (see B0) is non-zero. It contains, for each array to be described, 22 variables. In general, there are no associated arrays, except for certain applications where it is necessary to store values in the DS which do not enter its standard definition.
If array B1 exists, it contains sequentially:
This integer array contains 11 values.
the type of array B4,
the number of indices (fixed to 2),
the maximum value of its first index (for example, NDSM, the number of load cases),
the maximum value of its second index (for example, NTDL if B4 only has one page),
the code for splitting array B4 into blocks, with:
the number of blocks,
the number of nodes,
the number of B4 arrays when the DS is on file,
the number of degrees of freedom per node if it is constant, or 0,
the number of degrees of freedom or the maximum value of the second index of array B4 when the NBLOC blocks are considered,
the storage code for array B4 with:
This integer array contains NBLOC+1 variables indicating the segmentation of array B4.
This NTYP type array contains the NDSM*M2 values of each page.
This set of 5 arrays (B0, B1, B2, B3 and B4) managed by a few subroutines, contain the NDSM right-hand-sides (or solutions) of the linear system A x = b. The coefficients of array B4(NDSM,NTDL) represent the NTDL components of the NDSM right-hand-sides of the linear system to be solved. After the solution procedure, the solutions of the linear system are also stored in array B4 (the same, or one of a distinct structure B).