Suiv.: 2.2 Les modules COMAC2COMAC3 et Sup.: 2 Interpolation Préc.: 2 Interpolation Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 2.2 Les modules COMAC2COMAC3 et
Sup.: 2 Interpolation
Préc.: 2 Interpolation
Index
Table des matières
Dans la bibliothèque Modulef, l'étape d'interpolation consiste en :
Nous donnons maintenant quelques informations sur chacune de ces trois étapes, ainsi que quelques principes généraux sur l'utilisation des modules d'interpolation.
Le type de problème à résoudre est donné par l'intermédiaire du nom de la bibliothèque ( NOMBIB) et du nom du ou des éléments finis utilisés (tableau ICODEL). Deux possibilités se présentent,
La formulation variationnelle d'un problème nous donne les inconnues variationnelles ou fonctionnelles de ce problème continu (par opposition au problème discret).
Chacune des inconnues variationnelles est, par définition de la méthode des éléments finis, interpolée sur tout ou une partie d'un élément par une fonction simple, généralement un polynôme, qui fait partie d'un espace vectoriel de dimension finie. Un choix de base particulièrement intéressant fait intervenir comme coefficient, la valeur de l'inconnue, de ses dérivées ou ..., en certains noeuds de l'élément.
La connaissance des inconnues en chaque noeuds de l'élément entraîne celle de la solution sur tout l'élément. Ces valeurs discrètes une fois regroupées pour tous les éléments qui recouvrent le domaine, constituent les inconnues du système linéaire global. L'étude des structures mécaniques ayant été la source de la méthode des éléments finis, Zienkiewicz a nommé une telle inconnue degré de liberté généralisé .
La signification d'un degré de liberté (en abrégé d.l.) peut être diverse. Afin de fournir des résultats clairs, un mnémonique , repéré par un numéro de code, est associé à chacun d'eux :
Généralement, le d.l. exprime une valeur de l'inconnue variationnelle ou de ses dérivées en un point. Ce point qui supporte les degrés de liberté d'au moins une inconnue variationnelle sera appelé désormais un noeud .
Un noeud peut supporter un ou plusieurs d.l. de une
ou plusieurs inconnues variationnelles et, pour une inconnue existe une
hiérarchie.
Exemple 1 :
| inconnue variationnelle 1 | : | VN |
| DX | ||
| DY | ||
| DZ | ||
| inconnue variationnelle 2 | : | VN |
| DN |
Les numéros locaux des d.l. de ce noeud sont respectivement 1, 2, 3, 4, 5, 6.
Un élément fini comprend plusieurs noeuds (sauf s'il simule un ressort).
La numérotation locale des noeuds de l'élément est, quant à elle, fixée suivant la probabilité de plus grande utilisation c'est-à-dire :
La numérotation locale de l'ensemble des d.l. des noeuds d'un
élément se déduit de celle des noeuds :
les d.l. du premier noeud d'abord, ceux du second ensuite ...
Exemple 2 :
|
|
|
soit une interpolation
| numéro du d.l. | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
| noeud | 1 | 2 | ||||||
| mnémonique | VN(1) | DX(1) | DY(1) | VN(2) | VN(1) | DX(1) | DY(1) | VN(2) |
| numéro de d.l. | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
| noeud | 3 | 4 | 5 | 6 | 7 | |||
| mnémonique | VN(1) | DX(1) | DY(1) | VN(2) | VN(2) | VN(2) | VN(2) | VN(1) |
où VN(i) désigne la valeur au noeud de la i-ème inconnue variationnelle.
Un maillage comprend de nombreux éléments. Certains noeuds sont communs à plusieurs éléments. Par suite, les d.l. de ces noeuds sont généralement communs à ces éléments.
Exemple 3 :
|
|
Le noeud 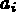 est commun aux 5 éléments mais fournit au
système global à résoudre, dans le cadre de l'exemple 2
seulement 4
d.l. : est commun aux 5 éléments mais fournit au
système global à résoudre, dans le cadre de l'exemple 2
seulement 4
d.l. :
|
Afin de décrire sans ambiguïté les noeuds d'un élément du maillage une méthode consiste à les numéroter globalement de 1 à NOE.
Un élément est topologiquement décrit par la liste de ses noeuds dans cette numérotation globale. Cette numérotation globale des noeuds induit celle, globale, des degrés de liberté, cette numérotation varie de 1 à NTDL, où NTDL est la dimension du système à résoudre.
Exemple 4 :
Si l'on reprend le même type d'interpolation que dans l'exemple 2,
la numérotation des d.l. des noeuds décrits en
figure 2.1
est donnée dans le tableau 2.1.
| Sommets | Milieux | Barycentre | ||||||||||||||
| noeud | 1 | 10 | 12 | 2 | 11 | 3 | 13 | |||||||||
| n°d.l. | 1 | 2 | 3 | 4 | 30 | 31 | 32 | 33 | 35 | 36 | 37 | 38 | 5 | 34 | 6 | 44 |
Table: Numérotation des degrés de liberté des noeuds
Comment s'y retrouver parmi toutes ces numérotations ?
Exemple :
Soit un domaine recouvert par des triangles de type identique à ceux
défini dans l'exemple 1: il est composé de trois types de
noeuds :
| Type 1 | : | les sommets | inconnue variationnelle 1 | VN |
| DX | ||||
| DY | ||||
| inconnue variationnelle 2 | VN | |||
| Type 2 | : | les milieux des côtés | inconnue variationnelle 2 | VN |
| Type 3 | : | les barycentres | inconnue variationnelle 1 | VN |
Généralement, les matrices et seconds membres associés à
un élément fini T sont calculés à partir d'un changement de
variables c'est à dire d'une transformation notée 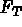 qui
envoie l'élément de référence
qui
envoie l'élément de référence 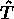 sur l'élément
réel T. Cette application est définie à partir de données
telles que les coordonnées de certains points ou les tangentes en
ces mêmes points.
sur l'élément
réel T. Cette application est définie à partir de données
telles que les coordonnées de certains points ou les tangentes en
ces mêmes points.
Nous dirons qu'un point sert à définir la
transformation 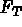 , appelée encore métrique ou géométrie
de l'élément.
, appelée encore métrique ou géométrie
de l'élément.
Il convient de se rappeler qu'un noeud est un support de degrés de liberté. Un point est défini par ses coordonnées mais aussi parfois par des directions tangentes aux arêtes courbes ... Ces autres coordonnées sont appelées caractéristiques associées au point.
Afin de les caractériser, à chacune d'elles est associé un
mnémonique qui pour simplifier les données est identique
dans sa présentation à celui des d.l. des noeuds. C'est logique
car les coordonnées et caractéristiques des points sont les
degrés de liberté de l'application 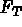 .
.
Par suite,
| VN | de numéro de code 1 | désigne les coordonnées |
| DTG | de numéro de code 5 | désigne une tangente première |
| DDTG | de numéro de code 13 | désigne une tangente seconde |
Bien entendu, à chaque mnémonique d'un point correspondent NDIM composantes donc NDIM valeurs (où NDIM est la dimension de l'espace).
Etant donné qu'il peut y avoir plusieurs tangentes au même point, leur présentation devra être synchrone avec leur utilisation. La fiche technique d'un tel élément est explicite sur ce sujet.
De façon analogue aux noeuds, un maillage comprend plusieurs points mais un faible nombre d'entre eux suffit à les caractériser, ce sont les types de points .
Les coordonnées et caractéristiques des points sont rangées dans le tableau COO4 de la S.D. COOR. Si les coordonnées d'un point sont stockées d'après le numéro global de ce point, les composantes des caractéristiques sont rangées par élément.
Les numéros des points n'ont aucune raison particulière d'être consécutif. En effet, ils servent seulement à retrouver les coordonnées dans le tableau COO4. Par suite, un point peut même avoir plusieurs numéros dont les coordonnées identiques apparaîtront plusieurs fois dans le stockage.
Ainsi, un point peut avoir plusieurs types mais, dans un élément, il n'en a qu'un seul. Comme le travail s'effectue élément par élément, il n'y a pas d'ambiguïté.
Si l'on utilise des éléments finis de la bibliothèque, par sous-domaine, les types d'éléments possibles sont :
La métrique et la topologie ont été totalement dissociées : les noeuds d'une part, les points d'autre part, la S.D. MAIL d'une part la S.D. COOR d'autre part. Ainsi le passage d'éléments droits à éléments courbes peut être effectué sans modifier les noeuds ; des perturbations d'un maillage sans dégénérescence d'éléments peuvent être gérées en ne modifiant que les valeurs du tableau COO4.
A chaque élément constituant le maillage sont associés des attributs physiques :
Un maillage, s'il comprend plusieurs dizaines, centaines ou milliers d'éléments en contient en fait un grand nombre du même type.
Si un type d'élément est totalement caractérisé et si le type de chaque élément du maillage est stocké, alors d'une part aucune ambiguïté n'est à craindre, d'autre part, le nombre d'informations à conserver pour un élément courant est minimisé et les risques d'erreurs sont réduits d'autant. Un type d'élément caractérise qualitativement un grand nombre d'éléments du maillage. Chaque type d'élément est défini lorsque sont fixées :
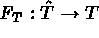
Une modification de l'un de ces termes (quelqu'il soit), conduit à la création de deux types d'éléments distincts. Les informations nécessaires pour la description d'un type d'élément sont :
Les tableaux joints à un type d'élément permettent de
stocker un grand nombre d'informations sur cet élément :
Pour chaque élément frontalier, nous stockons le numéro de
référence de ses sommets et/ou de ses arêtes et/ou de ses
faces.
Comme un noeud est soit un sommet, soit sur une arête, soit sur une
face, soit interne à l'élément, le numéro de référence
de la géométrie sur laquelle il s'appuie détermine son numéro
de référence.
Si l'élément est frontalier ou référé, le numéro de
référence de chaque noeud est immédiatement déduit, sinon,
si il est interne, aucun numéro n'est utilisé.
Ainsi on peut retrouver aisément le coefficient d'échange de telle
face, les types des conditions aux limites de telle arête ...
Il est nécessaire de décrire le nombre maximum des tableaux
qui peuvent être joints à un type d'élément mais, un
élément pourra en supporter moins. C'est le cas, par exemple, des
éléments internes pour lesquels il n'est pas nécessaire de
stocker des zéros (convention d'une position interne). C'est la
raison pour laquelle, pour chaque élément on mentionne le nombre
de tableaux à lire.
Cependant, ces tableaux absents doivent être les derniers et, par
exemple, l'avant dernier ne peut être absent si le dernier ne l'est
pas.
L'adjonction du tableau des numéros de frontières des arêtes
puis des sommets des éléments frontaliers issus de la S.D. NOPO
est automatique lors de l'exécution de COMACO (COMAC2 et COMAC3) ;
l'utilisateur n'a pas à s'en occuper.
Selon toutes ces notions et leur mode de stockage respectif, un élément courant est décrit très précisément par :
Lorsque la bibliothèque d'éléments finis est
utilisée pour définir les types d'éléments finis construits
sur le maillage, la notion d'élément courbe apparaît.
Un élément courbe est
Nous avons vu qu'il est possible de travailler avec des
éléments courbes, dans ce cas,
les points
non sommets sont obtenus par transformation de leurs
coordonnées sur l'élément de référence, projetés sur le
sous-domaine, la face ou la ligne courbe ; cette transformation est
affine pour un triangle
et pour un tétraèdre (P1), quadratique pour un quadrilatère et
un hexaèdre (Q1), mixte pour un pentaèdre. La fonction FFRONT et le
sous-programme CALFC permettent de décrire les équations des
lignes et surfaces courbes.
Nous précisons maintenant l'utilisation de ces deux sous-programmes.
Si le numéro de référence ne correspond pas à un numéro de
ligne courbe, ou si le point est interne, le numéro de référence
I du sous-domaine courbe est recherché ; si un tel numéro existe,
la projection est faite sur le sous-domaine courbe dont l'équation
est donné par le sous-programme
CALFC(I,X,Y,Z,F).
 , appartenant à deux faces,
ou de deux points identiques appartenant à deux éléments
différents, peuvent être distinctes (
, appartenant à deux faces,
ou de deux points identiques appartenant à deux éléments
différents, peuvent être distinctes ( et
et  ). Dans ce
cas, le point projeté sera le point de la surface courbe,
appartenant à la bissectrice de l'angle
(
). Dans ce
cas, le point projeté sera le point de la surface courbe,
appartenant à la bissectrice de l'angle
( ).
Lorsque l'ensemble des points de l'ensemble des éléments sont
traités, on recherche si les points stockés correspondent à des
points identiques (de même coordonnées) qui ont été
projetés. Dans ce cas, les coordonnées du point stocké sont
égales à celles de la projection.
).
Lorsque l'ensemble des points de l'ensemble des éléments sont
traités, on recherche si les points stockés correspondent à des
points identiques (de même coordonnées) qui ont été
projetés. Dans ce cas, les coordonnées du point stocké sont
égales à celles de la projection.
Définition :
Lors de l'appel de chacun des modules d'interpolation, l'utilisateur précise le nombre et le nom des éléments droits et courbes utilisés. Si deux éléments de type différent mais de même géométrie apparaissent, l'un en élément droit l'autre en élément courbe, le programme affecte
Le tableau 2.2 nous donne les différentes possibilités de répartition de ces éléments dans le domaine 2.2.
| Cas 1 | Cas 2 | Cas 3 | Cas 4 | |
| Données : | ||||
| élément droit | TRIA 2P2D | TRIA 2P2D | TRIA 2P2D | |
| élément courbe | TRIA 2P2C | TRIA 2P2C | TRIA 2P2C | |
| lignes courbes | 1 : ligne 2-3 | 0 | a) 0 | 1 : ligne 2-3 |
| b) 1 : ligne 2-3 | ||||
| Résultats : | ||||
| élément droit | 1, 2 | 1, 2, 3, 4 | données | |
| élément courbe | 3, 4 | 1, 2, 3, 4 | incohérentes | |
| (noeuds projetés) | 7, 9 | a) | ||
| b) 7, 9 | ||||
Le cas 4 est incohérent car les éléments 1 et 2 sont de type droit alors qu'aucun élément de ce type n'a été déclaré.
Table: Répartition des éléments droits et courbes
Remarque : Dès qu'un élément n'a pas un numéro de référence correspondant à une frontière courbe, il faut définir des éléments droits.
On désire discrétiser le domaine défini sur la figure 2.3,
à l'aide de l'élément fini courbe TRIA 2P2C (le nombre de lignes courbes est nul).
| Cas 1 | Cas 2 | Cas 3 | |
| élément droit | TRIA 2P2C | TRIA2P2C | |
| élément courbe | TRIA 2P2C | TRIA2P2C |
Parmi ces trois jeux de données un seul le troisième est correct. En effet, le cas 2 est faux (cf Remarque précédente) ; le cas 1 également puisque l'élément TRIA 2P2C est de type courbe et que cette caractéristique n'a pas été introduite.