Suiv.: 4.3 Le module COBDCL Sup.: Conditions aux limites Forcées Préc.: Généralités Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 4.3 Le module COBDCL
Sup.: Conditions aux limites Forcées
Préc.: Généralités
Index
Table des matières
Le but de ce module est de créer la structure de données BDCL ( Blocage Des Conditions aux Limites ).
Deux types de conditions aux limites sont admis (cf paragraphe 4.1) :
Le module COBDC1 est utilisé lorsque la valeur de blocage est :
Le fichier support de la S.D. BDCL doit être en accès séquentiel (l'accès direct n'est pas programmé).
Certaines limites d'utilisation existent lorsque l'on décrit des conditions aux limites en relation linéaire, pour plus de détails consultez le paragraphe 4.2.3


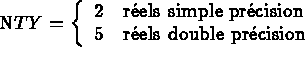
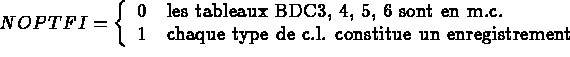

Lors d'une utilisation standard les S.D. TYNO et MPLR n'existent pas et donc, IEMAIL = 1 IETYNO = IEMPLR = 0
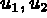 ) le
déplacement. Il y a deux inconnues variationnelles :
) le
déplacement. Il y a deux inconnues variationnelles :
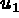 : le déplacement en x (mnémonique VN)
: le déplacement en x (mnémonique VN)
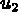 : le déplacement en y (mnémonique VN)
: le déplacement en y (mnémonique VN)
Considérons deux cas test :
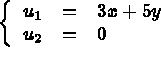
Des sous-programmes ou fonctions supplémentaires sont nécessaires lorsque : ICONST = 2 ou NCLRL = -1
REAL FUNCTION VALCLR (I, X, Y, Z)
DOUBLE PRECISION FUNCTION VALCLD (I, X, Y, Z)
COMPLEX FUNCTION VALCLC (I, X, Y, Z)
DOUBLE PRECISION FUNCTION VALCLD (I, X, Y, Z) REAL X, Y, Z INTEGER I IF (I .EQ. 1) THEN VALCLD = 3*X + 5*Y ELSE IF (I .EQ. 2) THEN VALCLD = 0 ENDIF END
SUBROUTINE SPCLRL(M, NOEFF, NOFR, NNR, NBNOE, NUNOE,
[4] COO4, NDIM, NCLRL,
NMTRL, BDC5, LB5, BDC6, LB6, EPS)
Dans le paragraphe 4.2.3 nous donnons plus de détails sur la façon de traiter les conditions aux limites en relation linéaire ainsi qu'un exemple d'utilisation du sous-programme SPCLRL.
Les fichiers contenant les S.D. d'entrée et sortie, ils ne sont pas
tous nécessaires car les S.D. peuvent rester en mémoire centrale :
NFMAIL, NFTYNO, NFMPLR, NFNDL1, NFCOOR, NFBDCL
Les bibliothèques Modulef utilisées par le module COBDC1 sont dans
l'ordre :
COSD, UTSD, ZZZZ_MOD, UTII, U_xxx(![]() utilitaires
spécifiques à une machine)
utilitaires
spécifiques à une machine)
Comme tous les modules
de création de structures de données (COMACO, COFORC, THENEW
...) le module COBDC1 donne à l'utilisateur la possibilité
d'associer NTASD tableaux à la structure qui est créée.
Si cette option est choisie, pour chaque
tableau les
informations suivantes doivent être données :
Pour I de 1 au nombre de tableaux,
 * L1 où
* L1 où
 = 1
= 1
 = 2
= 2
 = 4
= 4
Le traitement d'une relation linéaire entre plusieurs degrés de liberté du type :
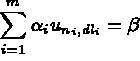
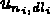 représente la valeur du
représente la valeur du
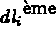 degré
de liberté du noeud
degré
de liberté du noeud 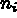
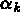 est le
est le
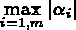 est choisi
comme pivot. Si plusieurs d.l. ont des coefficients de même
valeur absolue le premier rencontré est choisi.
est choisi
comme pivot. Si plusieurs d.l. ont des coefficients de même
valeur absolue le premier rencontré est choisi.
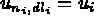 , un changement de variables
, un changement de variables
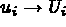 est effectué avec
est effectué avec
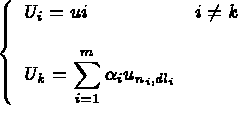
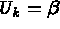
Si plusieurs relations linéaires entre coefficients apparaissent il est possible de distinguer deux cas :
Exemple : Conditions aux limites équipotentielles :
Les relations linéaires seront utilisés afin d'indiquer que la
valeur de la solution doit être constante en tous les noeuds d'une
frontière 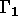 mais, la valeur de la constante n'est pas
connue.
Supposons que les noeuds sur cette frontière soient numérotés
de 1 à m.
Parmi les différentes façons de formuler le type de conditions
il y a :
mais, la valeur de la constante n'est pas
connue.
Supposons que les noeuds sur cette frontière soient numérotés
de 1 à m.
Parmi les différentes façons de formuler le type de conditions
il y a :
La formulation 4.1 est incorrecte (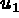 est pivot de
m-1 relations linéaires), alors que la formulation 4.2
est juste.
est pivot de
m-1 relations linéaires), alors que la formulation 4.2
est juste.
Un problème thermique contenant des conditions aux limites en relation linéaire est donné en exemple paragraphe 4.2.4.
Dans ce programme nous donnons deux exemples d'appel du module
COBDC1.
Dans le premier exemple (paragraphe 4.2.4), nous décrivons des conditions aux limites de
type Dirichlet, nous donnons dans ce cadre un exemple de
programmation de la fonction VALCLR.
Dans le second exemple (paragraphe 4.2.4), nous
décrivons des conditions en limites aux
relations linéaires (ces conditions sont de type équipotentiel),
nous donnons un exemple de programmation du sous-programme SPCLRL.
Ces deux exemples s'appuient sur le même domaine d'étude ; ce
domaine est donné figure 4.1.
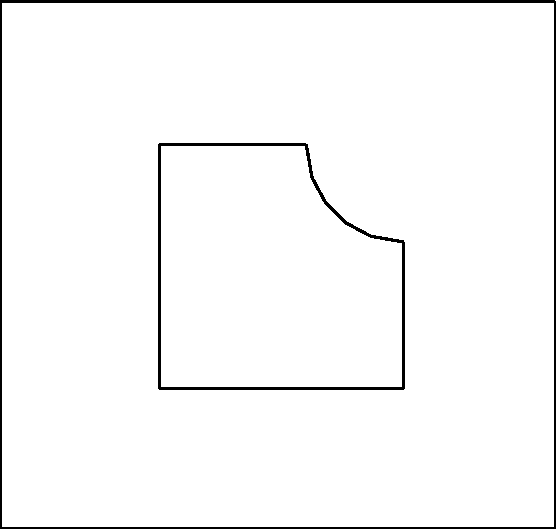
Figure: Le problème thermique bidimensionnel
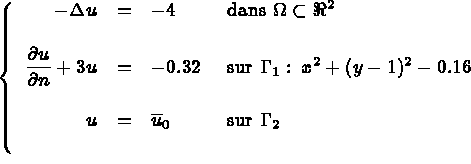
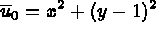
Ce problème admet une solution exacte :
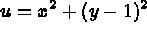
Une formulation variationnelle en température est utilisée. On choisit une interpolation de type P3 Hermite, l'élément fini correspondant est TRIA 2P3D, l'inconnue variationnelle est u la température. Il y a trois degrés de liberté de mnémonique VN, DX, DY et, les points et les noeuds coïncident. Et, les conditions aux limites forcées sont :

Le programme appelant le module COBDC1 est défini comme suit : {
1 PROGRAM T1BDCL
2 C +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
3 C BLOCAGE DES CONDITIONS AUX LIMITES - ELEMENT THER TRIA 2P3D
4 C +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
5 C S.D.E. : MAIL COOR DE NOM RESPECTIF T4MAIL ET T4COOR
6 C
7 C S.D.S. : BDCL
8 C +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
9 C
10 C PROGRAMMEUR P. PATE INRIA - SIMULOG JUIN 92
11 C
12 C ...................................................................
13 C
14 PARAMETER ( LM = 45000 )
15 COMMON M(LM)
16 DOUBLE PRECISION DM
17 EQUIVALENCE (M(1),DM)
18 C
19 INTEGER NNN, IMPRE
20 CHARACTER*80 NOMFIC
21 DIMENSION NOFR(3,3),VAL(3)
22 REAL VAL, VALCLR
23 DOUBLE PRECISION VALCLD
24 EXTERNAL VALCLR, VALCLD
25 C
26 100 FORMAT('NOM DE LA S.D.E MAIL') #F
27 110 FORMAT('NOM DE LA S.D.E COOR') #F
28 120 FORMAT('NOM DE LA S.D.S BDCL') #F
29 C100 FORMAT('NAME OF THE INPUT D.S. MAIL') #GB
30 C110 FORMAT('NAME OF THE INPUT D.S. COOR') #GB
31 C120 FORMAT('NAME OF THE OUTPUT D.S. BDCL') #GB
32 C
33 C INITIALISATION
34 C --------------
35 NNN = 0
36 IMPRE = 5
37 CALL INITIS(M,LM,IMPRE,NNN)
38 IMPRIM = IINFO('I')
39 C
40 C OUVERTURE DES FICHIERS CONTENANT LES S.D. D'ENTREE MAIL ET COOR
41 C ----------------------------------------------------------------
42 WRITE(IMPRIM,100)
43 CALL LIBCAR(NOMFIC)
44 CALL TRUNIT(NFMAIL)
45 CALL OUVRIS(NFMAIL,NOMFIC,'OLD,UNFORMATTED',0)
46 NIMAIL = 1
47 C
48 WRITE(IMPRIM,110)
49 CALL LIBCAR(NOMFIC)
50 CALL TRUNIT(NFCOOR)
51 CALL OUVRIS(NFCOOR,NOMFIC,'OLD,UNFORMATTED',0)
52 NICOOR = 1
53 C
54 C OUVERTURE DU FICHIER CONTENANT LA S.D. DE SORTIE BDCL
55 C ------------------------------------------------------
56 WRITE(IMPRIM,120)
57 CALL LIBCAR(NOMFIC)
58 CALL TRUNIT(NFBDCL)
59 CALL OUVRIS(NFBDCL,NOMFIC,'UNFORMATTED',0)
60 NIBDCL = 1
61 NTBDCL = 0
62 C
63 C S.D. NDL1
64 C ---------
65 C IL EST INUTILE DE CREER LA S.D. NDL1 CAR LE NOMBRE DE DEGRE
66 C DE LIBERTE PAR NOEUD EST CONSTANT (1)
67 C
68 NFNDL1 = 0
69 NINDL1 = 0
70 C
71 C APPEL DU MODULE COBDC1 => S.D. BDCL
72 C ----------------------
73 C LES INCONNUES BLOQUEES SONT DECRITES SOUS FORME DE TRIPLET
74 NBFR = 3
75 DO 1 I=1,3
76 NOFR(I,1) = 2
77 NOFR(I,2) = 1
78 1 CONTINUE
79 NOFR(1,3) = ICHAR4('VN ')
80 NOFR(2,3) = ICHAR4('DX ')
81 NOFR(3,3) = ICHAR4('DY ')
82 C
83 C ON TRAVAILLE EN SIMPLE PRECISION
84 NTY = 2
85 IEMAIL = 1
86 IETYNO = 0
87 NFTYNO = 0
88 NITYNO = 1
89 IEMPLR = 0
90 NFMPLR = 0
91 NIMPLR = 1
92 NOPFI = 0
93 C
94 ICONST = 2
95 C
96 NCLRL = 0
97 NMTRL = 0
98 ITA5 = 0
99 ITA6 = 0
100 C
101 FONINT = .FALSE.
102 C
103 C APPEL DE COBDC1
104 C ---------------
105 CALL COBDC1(M,ICONST,NBFR,NOFR,NTY,VAL,NCLRL,NMTRL,ITA5,ITA6,
106 + IEMAIL,NFMAIL,NIMAIL,IETYNO,NFTYNO,NITYNO,IEMPLR,NFMPLR,
107 + NIMPLR,NFNDL1,NINDL1,NFCOOR,NICOOR,NFBDCL,NIBDCL,NTBDCL,
108 + NOPFI,FONINT,VALCLR,VALCLD)
109 C
110 C IMPRESSION DE LA S.D. BDCL
111 C --------------------------
112 CALL IMBDCL(M,NFBDCL,NIBDCL,IMPRE)
113 C
114 C FERMETURE DE FICHIERS
115 C ---------------------
116 CLOSE(NFMAIL)
117 CLOSE(NFBDCL)
118 END
119 C
}
Remarques :
Puisque les points et les noeuds coïncident partout, la S.D.
d'entrée COOR du module COBDC1
est la même que celle issue du module COMACO, il est donc inutile
d'appeler le module CORNOE.
1 REAL FUNCTION VALCLR(I,X,Y,Z)
2 C +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
3 C BUT : DESCRIPTION DES CONDITIONS AUX LIMITES BLOQUEES
4 C ...................................................................
5 C PARAMETRES D'ENTREE
6 C -------------------
7 C I : NUMERO DE LA LIGNE DU TABLEAU NOFR DECRIVANT LE TRIPLET
8 C X, Y, Z : COORDONNEES DU NOEUD
9 C
10 C PARAMETRES DE SORTIE
11 C --------------------
12 C VALCLR : VALEUR DE BLOCAGE
13 C ...................................................................
14 C
15 C PROGRAMMEUR P. PATE INRIA - SIMULOG JUIN 92
16 C ...................................................................
17 INTEGER I
18 REAL X, Y, Z
19 C
20 IF ( I .EQ. 1) THEN
21 VALCLR = X*X +(Y-1)*(Y-1)
22 ELSE IF ( I .EQ. 2) THEN
23 VALCLR = 2*X
24 ELSE IF ( I .EQ. 3) THEN
25 VALCLR = 2*(Y-1)
26 ENDIF
27 END
}
Le listing d'exécution du programme t1bdcl est donné ci-dessous :
{
M M OOO DDDD U U L EEEEE FFFFF
MM MM O O D D U U L E F
M M M O O D D U U L EEEE FFFF
M M O O D D U U L E F
M M OOO DDDD UUU LLLLL EEEEE F VERSION 92
DATE : 19/02/93
AUTEUR : pate
NOM DE LA S.D.E MAIL
t4mail1
++ OPEN(10,FILE='t4mail1',SPEC='OLD,UNFORMATTED',RECL=0)
NOM DE LA S.D.E COOR
t4coor1
++ OPEN(11,FILE='t4coor1',SPEC='OLD,UNFORMATTED',RECL=0)
NOM DE LA S.D.S BDCL
t4bdcl1
++ OPEN(12,FILE='t4bdcl1',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COBDC1 :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COTYNO :
FIN DU MODULE COTYNO
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CALMAI :
FIN DU MODULE CALMAI
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE COBDC1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
IMPRESSION DE LA S.D. BDCL DE NIVEAU 1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TITRE :
DATE ET NOM UTILISATEUR : 19/02/93 pate
TYPE DE LA STRUCTURE DE DONNEES : BDCL
NIVEAU ET NUMERO D'ETAT : 1 0
NOMBRE DE TABLEAUX ASSOCIES : 0
TABLEAU B D C 2
----------------
TYPE DES VALEURS DE BLOCAGE (NTYB) : 2
NOMBRE DE CARTES DECRIVANT LES BLOCAGES (NCART) : 81
NOMBRE DE RELATIONS LINEAIRES DE BLOCAGE (NCLRL) : 0
NUMERO D'OPTION DE STOCKAGE (NOPTFI) : 0
NOMBRE DE MOTS DU TABLEAU BDC3 (NMMAT3) : 243
NOMBRE DE MOTS DU TABLEAU BDC4 (NMMAT4) : 81
NOMBRE DE MOTS DU TABLEAU BDC5 (NMMAT5) : 0
NOMBRE DE MOTS DU TABLEAU BDC6 (NMMAT6) : 0
TABLEAUX B D C 3 B D C 4
-----------------------------
BLOCAGE TYPE : 1 : NOEUD : 1 , D.L. : 1
A LA VALEUR : 0.2000000E+01
BLOCAGE TYPE : 1 : NOEUD : 1 , D.L. : 2
A LA VALEUR : -0.2000000E+01
BLOCAGE TYPE : 1 : NOEUD : 1 , D.L. : 3
A LA VALEUR : -0.2000000E+01
BLOCAGE TYPE : 1 : NOEUD : 2 , D.L. : 1
A LA VALEUR : 0.1000000E+01
BLOCAGE TYPE : 1 : NOEUD : 2 , D.L. : 2
A LA VALEUR : -0.2000000E+01
BLOCAGE TYPE : 1 : NOEUD : 2 , D.L. : 3
A LA VALEUR : 0.0000000E+00
BLOCAGE TYPE : 1 : NOEUD : 3 , D.L. : 1
A LA VALEUR : 0.1765625E+01
BLOCAGE TYPE : 1 : NOEUD : 3 , D.L. : 2
A LA VALEUR : -0.1750000E+01
BLOCAGE TYPE : 1 : NOEUD : 3 , D.L. : 3
A LA VALEUR : -0.2000000E+01
BLOCAGE TYPE : 1 : NOEUD : 5 , D.L. : 1
A LA VALEUR : 0.1765625E+01
}
Notre exemple est un problème de thermique bidimensionnel, le domaine d'étude est représenté figure 4.1.
Le problème est posé de la façon suivante :
Trouvez u(x) (la température) telle que,
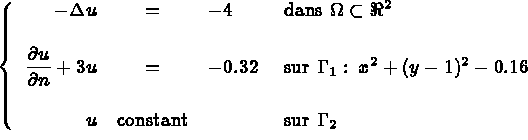
Nous choisissons une formulation variationnelle en température, les conditions aux limites forcées sont de type conditions aux limites en relation linéaire, elles peuvent encore s'écrire :
Pour résoudre ce problème, on choisit une interpolation de type P2 Lagrange droit et
isoparamétrique, les éléments finis correspondants sont TRIA 2P2D et TRIA 2P2C, l'inconnue variationnelle est u
la température. Il y a un seul degré de liberté de mnémonique VN
et les points et les noeuds ne coïncident pas partout (cf
éléments TRIA 2P2D -TRIA 2P2C).
La S.D. NOPO est pratiquement identique à celle du test 4 décrit
[4] dans [Guide Modulef - 1], il suffit d'ajouter des noeuds au
au milieu de chacune des arêtes des triangles.
La construction des S.D. MAIL et COOR est donnée en annexe D.
Le programme appelant le module COBDC1 est défini comme suit : {
1 PROGRAM T2BDCL
2 C +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
3 C BUT : BLOCAGE DES CONDITIONS AUX LIMITES EN RELATIONS LINEAIRES
4 C ...................................................................
5 C ELEMENT 2P2D ET 2P2C
6 C
7 C S.D.E. : MAIL COOR DE NOM RESPECTIF T4MAIL ET T4COOR
8 C
9 C S.D.S. : BDCL
10 C +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
11 C
12 C PROGRAMMEUR P. PATE INRIA - SIMULOG JUIN 92
13 C ...................................................................
14 C
15 PARAMETER ( LM = 45000 )
16 COMMON M(LM)
17 DOUBLE PRECISION DM
18 EQUIVALENCE (M(1),DM)
19 C
20 INTEGER NNN, IMPRE
21 CHARACTER*80 NOMFIC
22 DIMENSION NOFR(1,1),VAL(1)
23 REAL VAL, VALCLR
24 DOUBLE PRECISION VALCLD
25 EXTERNAL VALCLR, VALCLD
26 C
27 100 FORMAT('NOM DE LA S.D.E MAIL') #F
28 110 FORMAT('NOM DE LA S.D.E COOR') #F
29 120 FORMAT('NOM DE LA S.D.S BDCL') #F
30 C 100 FORMAT('NAME OF THE INPUT D.S. MAIL') #GB
31 C 110 FORMAT('NAME OF THE INPUT D.S. COOR') #GB
32 C 120 FORMAT('NAME OF THE OUTPUT D.S. BDCL') #GB
33 C
34 C INITIALISATION
35 C --------------
36 NNN = 0
37 IMPRE = 5
38 CALL INITIS(M,LM,IMPRE,NNN)
39 IMPRIM = IINFO('I')
40 C
41 C OUVERTURE DES FICHIERS CONTENANT LES S.D. D'ENTREE MAIL ET COOR
42 C ----------------------------------------------------------------
43 WRITE(IMPRIM,100)
44 CALL LIBCAR(NOMFIC)
45 CALL TRUNIT(NFMAIL)
46 CALL OUVRIS(NFMAIL,NOMFIC,'OLD,UNFORMATTED',0)
47 NIMAIL = 1
48 C
49 WRITE(IMPRIM,110)
50 CALL LIBCAR(NOMFIC)
51 CALL TRUNIT(NFCOOR)
52 CALL OUVRIS(NFCOOR,NOMFIC,'OLD,UNFORMATTED',0)
53 NICOOR = 1
54 C
55 C OUVERTURE DU FICHIER CONTENANT LA S.D. DE SORTIE BDCL
56 C ------------------------------------------------------
57 WRITE(IMPRIM,120)
58 CALL LIBCAR(NOMFIC)
59 CALL TRUNIT(NFBDCL)
60 CALL OUVRIS(NFBDCL,NOMFIC,'UNFORMATTED',0)
61 NIBDCL = 1
62 NTBDCL = 0
63 C
64 C S.D. NDL1
65 C ---------
66 C IL EST INUTILE DE CREER LA S.D. NDL1 CAR LE NOMBRE DE DEGRE
67 C DE LIBERTE PAR NOEUD EST CONSTANT (1)
68 C
69 NFNDL1 = 0
70 NINDL1 = 0
71 C
72 C APPEL DU MODULE CORNOE => CREATION DE LA S.D. COOR CONTENANT
73 C ---------------------- LES COORDONNEES DES NOEUDS
74 C
75 NFCOOS = 0
76 NICOOS = 2
77 NTCOOS = 0
78 CALL CORNOE(M,NFMAIL,NIMAIL,NFCOOR,NICOOR,NFCOOS,NICOOS,
79 + NTCOOS)
80 C
81 C INITIALISATION DES PARAMETRES DU MODULE COBDC1
82 C ----------------------------------------------
83 C
84 C LES INCONNUES BLOQUEES NE SONT PAS DECRITES SOUS FORME DE TRIPLET
85 NBFR = 0
86 C ON TRAVAILLE EN SIMPLE PRECISION
87 NTY = 2
88 C ON INDIQUE SI LES S.D. MAIL TYNO MPLR EXISTE OU NON
89 IEMAIL = 1
90 IETYNO = 0
91 NFTYNO = 0
92 NITYNO = 1
93 IEMPLR = 0
94 NFMPLR = 0
95 NIMPLR = 1
96 NOPFI = 0
97 C
98 C
99 ICONST = 0
100 C
101 C LES CONDITIONS AUX LIMITES EN RELATIONS LINEAIRES SONT
102 C FOURNIES A L'AIDE DU SOUS-PROGRAMME SPCLRL
103 NCLRL = -1
104 NMTRL = 0
105 ITA5 = 1
106 ITA6 = 1
107 FONINT = .FALSE.
108 C
109 C APPEL DE COBDC1
110 C ---------------
111 CALL COBDC1(M,ICONST,NBFR,NOFR,NTY,VAL,NCLRL,NMTRL,ITA5,ITA6,
112 + IEMAIL,NFMAIL,NIMAIL,IETYNO,NFTYNO,NITYNO,IEMPLR,NFMPLR,
113 + NIMPLR,NFNDL1,NINDL1,NFCOOS,NICOOS,NFBDCL,NIBDCL,NTBDCL,
114 + NOPFI,FONINT,VALCLR,VALCLD)
115 C
116 C IMPRESSION DE LA S.D. BDCL
117 C --------------------------
118 CALL IMBDCL(M,NFBDCL,NIBDCL,IMPRE)
119 C
120 C FERMETURE DE FICHIERS
121 C ---------------------
122 CLOSE(NFMAIL)
123 CLOSE(NFCOOR)
124 CLOSE(NFBDCL)
125 END
126 C
}
Remarques 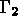 . Il y a donc n-1 relations linéaires à
deux termes qui lient ces noeuds :
. Il y a donc n-1 relations linéaires à
deux termes qui lient ces noeuds :
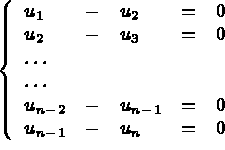
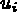 ne sera pivot de plusieurs relations
linéaires.
ne sera pivot de plusieurs relations
linéaires.{
1 SUBROUTINE SPCLRL(M,NOEFF,NOFR,NNR,NBNOE,NUNOE,COO4,NDIM,NCLRL,
2 + NMTRL,BDC5,LB5,BDC6,LB6,EPS)
3 C +++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++++
4 C BUT : ECRIRE LES CONDITIONS AUX LIMITES EN RELATION LINEAIRE
5 C --
6 C LA TEMPERATURE EST CONSTANTE SUR LA REFERENCE 2
7 C ....................................................................
8 C
9 C PARAMETRES D'ENTREE :
10 C
11 C M : SUPER TABLEAU M
12 C NOEFF : NOMBRE DE NOEUDS REFERENCES
13 C NOFR(NNR) : LISTE DE TOUS LES NUMEROS DE REFERENCE ( NOFR(I) = I )
14 C NBNOE(NNR) : NBNOE(I) = NOMBRE DE NOEUDS SUR LA REFERENCE I
15 C NUNOE(NOEFF): LISTE DES NOEUDS POUR CHAQUE REFERENCE
16 C COO4 : TABLEAU DES COORDONNEES
17 C NDIM : DIMENSION DE L'ESPACE
18 C
19 C PARAMETRES DE SORTIE :
20 C
21 C 1-ERE PASSAGE : NCLRL = -1
22 C NCLRL : NOMBRE DE CONDITIONS AUX LIMITES EN RELATIONS LINEAIRES
23 C NMTRL : NOMBRE MAXIMUM DE TERME EN RELATION LINEAIRE
24 C EPS : EPSILON POUR TRIER LES NOEUDS (EPS < 0. => PAS DE TRIE)
25 C 2-EME PASSAGE
26 C ON REMPLIT LE TABLEAU BDC5 ET BDC6 DE LA S.D.S. BDCL
27 C LB5 = 0
28 C LB6 = 0
29 C BOUCLE I SUR NCLRL
30 C LB5 = LB5 + 1
31 C BDC5(LB5) = NOMBRE DE TERME DE LA I-EME RELATION LINEAIRE
32 C LB6 = LB6 + 1
33 C BDC6(LB6) = VALEUR FINALE DE LA I-EME RELATION LINEAIRE
34 C BOUCLE J SUR LE NOMBRE DE TERME DE LA I-EME RELATION LINEAIRE
35 C LB5 = LB5 + 1
36 C BDC5(LB5) = NUMERO DU NOEUD
37 C LB5 = LB5 + 1
38 C BDC5(LB5) = DEGRE DE LIBERTE ASSOCIE
39 C LB6 = LB6 + 1
40 C BDC6(LB6) = VALEUR DU COEFFICIENT ASSOCIE AU J-EME TERME
41 C FIN BOUCLE SUR J
42 C FIN BOUCLE SUR I
43 C LB6 = LB6 * NBREMO
44 C ....................................................................
45 INTEGER M(*), NOEFF, NOFR(NNR), NNR, NBNOE(NNR), NUNOE(*), NDIM,
46 + NCLRL, NMTRL, BDC5(*), LB5, LB6
47 INTEGER NUMREF, IA, I
48 REAL COO4(NDIM,*), EPS, BDC6(*)
49 C
50 NUMREF = 2
51 IF(NCLRL .EQ. -1) THEN
52 C -- ON CALCULE LE NCLRL
53 NMTRL = 2
54 NCLRL = NBNOE(NUMREF) - 1
55 C ON NE FAIT PAS DE TRI SUR LES NOEUDS REFERENCES
56 EPS = - 0.001
57 C
58 ELSEIF(NCLRL .GT. 0) THEN
59 C --- ON REMPLIT LES TABLEAUX BDC5 CONTENANT :
60 LB5 = 0
61 LB6 = 0
62 C
63 C ON RECHERCHE A L'AIDE DU TABLEAU NBNOE LE DEBUT DE LA LISTE
64 C DES NOEUDS DE REFERENCE NUMREF DANS LE TABLEAU NUNOE
65 C
66 IA = 1
67 DO 2 I = 1 , NUMREF -1
68 IA = IA + NBNOE(I)
69 2 CONTINUE
70 C
71 C ON REMPLIT LES TABLEAUX BDC5 ET BDC6
72 C
73 DO 3 I = 1 , NCLRL
74 BDC5(LB5+1) = 2
75 BDC6(LB6+1) = 0.
76 C
77 C -- NOEUD1 , DL1 , APHA1
78 BDC5(LB5+2) = NUNOE(IA)
79 BDC5(LB5+3) = 1
80 BDC6(LB6+2) = 1.
81 C
82 C -- NOEUD2 , DL2 , APHA2
83 BDC5(LB5+4) = NUNOE(IA+1)
84 BDC5(LB5+5) = 1
85 BDC6(LB6+3) = -1.
86 C
87 C -- REMISE A JOUR DES COMPTEURS
88 LB5 = LB5 + 5
89 LB6 = LB6 + 3
90 IA = IA +1
91 3 CONTINUE
92 END IF
93 END
}
Nous faisons maintenant quelques remarques sur ce sous-programme :
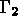 - 1,
- 1,
M M OOO DDDD U U L EEEEE FFFFF
MM MM O O D D U U L E F
M M M O O D D U U L EEEE FFFF
M M O O D D U U L E F
M M OOO DDDD UUU LLLLL EEEEE F VERSION 92
DATE : 19/02/93
AUTEUR : pate
NOM DE LA S.D.E MAIL
t4mail
++ OPEN(10,FILE='t4mail',SPEC='OLD,UNFORMATTED',RECL=0)
NOM DE LA S.D.E COOR
t4coor
++ OPEN(11,FILE='t4coor',SPEC='OLD,UNFORMATTED',RECL=0)
NOM DE LA S.D.S BDCL
t4bdcl
++ OPEN(12,FILE='t4bdcl',SPEC='UNFORMATTED',RECL=0)
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CORNOE :
FIN DU MODULE CORNOE
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE COBDC1 :
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
MODULE CALMAI :
FIN DU MODULE CALMAI
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
FIN DU MODULE COBDC1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
IMPRESSION DE LA S.D. BDCL DE NIVEAU 1
&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&
TITRE :
DATE ET NOM UTILISATEUR : 19/02/93 pate
TYPE DE LA STRUCTURE DE DONNEES : BDCL
NIVEAU ET NUMERO D'ETAT : 1 0
NOMBRE DE TABLEAUX ASSOCIES : 0
TABLEAU B D C 2
----------------
TYPE DES VALEURS DE BLOCAGE (NTYB) : 2
NOMBRE DE CARTES DECRIVANT LES BLOCAGES (NCART) : 0
NOMBRE DE RELATIONS LINEAIRES DE BLOCAGE (NCLRL) : 52
NUMERO D'OPTION DE STOCKAGE (NOPTFI) : 0
NOMBRE DE MOTS DU TABLEAU BDC3 (NMMAT3) : 0
NOMBRE DE MOTS DU TABLEAU BDC4 (NMMAT4) : 0
NOMBRE DE MOTS DU TABLEAU BDC5 (NMMAT5) : 260
NOMBRE DE MOTS DU TABLEAU BDC6 (NMMAT6) : 156
TABLEAUX B D C 5 B D C 6
-----------------------------
NOMBRE DE TERMES : 2
TERME 1 NOEUD 2 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 3 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 3 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 4 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 4 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 5 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 5 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 7 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 7 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 8 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 8 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 9 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 9 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 10 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 10 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 11 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 11 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 16 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
NOMBRE DE TERMES : 2
TERME 1 NOEUD 16 D.L. 1 COEFFICIENT 0.1000000E+01
TERME 2 NOEUD 17 D.L. 1 COEFFICIENT -0.1000000E+01
SECOND MEMBRE DE LA COMBINAISON : 0.0000000E+00
}