Suiv.: Les éléments finis élastiques Sup.: 1 Introduction Préc.: Modélisation mathématique d'un problème Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: Les éléments finis élastiques
Sup.: 1 Introduction
Préc.: Modélisation mathématique d'un problème
Index
Table des matières
La méthode des éléments finis consiste à chercher une solution approchée du problème 1.2 en se
plaçant dans un espace 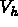 de dimension finie. La résolution se déroule en plusieurs étapes :
de dimension finie. La résolution se déroule en plusieurs étapes :
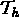 ) du domaine
à considérer ;
) du domaine
à considérer ;
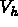 ;
;
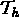 , i.e. à la
(aux) matrice(s), au second membre du système et aux contraintes ;
, i.e. à la
(aux) matrice(s), au second membre du système et aux contraintes ;
Quelques détails sur ces différentes étapes :
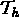 consiste à recouvrir le domaine à l'aide d'éléments
géométriques de manière aussi fidèle que possible
(h fait référence à la taille des éléments) ;
consiste à recouvrir le domaine à l'aide d'éléments
géométriques de manière aussi fidèle que possible
(h fait référence à la taille des éléments) ;
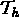 le couple (
le couple (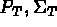 ) avec :
) avec :
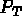 un espace, généralement polynômial, de dimension finie
un espace, généralement polynômial, de dimension finie 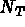 ,
,
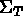 un ensemble de
un ensemble de 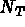 degrés de liberté
degrés de liberté
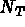 formes linéaires
formes linéaires 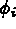 1
1 i
i 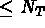 définies sur l'espace
définies sur l'espace 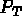 . Le triplet (
. Le triplet (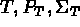 ) est un élément fini si l'ensemble
) est un élément fini si l'ensemble
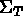 est
est 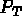 unisolvant c'est à dire s'il existe
unisolvant c'est à dire s'il existe 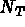 fonctions
fonctions
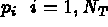 de l'espace
de l'espace 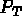 linéairement indépendantes, telles que :
linéairement indépendantes, telles que :
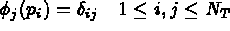
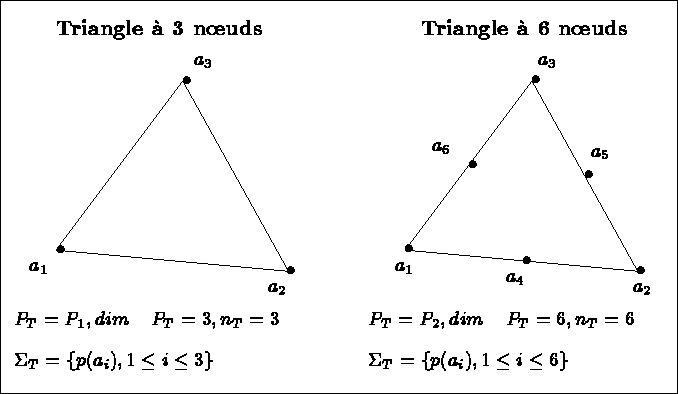
Figure: Deux exemples d'élément fini
Prenant l'exemple du triangle à 3 noeuds correspondant à l'interpolation de Lagrange de degré 1 (cf figure 1.1) on a :
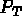 =
=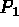 : les polynômes de degré inférieur ou égal à 1
en x et y,
: les polynômes de degré inférieur ou égal à 1
en x et y, 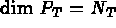 =3
=3
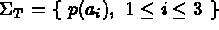 et,
et, 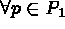 ,
, 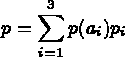 avec
avec 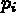 =
=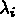 (coordonnées barycentriques).
(coordonnées barycentriques).
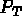 =
= 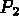 les polynômes de degré inférieur ou égal
à 2 en x et y,
les polynômes de degré inférieur ou égal
à 2 en x et y, 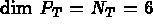
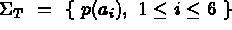 et,
et, 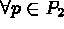 ,
, 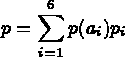
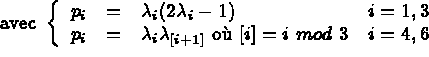
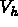 , espace des fonctions
, espace des fonctions 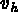 ayant
une certaine régularité, dont
la restriction à T est un élément de
ayant
une certaine régularité, dont
la restriction à T est un élément de 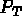 . Si on considère des éléments finis de Lagrange conformes
(comme ceux de l'exemple ci-dessus),
la condition aux limites étant u=
. Si on considère des éléments finis de Lagrange conformes
(comme ceux de l'exemple ci-dessus),
la condition aux limites étant u=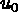 sur
sur 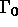 (une partie de la frontière
(une partie de la frontière
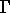 ),
le problème 1.2 s'écrit :
),
le problème 1.2 s'écrit :
avec 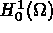 l'espace de solution classique et
l'espace de solution classique et
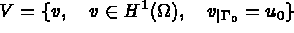
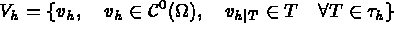
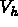 étant fait, le problème s'écrit maintenant :
étant fait, le problème s'écrit maintenant :
En pratique ce problème (1.4) conduit à des calculs d'intégrales qui s'avèrent, sauf cas d'espèce, impossibles. On est donc amené à utiliser des schémas d'intégration numérique et par suite à résoudre, le problème 1.5, un problème approché du précédent.
où 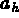 (.,.) est une approximation de la forme bilinéaire a et
(.,.) est une approximation de la forme bilinéaire a et
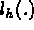 une approximation de la forme linéaire l obtenues par utilisation de
l'intégration numérique.
une approximation de la forme linéaire l obtenues par utilisation de
l'intégration numérique.