Suiv.: 5 Cas des coques Sup.: 4 Cas des plaques Préc.: Modélisation sous forme d'équations aux Index Table des matières

4.2 Formulations variationnelles

Formulation en déplacement

Dans le cas d'une plaque encastrée (cas ci-dessus), une formulation possible est la suivante:

Trouver, à chaque instant t, la flèche w dans l'espace

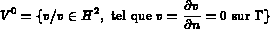
solution de :

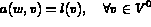
ou après discrétisation trouver, à chaque instant t, la flèche 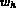dans l'espace

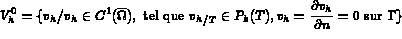
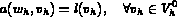
avec :

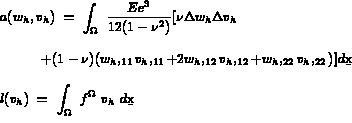
Autres formulations

L'idée est d'introduire une deuxième inconnue u liée à w par des relations différentes (ce qui donne différentes méthodes) et à découper le problème sous la forme :

Trouver, à chaque instant t, le couple (u,w) dans l'espace 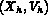solution de

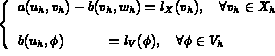
avec des choix différents pour les espaces 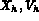et les opérateurs .

La formulation mixte de type Hellan-Hermann-Johnson

correspond aux choix suivants :

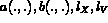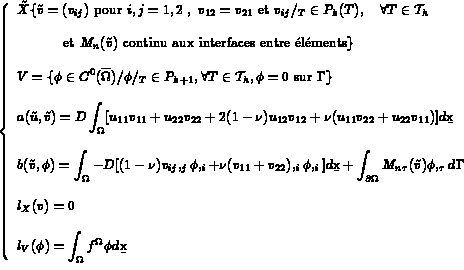
Par cette méthode on obtient une solution 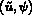telle que 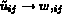et .

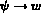Pour la valeur k=0 , l'expression b(.,.) se simplifie en

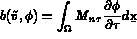
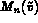et par introduction de multiplicateurs de Lagrange, il n'est pas nécessaire d'imposer la continuité des moments aux interfaces.

On introduit l'espace:

et la forme bilinéaire c(.,.) définie par:

où

le problème se réécrit sous la forme:

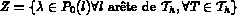
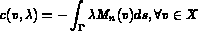
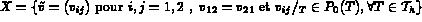
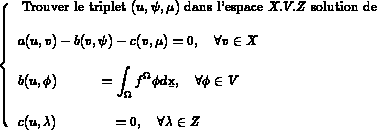
On résout ce système (c'est l'exemple de l'élément TRIA HHJ1).

Une formulation hybride duale

correspond aux choix suivants :

Pour chaque entier m>0,r>2,s>0 on définit:

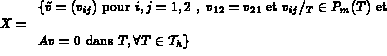
avec

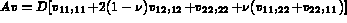
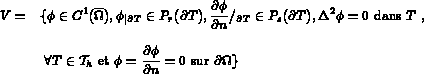
et le choix

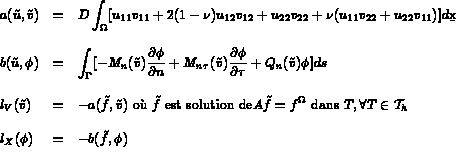
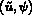permet d'obtenir une solution qui pour le choix r=3,s=m=1, c'est-à-dire l'élément TRIA H31D, est telle que 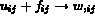dans T et 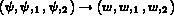aux interfaces entre éléments.