




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 1.5.9 Index
Up: The EMC˛
preprocessor
Prev: 1.5.7 Limitations and bugs
Index
Contents
We use a system of lists with two elements, which we call CAR and CDR.
The empty address is NIL=0 (parameter).
In the following pictures, CAR will always be on the left and CDR on the
right.
The free atoms are in a list of free atoms. The beginning of this list is FREE.
Free atoms are linked through their CDR.
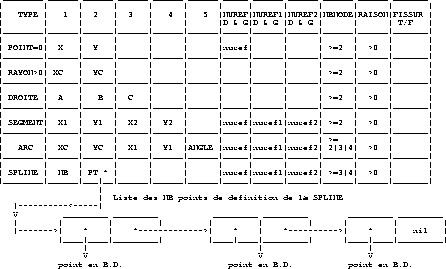
Figure 1.44: Description of the DB for the CONSTRUCTION application
Figure 1.44 describes the DB for the CONSTRUCTION
application with,
- TYPE
- the type of DB element
- POINT = 0. X,Y POINT.
- RADIUS > 0. CIRCLE of center XC,YC and radius RADIUS.
- LINE = -1. STRAIGHT LINE of equation A*x + B*y + C =0
with A*A + B*B = 1
- SEGMENT = -3. SEGMENT going from point X1,Y1 to point
X2,Y2.
- ARC = -2. ARC of center XC,YC passing through
point X1,Y1
and with an angle ANGLE from this point.
- SPLINE = -4. SPLINE.
- EMPTY = -1000. empty element.
for SPLINE,
- NB is the number of definition points.
- PT is the pointer on the list of definition POINTS of the SPLINE.
- NUREF is the reference number of the element
(ARC or SEGMENT). Default: NUREF=0.
- NUREF1 is the reference number of extremity 1 of the element (ARC
or SEGMENT). Default: NUREF1=0.
- NUREF2 is the reference number of extremity 2 of the element (ARC
or SEGMENT). Default: NUREF2=0.
- NBNODE is the number of intermediate points in the element
(extremities are included). Default: NBNODE=2.
- RATIO is the ratio of the geometric progression used to distribute the
NBNODE-2 points from extremity 1 to extremity 2. Default: RATIO=1.
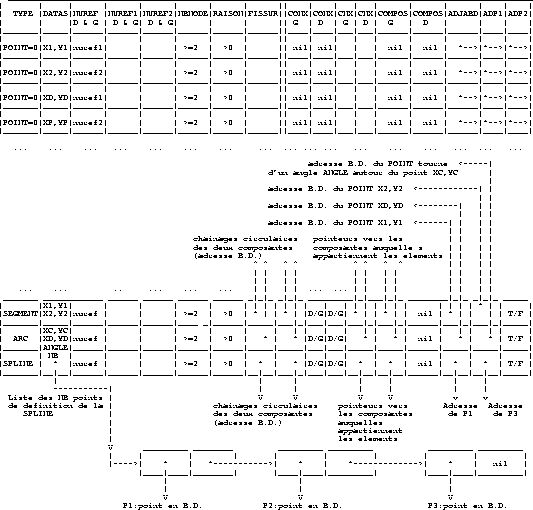
Figure 1.45: Description of the DB for the PREP MESH application
Figure 1.45 describes the DB for the PREP MESH
application, where
- TYPE
- is the type of DB element
- POINT = 0. X,Y POINT.
- SEGMENT = -3. SEGMENT going from point X1,Y1 to point
X2,Y2.
- ARC = -2. ARC of center XC,YC passing through
point X1,Y1 and with an angle ANGLE from this point.
- SPLINE = -4. SPLINE.
- EMPTY = -1000. empty element.
- NUREF
- is the reference number of the element
(ARC or SEGMENT).
- ADP1
- DB pointer on the POINT extremity 1 of the
element
(If the element is not cracked, NUREF of this POINT contains the
reference number of extremity 1 of the element).
- ADP2
- DB pointer on the POINT extremity 2 of the
element or on the last POINT of the SPLINE.
(If the element is not cracked, NUREF of this POINT contains the
reference number of extremity 2 of the element).
- NBNODE
- is the number of intermediate points in the element
(extremities are included).
- RATIO
- is the ratio of the geometric progression used to distribute the
NBNODE-2 points from extremity 1 to extremity 2.
- CONX(2)
- DB pointers, used for the circular chaining of the
elements of a connex component. Given one element, there are two and only
two connex component that contain this element: the left component and the
right component (left and right are relative to the orientation of the
element). There are thus two chainings denoted by CONXG and CONXD.
- CNX(2)
- indicates which CONX is to be used for the next element
(CONXG or CONXD) depending on whether CNX equals LEFT or RIGHT
(LEFT=1, RIGHT=2)(parameter).
- COMPOS(2)
- inverse pointers to the two components to which
the element belongs.
CNXG is associated with CONXG and COMPOSG (exist only for ARCS and
SEGMENTS).
CNXD is associated with CONXD and COMPOSD (exist only for ARCS and
SEGMENTS).
- ADJABD
- Beginning of the list of elements passing through the
point (exists only for
POINTS). (See the description of this list below).
The beginning of the list of elements passing through a point is
ADJABD.
Figure 1.46 describes the list of elements passing through
point i.
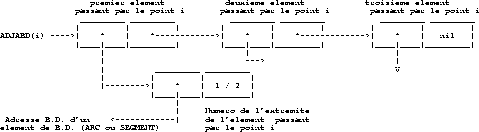
Figure 1.46: Description of the list of elements passing through point i
The beginning of the list of components is COMP.
Figure 1.47 describes the list of components.
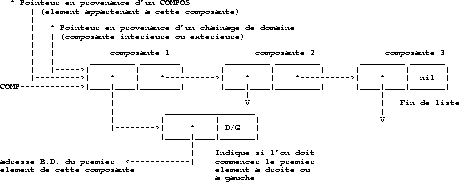
Figure 1.47: Description of the list of components
The beginning of the list of domains is SDOMN.
Figure 1.48 describes the list of domains.
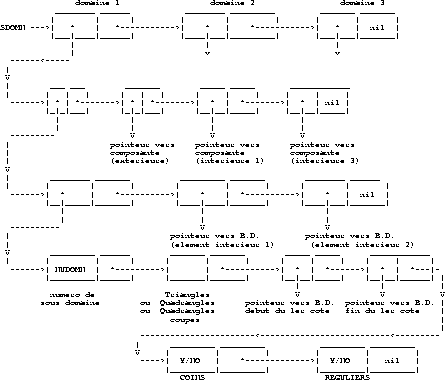
Figure 1.48: Description of the list of domains
The DB is the same as in the PREP_MESH application and the data
structure DS_MESH is as follows:
- nbs
- is the number of the last vertex
- nbt
- is the number of the last triangle
- nba
- is the number of edges that lie on curves (segment, arc, spline)
that we will call boundary edges
- nbsd
- is the number of subdomains
- nbsrft
- is the number of vertices that are referenced by the
elements
- nbtria
- is the number of triangles
- nbquad
- is the number of quadrangles
- nbtrou
- is the number of holes in the mesh
- freetr
- is the beginning of the list of detroyed triangles
- finbd3
- is the number of the last DB element of PREP_MESH
- The vertices
- are defined in the following four parallel arrays:
- cr(1:2,nbs)
- is the array of vertex coordinates.
- nsorig(1:nbs)
- is the array giving the original vertex number of
vertices that lie on a crack. The actual coordinates of vertex i are
cr(1:2,nsorig(i)), while coordinates cr(1:2,i) are only used to visualize
the crack.
Note: if vertex i is not on a crack, then nsorig(i) =
i.
- abcurv(1:nbs)
- is:
- 0 if the vertex is not on a curve (segment, arc, spline),
i.e. is an internal vertex of a subdomain,
- the abscissa of the point on a curve if this vertex is not an
extremity of the curve,
0 if this vertex is the extremity of a curve. Note: curves are
always parametrized between 0 and 1.
- refs(1:nbs)
- is the array giving the DB number of the element
(point, segment, arc, spline) that supports the vertex, if it exists, or 0
otherwise.
Note: if the vertex is the extremity of a curve then the element in
question will be the point extremity of the curve (cf. ADP1 and ADP2
(Appendix 1.5.8))
- The finite elements
- are triangles or quadrangles, which are
internally represented with triangles whose edges are visible or not. This is
used to draw the quadrangles.
The arrays that define the triangles are:
- nsea(1:6,nbt)
- gives for each triangle the vertices and
the adjacent triangles or boundaries edges. If nsea(1,ie)< 1 then triangle ie does not exist
and reft(ie) gives the next destroyed triangle. Otherwise, triangle ie
exists and
- nsea(1:3,ie) gives for each triangle the vertex numbers
counterclocwise.
-
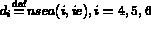 , the
3 edges
, the
3 edges 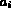 of the triangle numbered from 4 to 6 have as vertices
nsorig(nsea(i-3,ie)) and (nsorig(nsea(mod(i,3)+1,ie)).
of the triangle numbered from 4 to 6 have as vertices
nsorig(nsea(i-3,ie)) and (nsorig(nsea(mod(i,3)+1,ie)).
- if
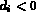 the edge is a boundary edge. It is defined in
aretdb with number
the edge is a boundary edge. It is defined in
aretdb with number 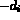 ,
,
- otherwise the edge is internal and
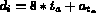 where
where 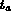 is the number of the triangle adjacent to the edge
and
is the number of the triangle adjacent to the edge
and 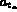 is the number of the edge in
is the number of the edge in 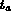 .
.
- anovue(1:nbt)
- gives the visibility of the 3 edges for each
triangle. If anovue(i) equals
- 0
- all the edges of triangle i are visible,
- 1
- only edge 4 of triangle i is not visible,
- 2
- only edge 5 of triangle i is not visible,
- 3
- only edge 6 of triangle i is not visible.
- reft(1:nbt)
- is:
- The boundary edges
- of the mesh are defined as follows:
- aretbd(1:2,nba)
- gives for each edge its two vertex numbers,
- areadj(gauche:droite,nba)
- :
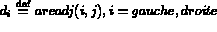 same definition as nsea,
same definition as nsea,
- refa(nba)
- gives the DB address of the support of the edge,
which always exists by definition.
- The subdomains
- are defined in the following arrays:
- refsd(nbsd)
- gives the reference numbers of subdomains, if
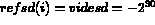 then the subdomain does not exist.
then the subdomain does not exist.
- trfsd(3,3,i)
- gives the transformation applied to subdomain
ptorsd(i) to obtain this subdomain
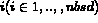 .
.
- strfsd(i)
- gives the sign of the transformation
(for example: -1 for a symmetry with respect to a straight line)
- ptorsd(i)
- gives the number of the original subdomain
(if ptorsd(i)=i then subdomain i is not transformed
(original subdomain))
- tetsd(nbsd)
- is an array that gives for each subdomain the first
triangle of the list of triangles of this subdomain (cf. reft)
The mesh is only composed of triangles and can be defined with the help of
the following two integers and four arrays:
- nbt
- is the number of triangles
- nbs
- is the number of vertices
- nu(1:3,1:nbt)
- is an integer array giving the three vertex numbers
counterclockwise for each triangle.
- c(1:2,nbs)
- is a real array giving the 2 coordinates of each vertex.
- refs(nbs)
- is an integer array giving the reference numbers of the
vertices.
- reft(nbs)
- is an integer array giving the reference numbers of the
triangles.
Note: the vertices that are not referenced by a triangle will be eliminated. In
this case the vertex numbering will be compressed accordingly.
xxx.am files are read as follows:
open(1,file='xxx.am',form='unformatted',status='old')
read (1) nbs,nbt
read (1)
+ ((nu(i,j),i=1,3),j=1,nbt)
+ ,((c(i,j),i=1,2),j=1,nbs)
+ ,( reft(i),i=1,nbt)
+ ,( refs(i),i=1,nbs)
close(1)
xxx.am_fmt files are read as follows:
open(1,file='xxx.am_fmt',form='formatted',status='old')
read (1,*) nbs,nbt
read (1,*) ((nu(i,j),i=1,3),j=1,nbt)
read (1,*) ((c(i,j),i=1,2),j=1,nbs)
read (1,*) ( reft(i),i=1,nbt)
read (1,*) ( refs(i),i=1,nbs)
close(1)
xxx.amdba files are read as follows:
open(1,file='xxx.am_fmt',form='formatted',status='old')
read (1,*) nbs,nbt
read (1,*) (k,(c(i,k),i=1,2),refs(k),j=1,nbs)
read (1,*) (k,(nu(i,k),i=1,3),reft(k),j=1,nbt)
close(1)






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 1.5.9 Index
Up: The EMC˛
preprocessor
Prev: 1.5.7 Limitations and bugs
Index
Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()





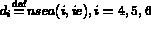 , the
3 edges
, the
3 edges 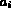 of the triangle numbered from 4 to 6 have as vertices
nsorig(nsea(i-3,ie)) and (nsorig(nsea(mod(i,3)+1,ie)).
of the triangle numbered from 4 to 6 have as vertices
nsorig(nsea(i-3,ie)) and (nsorig(nsea(mod(i,3)+1,ie)).
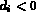 the edge is a boundary edge. It is defined in
aretdb with number
the edge is a boundary edge. It is defined in
aretdb with number 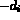 ,
,
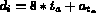 where
where 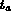 is the number of the triangle adjacent to the edge
and
is the number of the triangle adjacent to the edge
and 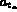 is the number of the edge in
is the number of the edge in 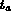 .
.
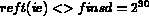 , see also the tetdt array
for the beginnings of lists of subdomains.
, see also the tetdt array
for the beginnings of lists of subdomains.
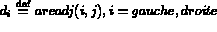 same definition as nsea,
same definition as nsea,
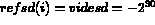 then the subdomain does not exist.
then the subdomain does not exist.
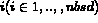 .
.