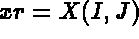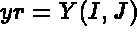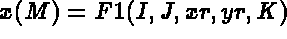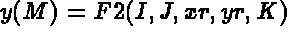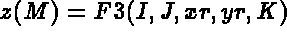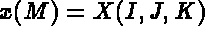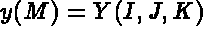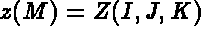




![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 3.4.4 Examples of use
Up: 3.4 Method for a hexahedral topology
Prev: 3.4.2 Description of the input data
Index
Contents
Different options are available to define the geometry, the splitting of the elements and the physical
attributes.
- The geometry: option IOPTM, arrays X,Y and H, functions F1, F2 and F3:
- IOPTM = 0: the mesh is of finite difference type with constant step in the 3 directions.
X, Y and H are three real values (declared as arrays) which represent the 3 spacing steps in the 3
directions. Every point, M, is referenced by its three indices I, J, and K and has coordinates:
- IOPTM = 1: the mesh is of finite difference type with variable step in the 2 first directions
and constant step in the third direction.
X an Y are two arrays of lengths N1 and N2, H is real (declared as an array); these values
enable us to find the coordinates of each point, M, with indices I, J and K, as follows:
- IOPTM = 2: the mesh is of finite difference type with variable step in the 3
directions. X, Y and H are three arrays of lengths N1, N2 and NB+1; these values
enables us to compute the coordinates of any point M, with indices I, J and K, as follows:
- IOPTM = 3: the mesh is of finite difference type with variable step in the 2 first directions
and a constant step in the third direction. X and Y are two arrays of length
N1
 N2 and H is real (declared as an array); these values are used to compute
the coordinates of any point M, with indices I, J and K, as follows:
N2 and H is real (declared as an array); these values are used to compute
the coordinates of any point M, with indices I, J and K, as follows:
- IOPTM = 4: the mesh is of finite difference type with variable step in the 2 first directions
and a variable step in the third direction. X and Y are two arrays of length
N1
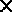 N2 and H is an array of length NB+1; these values are used to compute the coordinates of any
point M, with indices I, J and K, as follows:
N2 and H is an array of length NB+1; these values are used to compute the coordinates of any
point M, with indices I, J and K, as follows:
- IOPTM = 5: a mesh of finite difference type with constant step in the 2 first directions
used to construct the final mesh via the definition of points given by functions
F1, F2 and F3. X and Y are real (declared as arrays). we obtain the following construction:
and
- IOPTM = 6: a mesh of finite difference type with variable step in the 2 first directions
used to construct the final mesh via the definitions of the points given by functions
F1, F2 and F3. X and Y are two arrays of lengths N1 and N2. We obtain the following construction:
and
- IOPTM = 7: a mesh of finite difference type with variable step in the first 2 directions
used to construct the final mesh via the definitions of the points given by functions
F1, F2 and F3. X and Y are two arrays of lengths N1
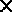 N2. We obtain the following construction:
and
N2. We obtain the following construction:
and
- IOPTM = < 0: a mesh of finite difference type with variable step in the 3 directions
used to construct the final mesh via the definitions of the points given by arrays
with indices X, Y and H (without verification).
- The splitting of elements: option NOPTDE:
- NOPTDE = 0: the result consists of hexahedra formed logically;
- NOPTDE = 1: each hexahedron is split into 2 pentahedra according to the direction
of the first bisector in the z=0 plane;
- NOPTDE = 2: each hexahedron is split into 2 pentahedra according to the direction
of the other diagonal;
- NOPTDE = 3: we first follow case NOPTDE = 1, then each pentahedron is split into 3 tetrahedra;
- NOPTDE = 4: the same with option NOPTDE = 2;
- NOPTDE = 5: each hexahedron is split into 5 tetrahedra.
- The physical attributes: sub-domain and reference numbers:
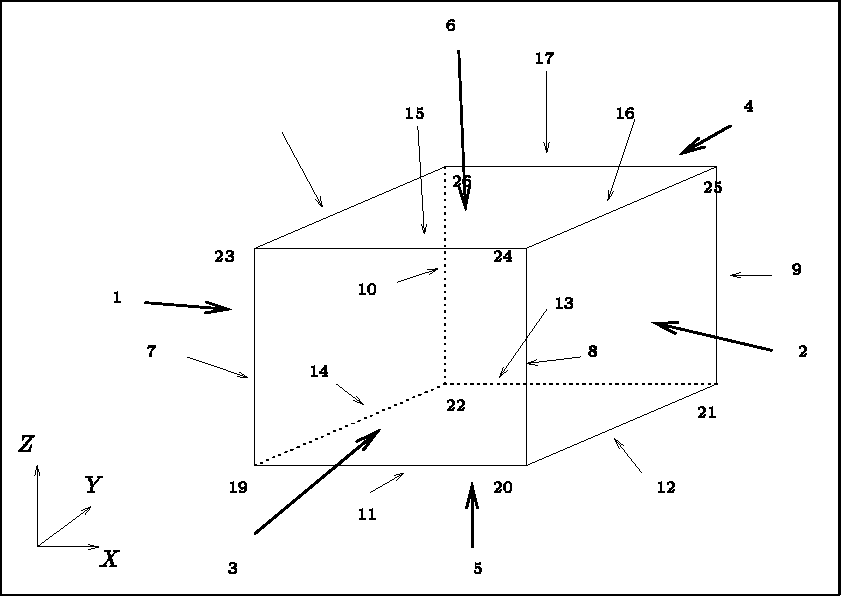
The point numbering is done according to the indications depicted in figure 3.30.
The element numbering is done analogously, layer by layer.
Figure 3.30: Point numbering by module GEL3D1
To call module GEL3D1 , it is necessary to write a main program as follows:
- dimension array M (in the blank common)
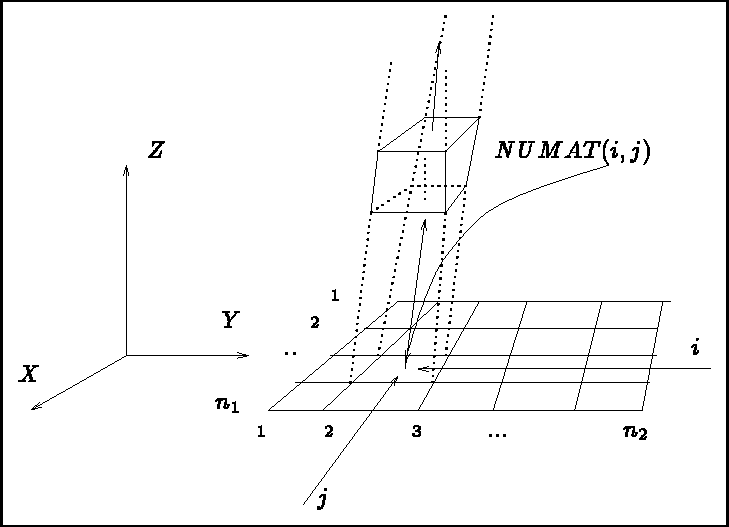
- declare the integer array NUMAT(.), array with 2 or 3 indices according to the case
- declare the integer array ITYP(NB) where NB is the number of layers
- declare the real array X(.), array with 1, 2 or 3 indices according to the case
- declare in the same way the real arrays Y(.) and H(.)
- declare the externals F1, F2 and F3 (according to the case)
- call INITI
- call the module
CALL GEL3D1 (M,IOPTM,JOPTSD,NOPTDE,N1,N2,NB,X,Y,H,
. F1,F2,F3,NUMAT,ITYP,NFNOPO,NINOPO,NFAUX)
where
- M is the super array
- IOPTM is the data description option
- JOPTSD is the sub-domain numbering option
- NOPTDE is the element splitting option
- N1 is the number of points in the x direction
- N2 is the number of points in the y direction
- NB is the number of layers (i.e. the number of points-1 in the z direction)
- X,Y and H are the arrays with 1, 2 or 3 indices to define the coordinates of the points
- F1, F2 and F3 are the names of the 3 external functions to supply (according to the value of IOPTM)
to define the point coordinates. These functions have the following form:
- F1(I,J,XR,YR,K) defines the abscissis of the points from I and J, the position of the point in the
plane of definition,
XR and YR, the coordinates of point with indices I and J, and K , the sectional index (i.e. K=1,NB+1)
- F2(I,J,XR,YR,K) has the same form and defines the ordinates of the points
- F3(I,J,XR,YR,K) has the same form and defines the sides of the points
- NUMAT is an array with 2 or 3 indices to assign the sub-domain numbers
- ITYP is the array determining the type of layers (array linked to NUMAT)
- NF(NI)NOPO is the support number of the O.D.S. NOPO and its level
- NFAUX has the value 0
Remark:
In order to change the references which are automatically assigned, either module MODNOP, or
preprocessor MODNXX, or the keyword NUME of APNOP3, can be used.






![[BIG]](../icons/zoom18.gif)
![[Normal]](../icons/zoom14.gif)
![[small]](../icons/zoom10.gif)
Next: 3.4.4 Examples of use
Up: 3.4 Method for a hexahedral topology
Prev: 3.4.2 Description of the input data
Index
Contents
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
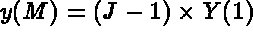
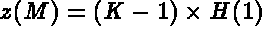
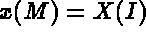
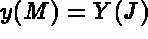
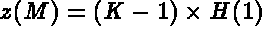
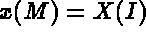
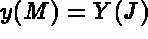
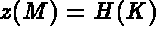
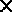 N2 and H is real (declared as an array); these values are used to compute
the coordinates of any point M, with indices I, J and K, as follows:
N2 and H is real (declared as an array); these values are used to compute
the coordinates of any point M, with indices I, J and K, as follows:
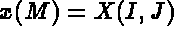
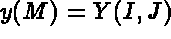
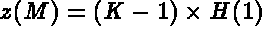
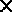 N2 and H is an array of length NB+1; these values are used to compute the coordinates of any
point M, with indices I, J and K, as follows:
N2 and H is an array of length NB+1; these values are used to compute the coordinates of any
point M, with indices I, J and K, as follows:
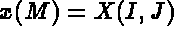
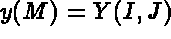
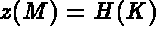
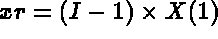
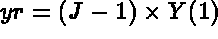
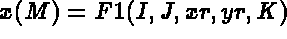
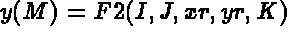
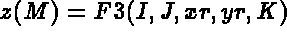
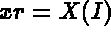
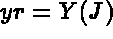
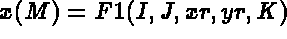
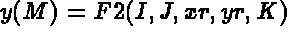
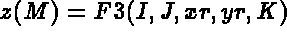
 N2. We obtain the following construction:
N2. We obtain the following construction: