Suiv.: 2.4 Cas des plaques Sup.: Les éléments finis élastiques Préc.: Elasticité bidimensionnelle Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 2.4 Cas des plaques
Sup.: Les éléments finis élastiques
Préc.: Elasticité bidimensionnelle
Index
Table des matières
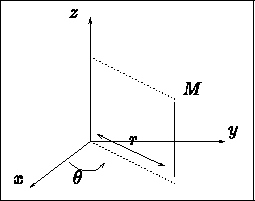
Figure: Coordonnées cylindriques
Par hypothèses sur la géométrie du domaine, tout point M(x,y,z) est complètement défini
par les variables 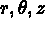 avec:
avec:

Le déplacement 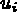 s'exprime avec ces variables comme:
s'exprime avec ces variables comme:

où 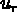 désigne le déplacement radial. Le déplacement est donc connu par
désigne le déplacement radial. Le déplacement est donc connu par 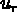 sa composante radiale et
sa composante radiale et 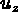 sa composante axiale qui sont les 2 inconnues cherchées.
sa composante axiale qui sont les 2 inconnues cherchées.
On suppose de plus que les données sont réparties de manière analogue, i.e. que
 s'exprime par
s'exprime par 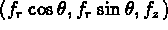 et que
et que 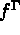 s'écrit sous
la même forme.
s'écrit sous
la même forme.
Comme on a :
le système général (i.e. le modèle 3D) s'écrit dans le cas isotrope :
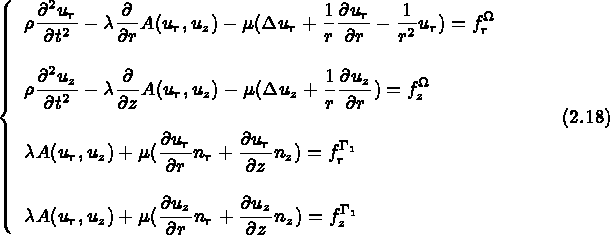
avec
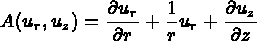
et où
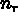 ,
, 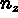 désignent les composantes de la normale à
désignent les composantes de la normale à 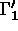 frontière déduite par
axisymétrie de
frontière déduite par
axisymétrie de 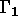 .
De plus, les conditions limites sont :
.
De plus, les conditions limites sont : 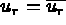 et
et 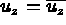 sur
sur 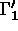 frontière déduite de
frontière déduite de 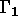 par axisymétrie.
par axisymétrie.
Plusieurs formulations variationnelles sont possibles, nous détaillons ici uniquement la formulation variationnelle en déplacement :
Trouver, dans l'espace 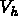 , à chaque instant t,
les déplacements
, à chaque instant t,
les déplacements 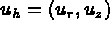 solution de :
solution de :
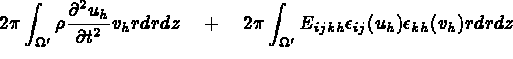
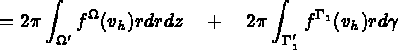
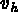 de
de 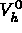 avec
avec
avec
avec
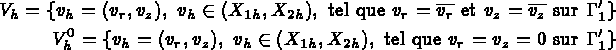
où les espaces  sont définis par :
sont définis par :
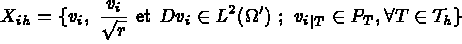
Le but de ce paragraphe est d'indiquer la démarche suivie lors de l'implémentation d'un élément fini pour calculer les quantités élémentaires.
Pour simplifier, on se place dans le cas stationnaire.
Le passage aux quantités élémentaires se fait de la même manière que dans le cas de la dimension 3 (cf paragraphe 2.1.3).
Soient 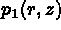 ,
, 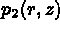 , ...,
, ..., 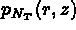 les
les 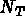 polynômes de base.
On note
polynômes de base.
On note
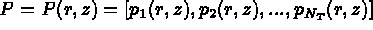
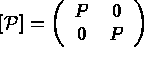
Alors,
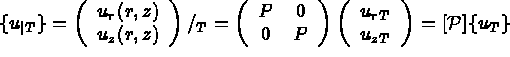
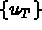 la restriction à T de { u } et
la restriction à T de { u } et 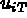 la composante i des valeurs
de la fonction u aux noeuds de l'élément T.
la composante i des valeurs
de la fonction u aux noeuds de l'élément T. Ensuite, on note
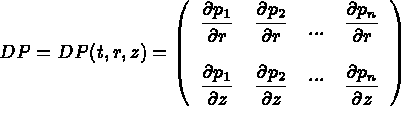
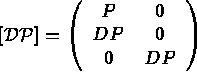
De même, on exprime 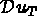 en fonction de
en fonction de 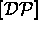 et de
et de 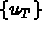 par
par
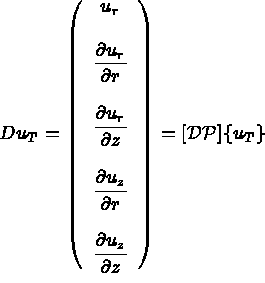
 et
et  s'écrivent :
s'écrivent :
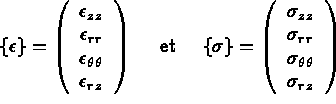
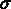 )
) 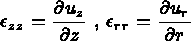
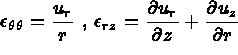
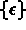 s'exprime en fonction de Du
s'écrit en fonction de
s'exprime en fonction de Du
s'écrit en fonction de 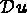 par
par 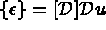 où
où 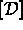 est la matrice des déformations i.e.
est la matrice des déformations i.e.
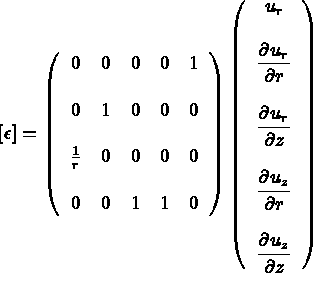
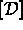 la matrice ci-dessus, ainsi
la matrice ci-dessus, ainsi
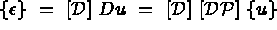
En utilisant la loi de comportement, on exprime { } en fonction de {
} en fonction de { } :
} :
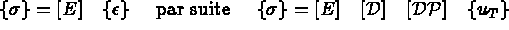
avec (sous sa forme générale):

On peut alors calculer sur chaque élément T :
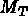 ] la matrice élémentaire de masse,
] la matrice élémentaire de masse,
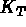 ] la matrice élémentaire de rigidité,
] la matrice élémentaire de rigidité,
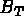 ] le second membre élémentaire et
] le second membre élémentaire et
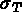 ] les contraintes élémentaires
] les contraintes élémentaires
Pour obtenir le système à résoudre, il suffit de construire les matrices et seconds membres globaux (voir également le cas de la dimension 3 paragraphe 2.1.4).