Suiv.: 3.2 Thermique bidimensionnelle Sup.: Les éléments finis thermiques Préc.: Les éléments finis thermiques Index Table des matières
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Suiv.: 3.2 Thermique bidimensionnelle
Sup.: Les éléments finis thermiques
Préc.: Les éléments finis thermiques
Index
Table des matières
Soit  la région de
la région de 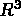 occupée par la structure dans son
état initial. On suppose que le milieu continu
occupée par la structure dans son
état initial. On suppose que le milieu continu  est soumis
à une distribution de puissance volumique de densité
est soumis
à une distribution de puissance volumique de densité 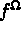 et à l'action
d'un flux de densité
et à l'action
d'un flux de densité 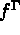 s'exerçant sur la partie
s'exerçant sur la partie 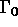 de la frontière
de la frontière 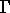 . On suppose de plus qu'une partie
. On suppose de plus qu'une partie 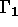 de
cette frontière est à une température imposée et que
de
cette frontière est à une température imposée et que 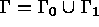 .
.
Le problème est de déterminer le champ des températures u
en tout point M de  ainsi que le champ des flux de température
ainsi que le champ des flux de température 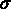 à tout instant t à partir de la configuration initiale donnée
à tout instant t à partir de la configuration initiale donnée 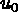 .
.
La formulation de ce problème en équations aux dérivées partielles (E.D.P.) est donnée ci-dessous :
avec
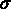 le flux de température
le flux de température
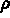 le produit de la masse thermique par la chaleur massique,
le produit de la masse thermique par la chaleur massique,
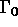 ,
,
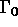 ,
,
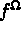 la puissance volumique appliquée à
la puissance volumique appliquée à

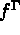 le flux appliqué sur
le flux appliqué sur 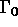 ,
,
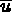 la température imposée sur
la température imposée sur 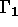 ,
,
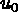 la température initiale (t=0),
la température initiale (t=0),
Plusieurs formulations variationnelles à un ou plusieurs champs sont possibles selon l'inconnue la plus importante à trouver : la température ou le flux.
Pour simplifier, seul le problème stationnaire est traité (le terme
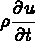 de 3.1 n'est pas considéré),
et la dépendance par rapport au temps t est volontairement négligée.
La variable d'espace (x,y,z) est désignée par
de 3.1 n'est pas considéré),
et la dépendance par rapport au temps t est volontairement négligée.
La variable d'espace (x,y,z) est désignée par  .
.
Le problème s'écrit comme suit :
Trouver, dans l'espace 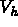 la température u solution de :
la température u solution de :

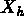 est défini par :
(
est défini par :
(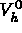 est l'espace
est l'espace 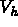 avec une condition aux limites homogène)
avec une condition aux limites homogène)
où l'espace 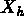 est défini par :
est défini par :
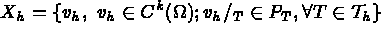
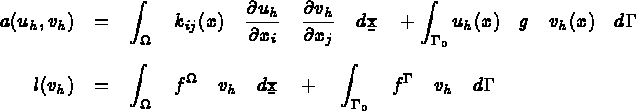
en pratique une formule de quadrature est nécessaire. Alors, 3.2 est remplacée par :
avec
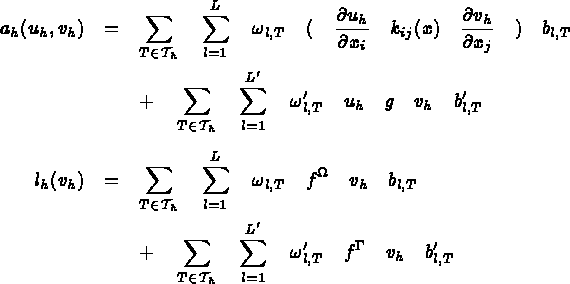
où (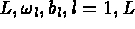 ) respectivement
(
) respectivement
(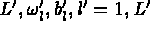 )
désigne la formule d'intégration numérique sur T et
)
désigne la formule d'intégration numérique sur T et 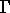 .
.
L'inconnue primordiale n'est plus la température mais le gradient de chaleur.
Soient
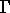
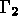 , la partie de
, la partie de 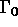 , support des conditions aux
limites de type Neumann, ie
, support des conditions aux
limites de type Neumann, ie
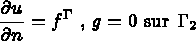
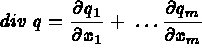
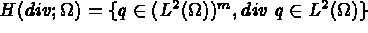
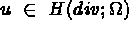 , sa trace appartient à
, sa trace appartient à
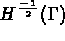
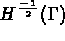 et
et 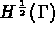
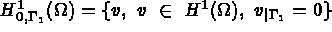
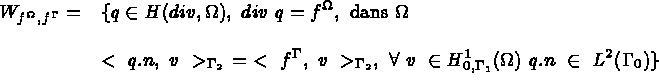
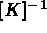 est l'inverse de la matrice de conductivité
est l'inverse de la matrice de conductivité
On recherche (p=grad u) tel que
Sous certaines conditions de régularité, la solution p=grad u de 3.4 est solution de 3.1 et réciproquement.
Trouver (p = grad u, u ) tel que
où
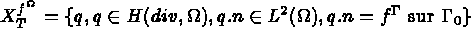
et a(.,.) et b(.,.) sont des formes
bilinéaires définies respectivement dans 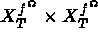 et
et 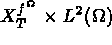 par
par
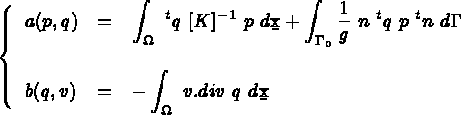
Sous certaines conditions de régularité, la solution (p, u) de 3.5 est solution de 3.1 et réciproquement.
Exemples : TETR M3T1, TRIA MT10, QUAD MQ10, TRIA MT21, QUAD MQ21, HEXA M3H1
Soient
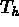 une triangulation du domaine
une triangulation du domaine 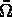 .
.
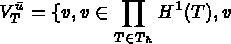 continu
aux inter-éléments de
continu
aux inter-éléments de 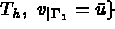
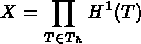
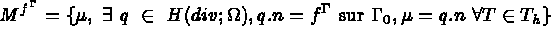
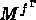 est un sous-espace de
est un sous-espace de 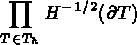
Trouver 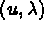 tels que
tels que
Sous certaines conditions de régularité, la solution 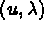 de 3.6 est solution
de 3.1 et réciproquement.
de 3.6 est solution
de 3.1 et réciproquement.
Exemples : TRIA HT10
Soient
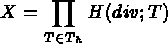
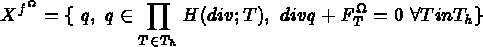
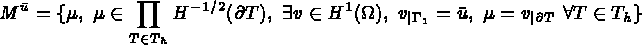
Trouver 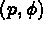 tel que :
tel que :
avec
Sous certaines conditions de régularité, la solution 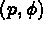 de 3.7 est solution
de 3.1 et réciproquement.
de 3.7 est solution
de 3.1 et réciproquement.
Exemples : TRI2 THD2
Soient
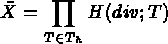
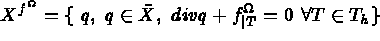
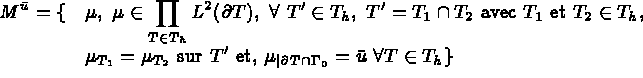
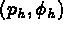 vérifiant :
vérifiant :
où a(.,.), b(.,.) et d(.,.) sont définies dans 3.8
Sous certaines conditions de régularité, la solution 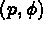 de 3.9 est solution
de 3.1 et réciproquement.
de 3.9 est solution
de 3.1 et réciproquement.
Par rapport à la formulation hybride
duale( 3.7) où 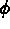 est la
trace d'une fonction de
est la
trace d'une fonction de 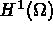 donc dans
donc dans 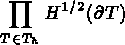 , cette contrainte de
continuité a été diminuée à
, cette contrainte de
continuité a été diminuée à 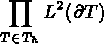 et une continuité sur chaque
arête extrémités non comprises.
et une continuité sur chaque
arête extrémités non comprises.
Exemples : TRI2 TEQ2
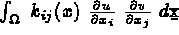 ,
,
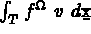 ...
... Dans tout ce qui suit, on considère le cas d'une formulation en température, sans tenir compte des effets des déformations d'origine élastique initiales. L'indice h est ignoré.
Le problème à résoudre s'écrit donc :
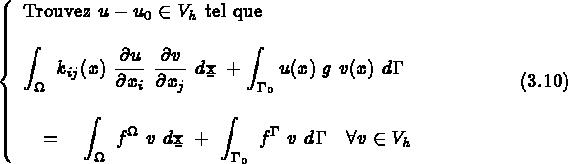
Soient 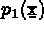 ,
, 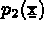 , ...,
, ..., 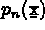 les
les 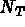 polynômes de base. On note
polynômes de base. On note

Alors,
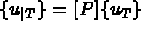
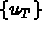 la restriction à T de { u }, valeurs
de la fonction u aux noeuds de l'élément T.
la restriction à T de { u }, valeurs
de la fonction u aux noeuds de l'élément T. Ensuite, on note
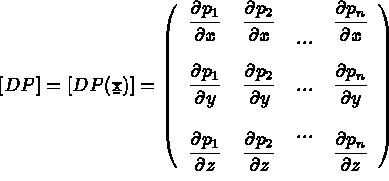
De même, on exprime 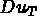 en fonction de
[ D P] et de
en fonction de
[ D P] et de 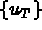 par
par
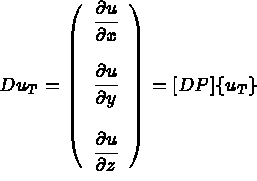
Avec pour matrice de conductivité (donnée sous sa forme générale):
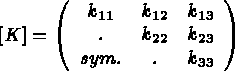
Avec ces notations on peut écrire
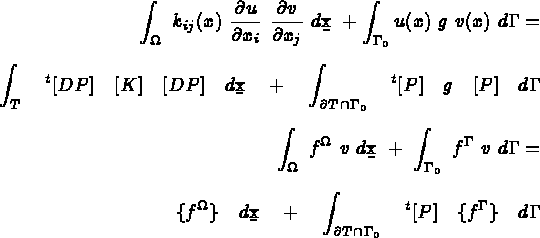
Pour chaque élément, on appelle :
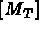 la matrice élémentaire de masse, soit
la matrice élémentaire de masse, soit

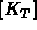 la matrice élémentaire de rigidité, soit
la matrice élémentaire de rigidité, soit
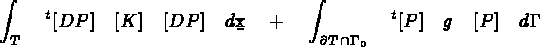
 le second membre élémentaire, soit
le second membre élémentaire, soit
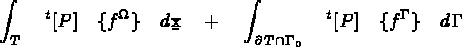
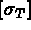 les flux élémentaires, soient
les flux élémentaires, soient
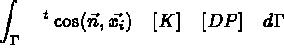
Pour obtenir le système à résoudre, il suffit de construire les matrices et seconds
membres globaux qui s'écrivent, en notant 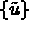 le vecteur des
degrés de liberté, regroupés noeuds par noeuds, comme:
le vecteur des
degrés de liberté, regroupés noeuds par noeuds, comme:
Trouver 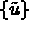 vérifiant
vérifiant
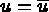 sur
sur 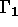
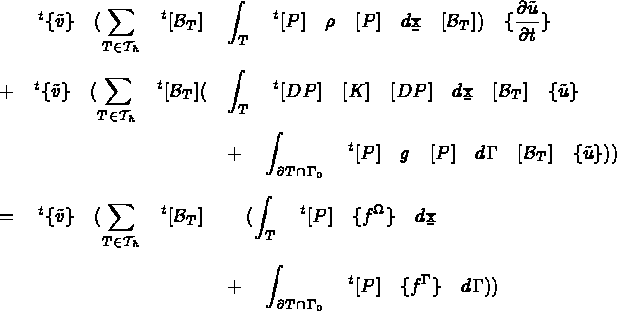
pour tout 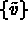 tel que v= 0 sur
tel que v= 0 sur 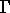
avec 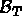 la matrice permettant de passer de la numérotation locale à la numérotation
globale i.e.
la matrice permettant de passer de la numérotation locale à la numérotation
globale i.e. 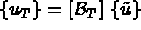 . L'opération
correspondante représente la phase d'assemblage; elle s'écrit, dans le cas de
la matrice de rigidité par exemple, comme:
. L'opération
correspondante représente la phase d'assemblage; elle s'écrit, dans le cas de
la matrice de rigidité par exemple, comme:
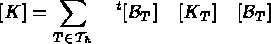
Le système ainsi obtenu peut être résolu par une méthode directe ou itérative (cf [Guide Modulef - 5]).